3.3 Построение профиля кулачковой шайбы

Предполагаем, что кулачок вращается противоположно вращению часовой стрелки. Все построения ведем в масштабе µ_s, в котором отложены ординаты на диаграмме s – φ. На

произвольной прямой OF откладываем отрезок OB₀ расстояние d в масштабе µ_s. Из точек O

и B₀ соответственно дугами радиусов r₀ и l засекаем точку A₀ – положение точки А

толкателя, самое близкое к центру кулачка. От прямой B₀A₀ откладываем угол β_max и засекаем его сторону B₀D₀ в точке D₀ дугой A₀E радиуса l. Дуга A0D0 является траекторией точки А, а длина её – ходом h толкателя. Размечаем траекторию точки А в соответствии с законом изменения ординат диаграммы s – φ, для чего откладываем точки А₀ дуги, равные ординатам этой диаграммы.

Для построения последовательных положений (A₁’; A₂’ и т.д.) точки А толкателя в обращенном движении поступаем следующим образом:

1. строим окружность радиуса 0C₀;

2. откладываем от прямой 0C₀ в направлении, противоположном вращению кулачка, заданные фазовые углы и получаем точки пересечения сторон этих углов с окружностью радиуса 0C₀;

3. Дуги C₀C₈ и C_8’C₁₆, соответствующие углам , делим на части в соответствии с делениями оси абсцисс диаграммы s – φ.

4. проводим из точек С₁; С₂ и т.д. касательные к окружности радиуса е;

5. засекаем касательные дугами окружностей радиусов OA₁; 0A₂ и т.д. в точках А₁^’; А₂^’ и т.д.

Соединяя плавной кривой точки А₀; А₁’; А₂’ и т.д. получим теоретический профиль кулачка .

Для устранения самопересечения профиля кулачка, а также из конструктивных соображений длина r радиуса ролика должна удовлетворять двум условиям r<(0,4÷0,5)r₀ и r<0,8ρ_min, где ρ_min – минимальный радиус кривизны профиля кулачка.

r<(0,4÷0,5)r₀

r<(0,4÷0,5)*31,72=15,86 мм

r<0,8ρ_min

r<0,8*32,78=26,224 мм

4. Зубчатый редуктор

4.1 Построение схемы редуктора в масштабе

№ колеса	Число зубьев, zi	Модуль зуба m, мм	Угловая скорость колеса ω1, с-1	Радиус колеса, Ri,мм
1	22	2	320	22
2	45			45
2’	14			14
3	26			26
3’	17			17
4	31			31
4’	20			20
5	64			64

4.2 Определение передаточного отношения методом картин скоростей

Находим скорость точки Р

Масштабный коэффициент картин скоростей

Расчёт передаточного отношения

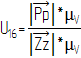
4.3 Определение передаточного отношения по формуле

Определяем передаточное отношение планетарного механизма Давида

U_3’6⁽⁵⁾=1-U_3’5^(Н)

U_3’6⁽⁵⁾

Передаточное отношение редуктора

U=U₁₂*U_32’*U_р

U=2,045*(-1,857)*4,763=-18,087

Сравнительный анализ:

4.4 Определение времени торможения (разгона)

Время разгона

Список литератур ы

1. Курсовое проектирование по теории механизмов и машин. Кореняко А. С. И др. “Вища школа”, 1970, 332 стр.

2. Артоболевский И. И. Теория механизмов и машин: Учеб. для втузов. – 4-е изд., перераб. И доп. – М.: Наука. Гл. ред. физ.-мат. лит., 1988. – 640 с.

3. Теория механизмов и машин: конспект лекций для студентов техн. спец. всех форм обучения / сост.: А.А. Балахнина, Э.Н Хенкина. – Тольятти : ТГУ, 2008. – 184 с.