Билет 4. Равноускоренное прямолинейное движение

Равноускоренное прямолинейное движение — это движение, при котором скорость тела за любые равные промежутки времени изменяется одинаково, т. е. это движение с постоянным по модулю и направлению ускорением.

— уравнение ускорения.

По определению ускорения .

Пусть в момент времени t₀ = 0 скорость тела равна , в момент времени t — . Тогда за промежуток времени скорость изменилась на Следовательно, ускорение

— уравнение скорости.

Или в проекциях: .

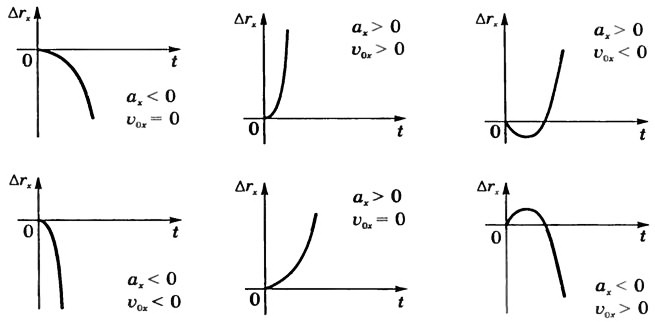
Эти зависимости кинематических величин от времени изобразим графически для трех тел (рис. 1).

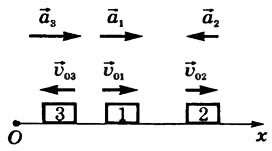
Рис. 1

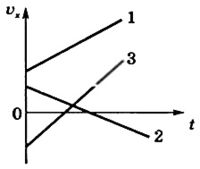
Графики ускорения a_x = f(t) представлены на рисунке 2, а графики скорости υ_x = f(t) — на рисунке 3.

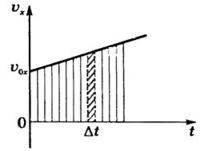
Для нахождения перемещения воспользуемся графиком скорости (рис. 4).

Рис. 2

Рис. 3

Рис. 4

Для малого промежутка времени Δt изменением величины скорости можно пренебречь и скорость можно считать постоянной. Тогда перемещение за промежуток времени Δt будет равно площади узкой густо заштрихованной полоски. Мысленно разбив все время движения тела на малые промежутки времени и найдя перемещение за каждый отдельный промежуток времени, суммируем эти перемещения. Модуль проекции перемещения за промежуток времени в пределе численно равен площади заштрихованной трапеции.

Следовательно,

Подставив значение в (1), получим:

— уравнение перемещения в проекциях;

— уравнение перемещения в векторном виде.

Учитывая, что , имеем:

— кинематическое уравнение равноускоренного движения.

Его векторный вид: .

Исключая из уравнений скорости и перемещения время t, получим:

Сравнивая выражение (1) с формулой , найдем:

— проекция средней скорости при равноускоренном движении.

Графиком перемещения является парабола, положение вершины которой зависит от направлений начальной скорости и ускорения (

2.Закон Ома для полной цепи:

, (2)

где:

• — ЭДС источника напряжения(В),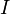

• — сила тока в цепи (А),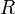

• — сопротивление всех внешних элементов цепи(Ом) ,

• — внутреннее сопротивление источника напряжения(Ом) .

Из Закона Ома для полной цепи вытекают следствия:

• При r<<R Сила тока в цепи обратно пропорциональна её сопротивлению. А сам источник в ряде случаев может быть назван источником напряжения

• При r>>R Сила тока от свойств внешней цепи (от величины нагрузки) не зависит. И источник может быть назван источником тока.

(3)

(где есть напряжение или падение напряжения, или, что то же, разность потенциалов между началом и концом участка проводника) тоже называют «Законом Ома».

(4)

То есть сумма падений напряжения на внутреннем сопротивлении источника тока и на внешней цепи равна ЭДС источника. Последний член в этом равенстве специалисты называют «напряжением на зажимах», поскольку именно его показывает вольтметр, измеряющий напряжение источника между началом и концом присоединённой к нему замкнутой цепи. В таком случае оно всегда меньше ЭДС.

(5)

Применима другая формулировка:

Сила тока в участке цепи прямо пропорциональна напряжению и обратно пропорциональна электрическому сопротивлению данного участка цепи.

Выражение (5) можно переписать в виде:

(6)

где коэффициент пропорциональности G назван проводимость или электропроводность. Билет 5.

Среди различных видов криволинейного движения особый интерес представляет равномерное движение тела по окружности. Это самый простой вид криволинейного движения. Вместе с тем любое сложное криволинейное движение тела на достаточно малом участке его траектории можно приближенно рассматривать как равномерное движение по окружности.

Центростремительное ускорение. При равномерном движении по окружности значение скорости остается постоянным, а направление вектора скорости изменяется в процессе движения. Определим ускорение тела, движущегося равномерно по окружности радиусом R. За интервал времени Δtтело проходит путь .

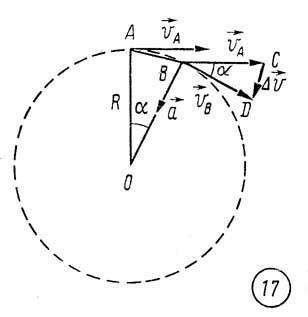
Этот путь Δsравен длине дуги АВ (рис. 17). Векторы скоростей и точках А и В направлены по касательным к окружности в этих точках, угол α между векторами и равен углу между радиусами ОА и OB.

Для нахождения вектора ускорения нужно найти разность векторов скорости и определить отношение изменения скорости к малому интервалу времени Δt, за который произошло это изменение:

.

Из подобия треугольников ОАВ и BCD следует

.(3.1)

Если интервал времени Δt мал, то мал и угол α. При малых значениях угла α длина хорды АВ примерно равна длине дуги АВ, т. е. . Так как , и , то из выражения (3.1) получаем

,(3.2)

. (3.3)

Поскольку

, (3.4)

из выражений (3.3) и (3.4) получаем

. (3.5)

Из рисунка 17 видно, что, чем меньше угол α, тем ближе направление вектора к направлению на центр окружности. Так как вектор ускорения равен отношению вектора к интервалу времени Δtпри условии, что интервал времени Δtочень мал, то вектор ускорения при равномерном движении по окружности направлен к ее центру.

При изменении положения тела на окружности меняется направление на центр окружности. Следовательно, при равномерном движении тела по окружности модуль ускорения имеет постоянное значение, но направление вектора ускорения изменяется со временем. Ускорение при равномерном движении по окружности называется центростремительным ускорением.

Криволинейные движения – движения, траектории которых представляют собой не прямые, а кривые линии. По криволинейным траекториям движутся планеты, воды рек.

Криволинейное движение – это всегда движение с ускорением, даже если по модулю скорость постоянна. Криволинейное движение с постоянным ускорением всегда происходит в той плоскости, в которой находятся векторы ускорения и начальные скорости точки. В случае криволинейного движения с постоянным ускорением в плоскости xOy проекции v_xи v_y ее скорости на оси Ox и Oy и координаты x и y точки в любой момент времени tопределяется по формулам

Частным случаем криволинейного движения – является движение по окружности. Движение по окружности, даже равномерное, всегда есть движение ускоренное: модуль скорости все время направлен по касательной к траектории, постоянно меняет направление, поэтому движение по окружности всегда происходит с центростремительным ускорением где r – радиус окружности.

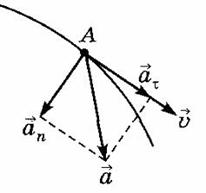
Вектор ускорения при движении по окружности направлен к центру окружности и перпендикулярно вектору скорости.

При криволинейном движении ускорение можно представить как сумму нормальной и тангенциальной составляющих:

,

- нормальное (центростремительное) ускорение, направлено к центру кривизны траектории и характеризует изменение скорости по направлению:

v – мгновенное значение скорости, r – радиус кривизна траектории в данной точке.

- тангенциальное (касательное) ускорение, направлено по касательной к траектории и характеризует изменение скорости по модулю.

Полное ускорение, с которым движется материальная точка, равно:

.

Кроме центростремительного ускорения, важнейшими характе­ристиками равномерного движения по окружности являются период и частота обращения.

.

ОПРЕДЕЛЕНИЕ ВЕЛИЧИНЫ (СИЛЫ) ТОКА _{<!--[if !vml]--> <!--[endif]-->}.

ЗАКОН ОМА ДЛЯ УЧАСТКА ЦЕПИ: величина (сила) тока, текущего по однородному (в смысле отсутствия сторонних сил) металлическому проводнику, пропорциональна падению напряжения U на проводнике _{<!--[if !vml]--> <!--[endif]-->}, где R - сопротивление проводника.

РЕЗИСТОРОМ называется устройство, обладающее заданным постоянным сопротивлением.

НАПРЯЖЕНИЕ НА РЕЗИСТОРЕ _{<!--[if !vml]--> <!--[endif]-->}.

ЗАКОН ОМА ДЛЯ НЕОДНОРОДНОГО УЧАСТКА ЦЕПИ

_{<!--[if !vml]--> <!--[endif]-->}, где j₁ и j₂ - потенциалы концов участка Е₁₂ - э.д.с., действующая на данном участке цепи.

ЗАКОН ОМА ДЛЯ ЗАМКНУТОЙ ЦЕПИ _{<!--[if !vml]--> <!--[endif]-->}, где Е - суммарная э.д.с., действующая в цепи, R - суммарное сопротивление всей цепи.

РАЗВЕТВЛЕННОЙ ЦЕПЬЮ называется электрическая цепь, имеющая узлы.

УЗЛОМ называется точка, в которой сходится более чем два проводника. Ток, текущий к узлу, принято считать положительным, а ток, текущий от узла, считается отрицательным.

ПЕРВОЕ ПРАВИЛО КИРХГОФА: алгебраическая сумма токов, сходящихся в узле, равна нулю _{<!--[if !vml]--> <!--[endif]-->} = 0.

ВТОРОЕ ПРАВИЛО КИРХГОФА: в каждом из замкнутых контуров, которые можно мысленно выделить в данной разветвленной цепи, алгебраическая сумма падений напряжения равна алгебраической сумме э.д.с.

_{<!--[if !vml]--> <!--[endif]-->}.

При анализе разветвленной цепи следует обозначать с одним индексом ток, протекающий по всем последовательно соединенным элементам от одного узла до другого. Направление каждого тока выбирается произвольно.

При составлении уравнений второго правила Кирхгофа токам и э.д.с. нужно приписывать знаки в соответствии с выбранным (как вам удобно) направлением обхода:

<!--[if !supportLists]--><!--[endif]-->ток принято считать положительным, если он совпадает с направлением обхода, и отрицательным, если он направлен против этого направления;

<!--[if !supportLists]--><!--[endif]-->э.д.с. считается положительной, если ее действие (создаваемый ею ток) совпадает с направлением обхода.

Количество уравнений первого правила Кирхгофа должно быть на одно меньше количества узлов в данной цепи. Количество независимых уравнений второго правила Кирхгофа должно быть таким, чтобы общее количество уравнений оказалось равным количеству различных токов. Каждый новый контур при этом должен содержать хотя бы один участок цепи, не вошедший в уже рассмотренные контуры.

Для упрощения расчетов сложных электрических цепей, содержащих неоднородные участки, используются правила Кирхгофа, которые являются обобщением закона Ома на случай разветвленных цепей.

В разветвленных цепях можно выделить узловые точки (узлы), в которых сходятся не менее трех проводников (рис. 1.10.1). Токи, втекающие в узел, принято считать положительными; вытекающие из узла – отрицательными.

Рисунок 1.10.1. Узел электрической цепи. I1, I2 > 0; I3, I4 < 0

В узлах цепи постоянного тока не может происходить накопление зарядов. Отсюда следует первое правило Кирхгофа:

Алгебраическая сумма сил токов для каждого узла в разветвленной цепи равна нулю:

I1 + I2 + I3 + ... + In = 0.

Первое правило Кирхгофа является следствием закона сохранения электрического заряда.

В разветвленной цепи всегда можно выделить некоторое количество замкнутых путей, состоящих из однородных и неоднородных участков. Такие замкнутые пути называются контурами. На разных участках выделенного контура могут протекать различные токи. представлен простой пример разветвленной цепи. Цепь содержит два узла a и d, в которых сходятся одинаковые токи; поэтому только один из узлов является независимым (a или d).

Второе правило Кирхгофа является следствием обобщенного закона Ома.

Запишем обобщенный закон Ома для участков, составляющих один из контуров цепи, , Для этого на каждом участке нужно задать положительное направление тока и положительное направление обхода контура. При записи обобщенного закона Ома для каждого из участков необходимо соблюдать определенные «правила знаков»,

Для участков контура abcd обобщенный закон Ома записывается в виде:

Для участка bc: I₁R₁ = Δφ_bc – ₁.

Для участка da: I₂R₂ = Δφ_da – ₂.

Складывая левые и правые части этих равенств и принимая во внимание, что Δφ_bc = – Δφ_da , получим:

I1R1 + I2R2 = Δφbc + Δφda – 1 + 2 = – 1 – 2.

Аналогично, для контура adef можно записать:

– I2R2 + I3R3 = 2 + 3.

Второе правило Кирхгофа можно сформулировать так: алгебраическая сумма произведений сопротивления каждого из участков любого замкнутого контура разветвленной цепи постоянного тока на силу тока на этом участке равна алгебраической сумме ЭДС вдоль этого контура.

Первое и второе правила Кирхгофа, записанные для всех независимых узлов и контуров разветвленной цепи, дают в совокупности необходимое и достаточное число алгебраических уравнений для расчета значений напряжений и сил токов в электрической цепи. Для цепи, изображенной на рис. 1.10.2, система уравнений для определения трех неизвестных токов I₁, I₂ и I₃ имеет вид:

I1R1 + I2R2 = – 1 – 2,

– I2R2 + I3R3 = 2 + 3,

– I1 + I2 + I3 = 0.

Таким образом, правила Кирхгофа сводят расчет разветвленной электрической цепи к решению системы линейных алгебраических уравнений. Это решение не вызывает принципиальных затруднений, однако, бывает весьма громоздким даже в случае достаточно простых цепей. Если в результате решения сила тока на каком-то участке оказывается отрицательной, то это означает, что ток на этом участке идет в направлении, противоположном выбранному положительному направлению.

Билет 62.Прямолинейное равноускоренное (равнопеременное) движение (равноускоренное или равнозамедленное):

a_t = a = const, a_n = 0, кинематические уравнения этого движения v = v_o ± at, s = vdt = (v_o ± at)dt = v_ot ± at²/2,

здесь v_o - скорость в начальный момент времени.

1.3.3.Равноускоренное (равнопеременное) движение по окружности (для пространственной траектории - по спирали): a_t = const, a_n = сonst; из формулы a_n=v²/r следует, что радиус кривизны траектории постоянен, т.е. имеет место движение по окружности.

Для описания движения по окружности вводят понятие угловой скорости (векторная величина)

При равномерном движении т. М по окружности (рис. 33):

– модуль скорости не изменяется | ₁| = | ₂| v _t = 0 ;

– направление вектора скорости изменяется _n = 0 .

Рис. 33

Полное ускорение в этом движении (§ 6, 2а) равно нормальному ускорению (или центростремительному): = _n и направлено перпендикулярно к направлению вектора скорости , по радиусу к центру окружности. При этом движении радиусвектор т. М поворачивается на угол = – ₀ за интервал времени t = t – t₀, а его конец описывает дугу окружности .

При вращении угол поворота изменяется с течением времени, тогда уравнение = (t) – это уравнение вращения. Угол (или ) аналогичен величине линейного пути S при поступательном движении, и его называют углом поворота или угловым путем. Элементарное угловое перемещение – это вектор, направленный вдоль оси по правилу правого винта и численно равный углу (рис. 34). Введем угловые кинематические характеристики: угловую скорость и угловое ускорение при вращении вокруг неподвижной оси (§ 1, рис. 3).

Угловая скорость

Средняя угловая скорость _cp – это физическая величина, равная отношению угла поворота к интервалу времени, за который оно произошло.

. (32)

Единицы угловой скорости в СИ и в системе СГС

.

Мгновенная угловая скорость _мгн – это физическая величина, равная пределу отношения углового перемещения к интервалу времени, за который оно произошло (при t 0).

. (33)

Угловая скорость – производная от угла поворота по времени.

При равномерном движении по окружности вокруг закрепленной оси, при котором за любые равные промежутки времени радиус-вектор точки поворачивается на одинаковые углы, угловая скорость может рассматриваться как скаляр:

.

_cpмгн = const

; . (34)

При равномерном вращении модуль угловой скорости: .

Угловой путь: = w t.

Из формулы (34) следует уравнение равномерного движения материальной точки по окружности:

. (35)

или

.

Направление вектора определяется по правилу буравчика (или правого винта): направление вращения буравчика, расположенного перпендикулярно плоскости вращения, совпадает с движением т. М по окружности, а его поступательное движение вдоль оси совпадает с направлением угловой скорости (рис. 34).

Рис. 34

Угловое ускорение

Среднее угловое ускорение _cp – это физическая величина, равная отношению изменения вектора угловой скорости к интервалу времени, за который оно произошло.

. (36) Мгновенное угловое ускорение – это физиче-ская величина, равная пределу отношения изменения угловой скорости к интервалу времени, за который оно произошло (при t 0).

; . (37)

Угловое ускорение – производная от угловой скорости по времени или вторая производная от угла поворота по времени:

; .

При равномерном движении по окружности

= 0. Равномерное движение точки по окружности – это периодическое движение.

Период Т – это время одного полного оборота.

Частота вращения v – это физическая величина, обратная периоду, и характеризует число полных оборотов за единицу времени.

где N – число полных оборотов за единицу времени.

Линейная скорость (мгновенная скорость при движении по окружности):

.

При t = Т, S = 2 R

, v = 2 Rv. (39)

Угловая скорость при t = Т равна:

.

Угловой путь при равномерном движении материальной точки по окружности:

.

Уравнение равномерного движения материальной точки по окружности:

При t = Т, = 2p

, w = 2 v. (40)

Связь линейной и угловой скорости

Из формул (39) и (40) следует, что

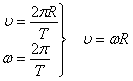. (41)

Связь тангенциального ускорения а_t и углового ускорения

а_t = R. (42)

Примечание. Угловая скорость и угловое ускорение – векторные величины. Направления векторов угловой скорости и углового ускорения перпендикулярны плоскости окружности (рис. 34). Вектор мгновенной скорости материальной точки при движении по окружности связан с вектором угловой скорости по правилу векторного произведения

Формула нормального ускорения (вывод)

Рассмотрим равномерное движение по окружности:| ₁| = | ₂| v (рис. 35). Перенесем вектор в точку В и построим вектор – изменение скорости за время t. Треугольники BCD и OAB подобны как равнобедренные с одинаковыми углами при вершинах. Поэтому:

или .

При t 0 угол между ₁ и ₂ стремится к нулю ( 0), а угол между ₂ и – к прямому. Значит, направление вектора и ( ) приближается к направлению нормали к траектории, т.е. к направлению радиуса. Следовательно, ускорение – нормальное (центростремительное):

, где .

Учитывая, что при t 0 длина хорды АВ приближается к длине дуги S, получим:

,

и формула нормального ускорения:

или (41): (43) Угловое ускорение — показывает, на сколько изменилась угловая скорость за единицу времени, и, по аналогии с линейным ускорением, равно:

Направление вектора здесь показывает, увеличивается или уменьшается модуль скорости. Если векторы углового ускорения и скорости сонаправлены, значение скорости растёт, и наоборот.

Формулы равномерного движения материальной точки по окружности