Индивидуальное задание вариант 25 / toe2(3_4)-025

File: ;

Created 18.10.2002 by Max Shonichev; Last edited 18.12.02 by Max Shonichev

Отчет о выполнении домашнего задания.

Шоничев М.А.

Расчет переходных процессов в цепях первого порядка во временной области при постоянных воздействиях. Вариант 25.

2.3. При t=0 в цепи замыкается ключ. Найти независимые начальные условия, составить уравнения состояния. Для t>0 найти u_C и i_L, использовав аналитическое решение уравнений состояния, а также численное - по методу Эйлера.

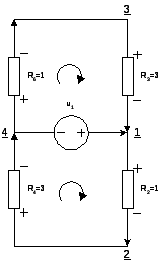
Цепь: 116 – u₁=8, 212 – R₂=2, 323 – К замыкается, 434 – L₄=4, 546 – R₅=6, 635 – C₆=1, 756 – u₇=4.

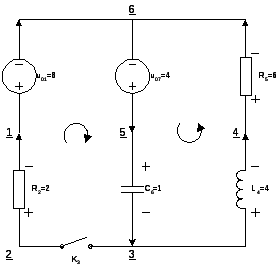
1. н.н.у. i_L(0_-)=0, u_C(0_-)=4.

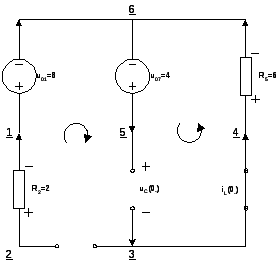
2. t>0. Нарисуем граф цепи и построим по нему главные контуры и главные сечения.

Гк1: 1-6-5-3-1: u01 - u07 + uC + u2 = 0 Гк2: 6-5-3-4-6: -u07 + uC + uL + u5 = 0 Гс1: 2,6,4: i2 + iL4 = iC6 Гс2: 2,7,4: i2 + iL4 = i7 Гс3: 2,1: i2 = i1 Гс4: 4,5: iL4 = i5

Теперь построим уравнения состояния.

i_L' = u_L/L, u_C' = i_C/C

u_L = u₀₇ - u_C - u₅ = u₀₇ - u_C - R₅*i₅ = u₀₇ - u_C - R₅*i_L

i_C = i₂ + i_L = u₂/R₂ + i_L = i_L + (u₀₇ - u_C - u₀₁)/R₂

Итак, в матричной форме:

= [A] * + [B] * uC'		uC		u01
iL'		iL		u07

где [A] = = -1/C6R2	1/C6		-1/2	1
-1/L4	-R5/L4		-1/4	-3/2

[B] = = -1/C6R2	1/C6R2		-1/2	1/2
0	1/L4		0	1/4

3. Для нахождения частот собственных колебаний, найдем корни характеристического полинома: det([A]-p[E]) = 0.

det = (p + 1/2)(p + 3/2) + 1/4 = p2 + 2p + 1 = (p+1)2 -1/2 - p	1
-1/4	-3/2 - p

Корни: p_1,2 = -1, вещественные отрицательные кратные, то есть имеет место критический режим.

свободные составляющие решения:

u_Ссв(t) = A₁e^p1t + tA₂e^p2t

i_Lсв(t) = B₁e^p1t + tB₂e^p2t

4. t=. Вынужденные составляющие переменных состояния определим, подставив в уравнения u_C' = i_L' = 0, так как при t= - в цепи установившийся режим при постоянных воздействиях.

* = + * 0		-1/2	1		uCу		-1/2	1/2		u01
0		-1/4	-3/2		iLу		0	1/4		u07

= -1/2	1		uCу		2
-1/4	-3/2		iLу		-1

u_Cу=-2, i_Lу=1.

Общее решение:

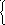u_С(t) = A₁e^-t + tA₂e^-t - 2

i_L(t) = B₁e^-t + tB₂e^-t + 1

5. t=0₊. Определяем произвольные постоянные A₁, A₂, B₁, B₂ исходя из начальных условий и уравнений состояния:

u_C(0₊) = u_C(0_-) = 4, i_L(0₊) = i_L(0_-) = 0.

* = + * uC'(0+)		-1/2	1		uC(0+)		-1/2	1/2		u01
iL'(0+)		-1/4	-3/2		iL(0+)		0	1/4		u07

u_C'(0₊) = (-1/2)*4 + (-1/2)*8 + (1/2)*4 = -4

i_L'(0₊) = (-1/4)*4 + (1/4)*4 = 0

u_C(0₊) = A₁e^-t + tA₂e^-t - 2 = A₁ - 2 = 4, откуда A₁=6

i_L(0₊) = B₁e^-t + tB₂e^-t +1 = B₁ + 1 = 0, откуда B₁=-1

u_L'(0₊) = -A₁e^-t + A₂e^-t - tA₂e^-t = -A₁ + A₂ = -4, откуда A₂=2

i_L'(0₊) = -B₁e^-t + B₂e^-t - tB₂e^-t = -B₁ + B₂ = 0, откуда B₂=-1

7. Итак, решение: u_C(t) = 6e^-t + 2t*e^-t - 2

i_L(t) = -e^-t - t*e^-t + 1

Произведем расчет уравнений состояния по методу Эйлера.

Шаг численного расчета выберем так, чтобы минимальной постоянной времени соответствовало хотя бы 5 шагов расчета. = 3, = 0.067

u_C' = -u_C/2 + i_L - 2

i_L' = -u_C/4 - 3i_L/2 + 1

u_C(0_-)=4, i_L(0_-)=0 принимаем за данные нулевого шага.

t₁ = 0.067

u_C1 = u_C0 + u_C1' = u_C0 + ( -u_C0/2 + i_L0 - 2) = 4 + 0.067 * (-4/2 + 0 - 2) = 3.732

i_L1 = i_L0 + i_L1' = i_L0 + ( -u_C0/4 - 3i_L0/2 + 1) = 0 + 0.067 * (-4/4 - 3*0/2 + 1) = 0

t₂ = 0.134

u_C2 = u_C1 + u_C2' = u_C1 + ( -u_C1/2 + i_L1 - 2) = 3.732+0.067*(-3.732/2+0-2) = 3.473

i_L2 = i_L1 + i_L2' = i_L1 + ( -u_C1/4 - 3i_L1/2 + 1) = 0+0.067*(-3.732/4-3*0/2+1) = 0.0045

t₃ = 0.201

u_C3 = u_C2+u_C3' = u_C2+(-u_C2/2+i_L2-2) = 3.473+0.067*(-3.473/2+0.0045-2) = 3.223

i_L3 = i_L2+i_L3' = i_L2+(-u_C2/4-3i_L2/2 + 1) = 0.0045+0.067*(-3.473/4-3*0.0045/2+1) = 0.012875

t₄ = 0.268

u_C4 = 3.223 + 0.067 * ( -3.223/2 + 0.012875 - 2) = 2.982

i_L4 = 0.012875 + 0.067*( -3.223/4 - 3*0.012875/2 + 1) = 0.0246

t₅ = 0.335

u_C5 = 2.982 + 0.067 * ( -2.982/2 + 0.0246 - 2) = 2.75

i_L5 = 0.0246 + 0.067*( -2.982/4 - 3*0.0246/2 + 1) = 0.03918

t₆ = 0.402

u_C6 = 2.75+ 0.067 * ( -2.75/2 + 0.03918 - 2) = 2.5265

i_L6 = 0.03918 + 0.067*( -2.75/4 - 3*0.03918/2 + 1) = 0.05618

t₇ = 0.469

u_C7 = 2.5265 + 0.067 * ( -2.5265/2 + 0.05618 - 2) = 2.31163

i_L7 = 0.05618 + 0.067*( -2.5265/4 - 3*0.05618/2 + 1) = 0.07522

8. Построим графики переходного процесса:

= -1/p₁ = 1, время затухания = 3 = 3

На графиках отражены аналитические данные и результаты численных расчетов (жирный пунктир).

2.4. Найти h₁(t), h(t) и h₂(t) для указанной реакции f₂(t); Вычислить f₂(t) для воздействия f₁(t), заданного аналитически в вариантах задачи 2.4 и графически в виде импульса треугольной формы в соответствующих вариантах задачи 1.9.

Цепь: 115 – u₁=f₁, 212 – R₂ =1, 313 – R₃=3, 424 – R₄=3, 523 – L₅=1.5, 634 – R₆=1.

f₂=i₃.

f_1a=12 e^-2t. f_1b=3t/2 - 3, 2<=t<=4

Для расчета переходной характеристики подключим к цепи единичный источник напряжения с помощью идеального ключа.

1. t=0-. i_L(0_-)=0, i₃(0_-)=0

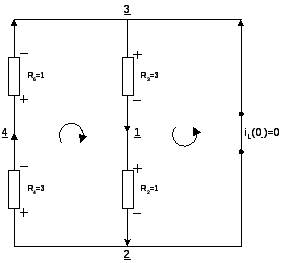
2. t=+.

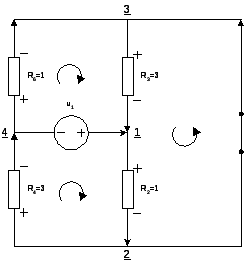
Параллельно включены R₆ и R₄, а также R₃ и R₂, причем результирующие R₆₄=R₆R₄/(R₆+R₄)=3/4 и R₂₃=R₂R₃/(R₂+R₃)=3/4 включены последовательно источнику, поэтому i₆₄=i₂₃=u₁/(R₆₄+R₂₃) = 2/3, откуда i_3у=(i₂₃*R₂₃)/R₃=1/6.

3. t=0+. На этот раз параллельно источнику подключены суммарные сопротивления R₃₆ = R₃ + R₆ и R₂₄ = R₂ + R₄.

Ток i3(0+) = i36 = u1/R36= 1/4.

4. Определяем значение . Rэ=2,=L5/Rэ=0.75

5. Общее решение:

i₃(t) = i_3у + (i₃(0₊) - i_3у)*e^-t/= 1/6 + (1/4 - 1/6)e^-t/0.75 = 1/6 + 1/12 e^-4t/3.

Переходная характеристика численно равна реакции цепи, поэтому

h₁(t) = i₃(t)(t) = (1/6 + e^-4t/3/12)*(t).

Импульсная характеристика равна производной от переходной характеристики:

h(t) = (di₃/dt)*(t) + h₁(0₊)*(t) = (-1/9)e^-4t/3(t) + (1/4)(t)

а) Найдем реакцию для воздействия заданного формулой f_1a=12 e^-2t с помощью интегралов свертки.

При >0: .

==

===.

б) Найдем реакцию для воздействия, заданного кусочно-линейной функцией методом двойного дифференцирования. f_1b=3t/2 - 3, 2<=t<=4

Вначале, для t>0 находим h₂(t)== t/6 + 1/16 - e^-4t/3/16. То есть, для любого t: h₂(t)= (t/6 + 1/16 - e^-4t/3/16)

Далее,

f ''₁(t)= 3/2-3/2, то есть f₁(t)= 3/2-3/2.

Тогда, реакция находится по принципу наложения:

f ₂(t)= 3/2 h₂(t-2) - 3/2 h₂(t-4) =*((t-2)/4 + 3/32 - 3/32e^-4(t-2)/3) - *((t-4)/4 + 3/32 - 3/32 e^{‑4(t‑4)/3}).

Для вычисления этой функции, можно вычислить первый множитель без на промежутке (2..4], а затем - разность первого множителя без и второго множителя без на промежутке (4..+).

f ₂(t)= (t/4 - 13/32 - 3/32 e^-4(t-2)/3) + (2/4 - 3/32 e^-4(t-2)/3 + 3/32 e^-4(t-4)/3)

Page 8