3. Параметри передатної функції

3.3.2.1 Перетворення Лапласа

У часовий області лінійний елемент, як правило, описується диференційним рівнянням (3.1) з постійними коефіцієнтами. Зокрема, у попередньому розділі описані розв'язки цього рівняння при дії деяких тестових сигналів при нульових початкових умовах.

Перетворення Лапласа виду

(3.7)

ставить у відповідність функцію дійсного змінного x(t) і функцію комплексного змінного X(s): , де L – оператор Лапласа (3.7), t – незалежна дійсна змінна (час) і s = σ+ jω – незалежна комплексна змінна (має зміст частоти), x(t) і X(s) називають відповідно оригіналом та зображенням за Лапласом.

Можна показати, що приведене перетворення існує для всіх реальних сигналів, які визначені при і дорівнює нулю при .

Обернене перетворення Лапласа визначає оригінал за зображенням:

, (3.8)

, де L^-1 – обернений оператор Лапласа (3.8).

Укажемо деякі основні властивості перетворення Лапласа:

а) лінійність;

полягає у виконанні дистрибутивного закону

, α, β – константи;

б) диференціювання оригінала при нульових початкових умовах

;

в) інтегрування оригіналу при нульових початкових умовах

;

г) теорема про згортку (множення зображень)

.

д) теорема розкладу (Хевісайда), що дозволяє оригінал за зображенням:

якщо - дробно-лінійна функція, яка складається з поліномів аргументів s порядку n і m, причому m < n та серед коренів рівняння немає кратних, то

де .

Розглянемо два простих приклади.

Приклад 3.1. Знайти зображення за Лапласом імпульсу Дірака .

За означенням імпульсу Дірака (3.2):

.

При = 0: . 

Приклад 3.2. Знайти зображення за Лапласом функції Хевісайда .

За властивістю в):

.

При t₀ = 0: . 

Приклад 3.3. Знайти оригінал зображення за Лапласом К/(s(1+sT)).

За теоремою розкладу д) знаходимо:

B’(s) = s²T + s; s₁ = 0, s₂ = -1/T;

x(t) = Ke^0t + Ke^-t/T = K(1 – e^-t/T).

Приклад показує, як знайти перехідну характеристику для інерційної ланки першого порядку с передатної функцією К/(1+sT). 

.

2. Передатна функція

Для отримання передатної функції перетворимо диференційне рівняння (3.1) за Лапласом при нульових початкових умовах. Враховуючи властивість лінійності (а) та множення на s при кожному взятті похідної (б) перетворення Лапласа, маємо

. (3.9)

Передатною функцією W(s) елементу автоматики називається відношення зображення за Лапласом вихідного сигналу Z(s) до зображення його вхідного сигналу Y(s), взяте при нульових початкових умовах.

Знаходячи з (3.9.) відношення Z(s)/Y(s), отримаємо

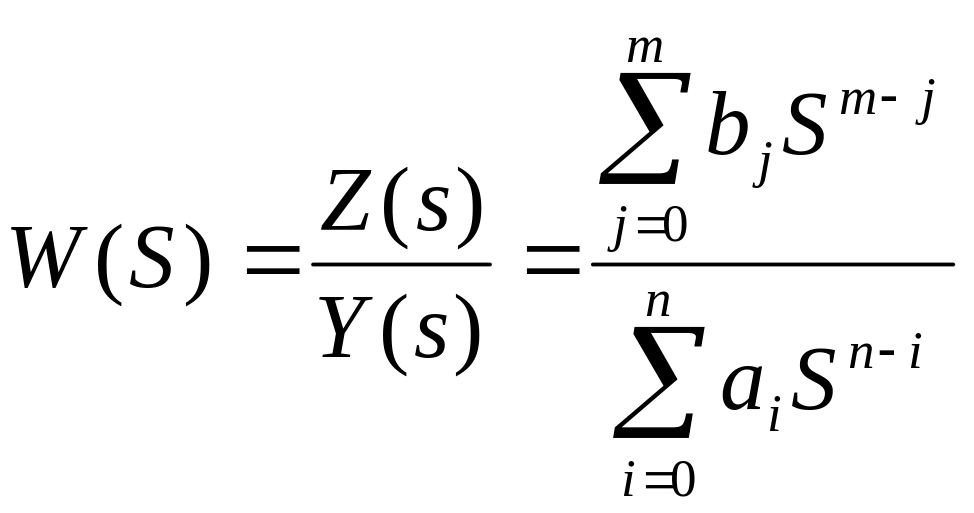. (3.10)

Таким чином, якщо передаточна функція відома, то її реакцію z(t) на будь-який вхідний сигнал y(t) можна визначити наступним шляхом:

• знаходимо зображення заданого сигналу y(t) за Лапласом: ;

• відповідно до (3.10)) знаходимо Z(s) = W(s) Y(s);

• за допомогою зворотного перетворення Лапласа знаходимо оригінал z(t) за зображенням Z(s): .

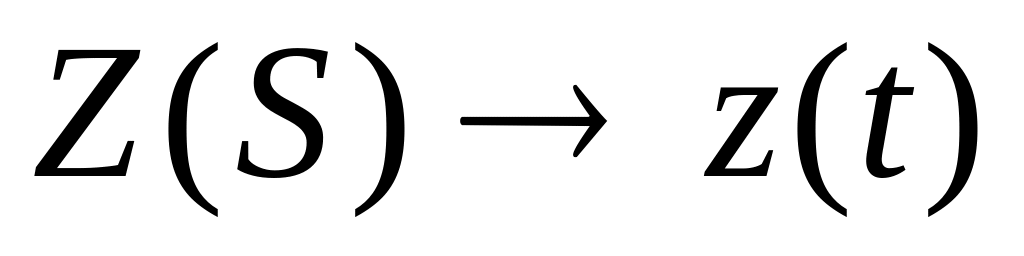Зокрема, так можна знайти імпульсну або перехідну функції елементу, якщо відома його передатна функція. Саме цей прийом був застосовний при знаходженні перехідної характеристики у прикладі 3 попереднього пункту.

Передатну функцію можна представити в іншої формі: якщо розкласти на множники поліноми чисельника та знаменника (3.10), то будемо мати:

, . (3.11)

Параметрами передатної функції (3.10) є коефіцієнти a_j, b_i, а параметрами передатної функції у формі (3.11) – її нулі n_i та її полюси p_j, причому i = 1, …, m, j = 1, …, n.

К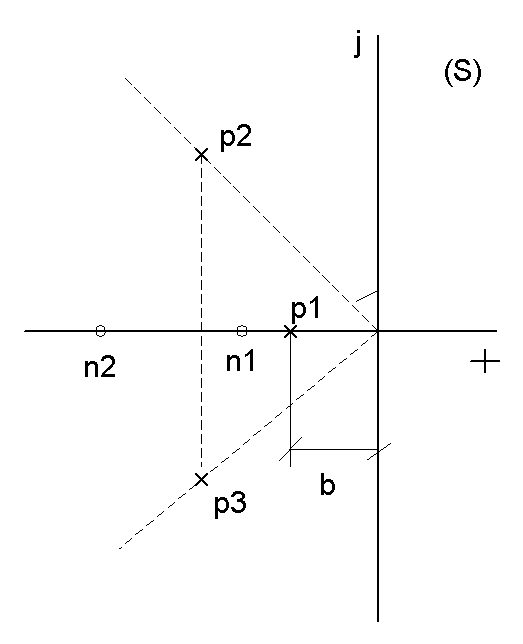 оефіцієнти (3.10) мають різну розмірність, як правило, вони позбавлені фізичного сенсу. Нулі же і полюси мають однакову розмірність частоти, як і комплексна незалежна s. Це дає можливість розташувати всі нулі та полюси на комплексній площині (s). Отримана таким чином карта розташування нулів та полюсів несе багато інформації про елемент, що описується. Приклад цієї карти зображений на рисунку 3.6.

Рисунок 3.6 – Карта розташування нулів та полюсів

Конкретний вигляд карти, зображеної на рисунку 3.6, дозволяє зробити декілька висновків відносно властивостей відповідного елемента:

• система описується диференційним рівнянням 3-го порядку, оскільки має три полюси p1, p2, p3;

• система є стійкою, бо всі три її полюси розташовані у лівій частини комплексної площини (s);

• система є мінімально-фазової, оскільки не тільки полюси, але і її нулі n1, n2 лежать у лівій частині комплексної площини (s); це означає, що властивості системи повністю визначаються одною (а не двома) дійсною частотною характеристикою; така перевага обговорюється детально у наступному пункті;

• ступінь (запас) стійкості системи складає b; ця ж величина дозволяє оцінити нижню границю швидкодії – найбільш повільна складова перехідного процесу досягає 5-відсоткової зони навколо встановленого стану приблизно за час 3/b;

• параметр коливальності перехідного процесу складає Ctgβ.

Таким чином, карта розподілу полюсів та нулів несе багато інформації про динамічні властивості елемента. Вона може також використовуватись для синтезу динамічних систем [6].

Важливою особливістю коефіцієнтів диференційного рівняння (3.1) і передатної функції (3.10) є те, що вони дозволяють багатьма способами перейти до опису елементу у просторі станів:

du/dt =Au + By;

z = Cu, (3.12)

де u – вектор стану, y – вектор входу, z – вектор виходу;

A, B, C – матриці.

Позначення у системі рівнянь (3.12) відповідають рисунку 3.1, хоча вхід і вихід лінійного елементу представлені тепер векторами, координати яких є функціями часу t, а вектор стану на цьому рисунку не показаний.

Матриці A, B, C вичерпно описують систему. Характерно, що власні значення матриці А співпадають з полюсами передатної функції.

Сьогодні опис (3.12) отримав надзвичайне широке розповсюдження: він дуже зручний для виконання розрахунків на ЕОМ, застосовний для багатовимірних систем, а також дозволяє виявити їх нові якості, таки як управляємість, спостережуваність та інші.