Министерство образования и науки РФ
Государственное образовательное учреждение высшего профессионального образования
«Санкт-Петербургский государственный инженерно-экономический университет»
Лабораторная работа №2
«Статистический анализ парной связи»
Выполнила студентка гр. 1003
Свитина Дарья
Санкт-Петербург
2012
Содержание:
Исходные данные
1. Теоретическое обоснование связи между признаками с выделением признака-результата и признака-фактора.
2. Аналитическая равнонаполненная группировка.
3. Комбинационная группировка.
4. Построение графиков: корреляционного поля и эмпирической линии регрессии.
5. Проведение дисперсионного анализа по данным аналитической группировки.
6. Расчет показателей тесноты связи:
- эмпирического коэффициента детерминации и эмпирического корреляционного отношения;
- линейного парного коэффициента корреляции.
7. Построение линейной парной регрессии
8. Построение нелинейной регрессии – параболы
9. Построение нелинейной регрессии – равносторонней гиперболы.
10. Выбор лучшего уравнение регрессии.
Исходные данные:
Сведения об обслуживании клиентов
№ Клиента |
Удовлетворенность обслуживанием Y |
Количество посещений X |
1 |
5 |
3 |
2 |
1 |
1 |
3 |
3 |
1 |
4 |
3 |
2 |
5 |
6 |
5 |
6 |
9 |
7 |
7 |
2 |
2 |
8 |
4 |
3 |
9 |
3 |
1 |
10 |
7 |
4 |
11 |
5 |
2 |
12 |
4 |
3 |
13 |
5 |
1 |
14 |
4 |
2 |
15 |
3 |
2 |
16 |
7 |
4 |
17 |
7 |
5 |
18 |
5 |
3 |
19 |
1 |
1 |
20 |
4 |
3 |
Теоретическое обоснование связи между признаками с выделением признака-результата и признака-фактора
Так как конкретному набору значений результата соответствует некоторое множество (распределение) величин результата и рост фактора меняет распределение результата, то это говорит о наличии статистической связи.
Аналитическая равнонаполненная группировка
Отчет |
|||
Удовлетворенность обслуживанием |
|||
№ группы |
Средний балл удовлетворенности |
N |
Стд.Отклонение |
1,00 |
2,6000 |
5 |
1,67332 |
2,00 |
3,4000 |
5 |
1,14018 |
3,00 |
4,4000 |
5 |
,54772 |
4,00 |
7,2000 |
5 |
1,09545 |
Итого |
4,4000 |
20 |
2,08756 |
Вывод: так как с увеличением количества посещений удовлетворенность обслуживанием растет, то между количеством посещений и удовлетворенностью обслуживанием прямая(возрастающая) зависимость.
Комбинационная группировка
|
Группы по удовлетворенности обслуживанием |
Итого |
||||
1,00 |
2,00 |
3,00 |
||||
Группы по количеству посещений |
1,00 |
4 |
1 |
0 |
5 |
|
2,00 |
3 |
2 |
0 |
5 |
||
3,00 |
0 |
5 |
0 |
5 |
||
4,00 |
0 |
0 |
5 |
5 |
||
Итого |
7 |
8 |
5 |
20 |
||
Вывод: Зависимость между количеством посещений и удовлетворенностью обслуживанием прямая, т.к. значения располагаются ближе к главной диагонали
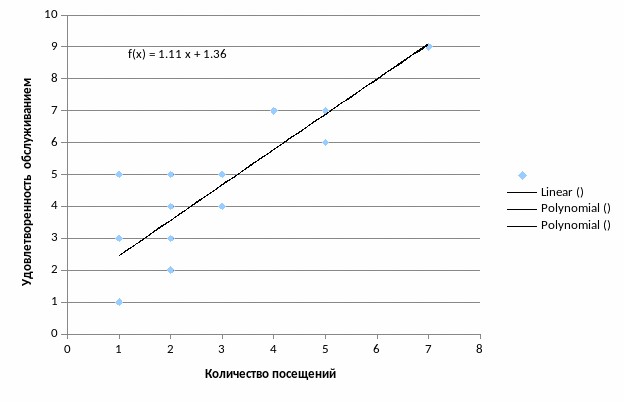
Построение графиков: корреляционного поля и эмпирической линии регрессии
Нижн. гр. |
Верх. гр |
Число ед. |
Сумма |
Среднее |
Дисперсия |
1 |
2 |
5 |
13 |
2,6 |
2,8 |
2 |
3 |
5 |
17 |
3,4 |
1,3 |
3 |
5 |
5 |
22 |
4,4 |
0,3 |
5 |
7 |
5 |
36 |
7,2 |
1,2 |
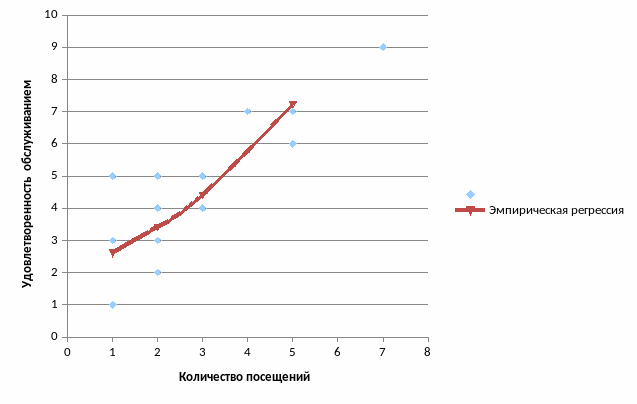
Вывод: с увеличением количества посещений удовлетворенность обслуживанием растет
Проведение дисперсионного анализа по данным аналитической группировки
Дисперсионный анализ |
|
|
|
|
|
|
Источник вариации |
SS |
df |
MS |
F |
P-Значение |
F критическое |
Между группами |
60,4 |
3 |
20,13333 |
14,38095 |
8,35E-05 |
3,238872 |
Внутри групп |
22,4 |
16 |
1,4 |
|
|
|
|
|
|
|
|
|
|
Итого |
82,8 |
19 |
|
|
|
|
Вывод: так как Fнабл>Fкрит, то связь статистически значимая.
Расчет показателей тесноты связи
- эмпирического коэффициента детерминации и эмпирического корреляционного отношения
Эмпирический коэффициент детерминации |
Эмпирическое корреляционное отношение |
0,729469 |
0,854089 |
Вывод: так как величина эмпирического корреляционного отношения равна 0,854089, то связь между количеством посещений и удовлетворенностью обслуживанием тесная.
- линейного парного коэффициента корреляции
Линейный парный коэффициент корреляции |
0,856941 |
Вывод: так как величина линейного парного коэффициента корреляции>0, то связь прямая.
Построение линейной парной регрессии
Регрессионная статистика |
|
Множественный R |
0,856941112 |
R-квадрат |
0,734348069 |
Нормированный R-квадрат |
0,719589628 |
Стандартная ошибка |
1,105440583 |
Наблюдения |
20 |
Дисперсионный анализ |
|
|
|
|
|
|
df |
SS |
MS |
F |
Значимость F |
Регрессия |
1 |
60,8040201 |
60,8040201 |
49,75784 |
1,40146E-06 |
Остаток |
18 |
21,9959799 |
1,221998883 |
|
|
Итого |
19 |
82,8 |
|
|
|
|
Коэффициенты |
Стандартная ошибка |
t-статистика |
P-Значение |
Нижние 95% |
Верхние 95% |
Нижние 95,0% |
Верхние 95,0% |
Y-пересечение |
1,359798995 |
0,496846109 |
2,736861517 |
0,013547 |
0,315964056 |
2,403634 |
0,315964 |
2,403634 |
Переменная X 1 |
1,105527638 |
0,156725211 |
7,053923451 |
1,4E-06 |
0,77626019 |
1,434795 |
0,77626 |
1,434795 |
Уравнение парной регрессии f(x)=1,35978995+1,105527638*x