Санкт-Петербургский

Государственный Электротехнический Университет

Лабораторная работа №3

«Исследование свободных процессов в электрических цепях»

Выполнили: Зуев И. Проверил: Гончаров В.Д.

Группа: 9132

Факультет: РТ

Санкт-Петербург

2001

Цель работы: изучение связи между видом свободного процесса в электрической цепи и расположением собственных частот (корней характеристического уравнения) на комплексной плоскости; приближенная оценка собственных частот и добротности RLC – контура по осциллограммам.

П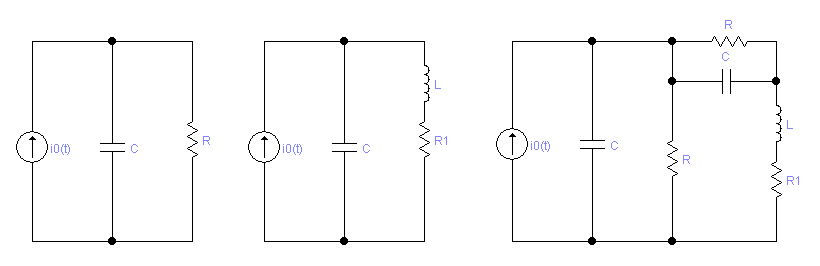 одготовка к работе. В работе предлагается исследовать процессы в цепях, схемы которых представлены ниже на рисунке. Цепи возбуждаются очень короткими импульсами тока i₀(t), заряжающими емкость С. В паузах между импульсами емкость разряжается, цепь находится в свободном режиме, так как в это время источник возбуждения отключен (i₀=0).

В линейных цепях свободный процесс описывается линейными дифференциальными уравнениями и его вид определяется корнями характеристического уравнения (собственными частотами цепи p_k).

При возбуждении цепи источником тока собственные частоты можно рассчитать как нули входной проводимости Y(p):

а) для цепи первого порядка (первый рисунок),, откуда (1)

б) для цепи второго порядка (второй рисунок), , откуда

(2)

в) для цепи третьего порядка, третий рисунок:

, откуда

, (3)

Общий вид решения для напряжения любого элемента цепи

где А_к – постоянные интегрирования, n – порядок цепи.

У цепи первого порядка одна собственная частота (1), вещественная и отрицательная, свободный процесс имеет вид

; (4)

процесс экспоненциальный, причем  - постоянная затухания, а  - постоянная времени экспоненты. Временная диаграмма свободного процесса показана на рисунке ниже, а, причем  - интервал времени, соответствующий любой подкасательной к экспоненте.

В цепи второго порядка две собственные частоты (2) могут быть вещественными (апериодический режим, рисунок б) или комплексно-сопряженными. Комплексно-сопряженным частотам соответствует качественно новый характер свободного процесса – колебательный:

(5)

где  - постоянная затухания,  - частота затухающих колебаний (). Временная диаграмма колебательного процесса представлена на рисунке ниже в.

В цепи второго порядка возможен также критический режим (, кратные собственные частоты); вид процесса близок к диаграмме, показанной на рисунке б, причем момент достижения максимума , если .

Д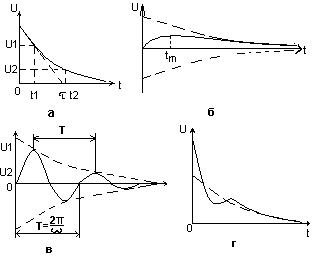 альнейшее увеличение порядка цепи к качественно новым явлениям не приводит. Так, согласно (3), в схеме изображенной на 3 рисунке выше, собственные частоты могут быть либо все три вещественные, либо одна – вещественная и две – комплексно-сопряженные. Временная диаграмма свободного процесса представлена на рисунке ниже, г –это сумма экспоненты и затухающей синусоиды.

В некоторых случаях собственные частоты относительно просто рассчитываются по осциллограммам. Например, согласно (4) по рисунку а, можно рассчитать постоянную затухания

Для случая рисунка в, постоянная затухания  также может быть определена на основании (6), но при этом обязательно выполнено условие , что вытекает из (5).

В случае рисунка б и г, найти собственные частоты можно лишь приближенно, выделив, как показано пунктиром, отдельные составляющие процесса.

Особый интерес представляет определение добротности Q RLC – контуров по виду свободного процесса. Для последовательного RLC – контура

где - частота незатухающих колебаний в идеальном контуре (R₁=0). Согласно (2) собственные частоты последовательного RLC – контура можно записать следующим образом:

причем Q<0,5 соответствует апериодический режим, Q=0,5 – критический режим, Q>0,5 - колебательный режим, а Q= - незатухающий колебательный режим.

При Q>10 с высокой степенью точности можно считать

С учетом (6) формула, позволяющая в этом случае определить добротность по осциллограмме рисунка в, имеет вид

Для повышения точности можно брать отношение напряжений за n периодов колебаний:

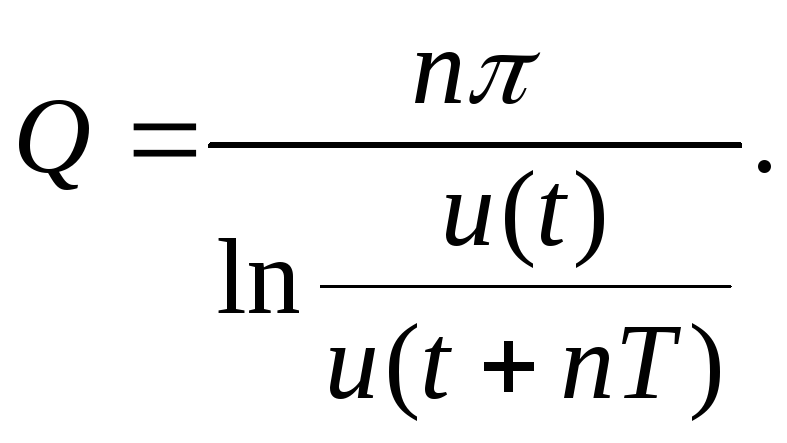
Исследование свободных процессов в цепи первого порядка.

1. Осциллографируемый процесс описывается аналитической формулой: .

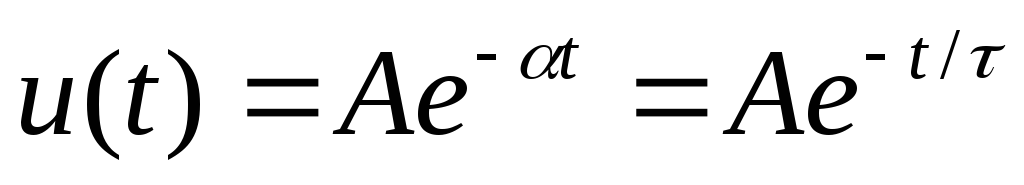2. Собственная частота определяется по осциллограмме, определяется по формуле 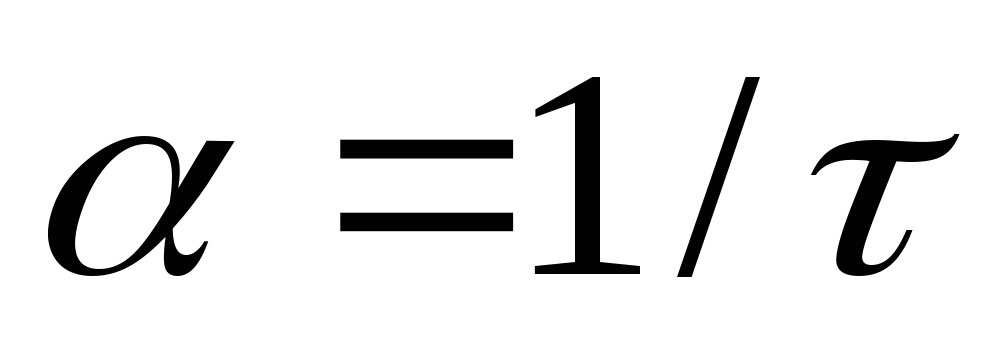, где =1 мс, тогда =10 000. Что соответствует теоретическому расчету .

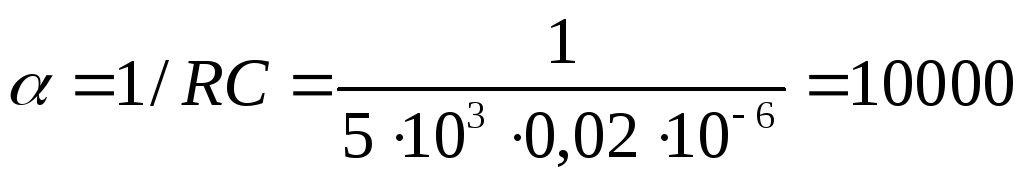Исследование свободного процесса в цепи второго порядка

3. Графики процессов описываются следующим выражением .

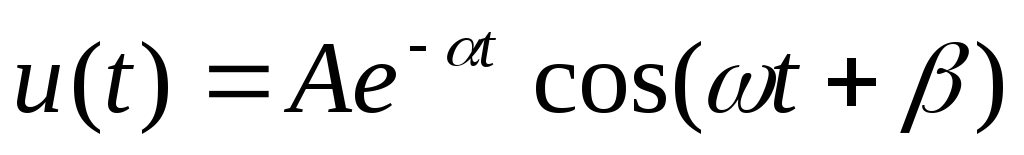4. Для того, чтобы определить по осциллограмме собственную частоту цепи нужно найти период импульса , где Т_с= 1 мс – длительность сигнала, 3/10 – доля периода в этом сигнале. Тогда воспользуемся формулой 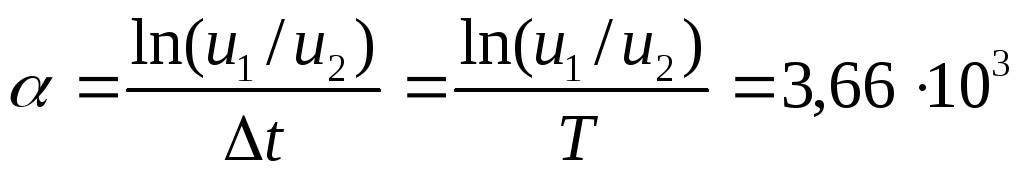. . 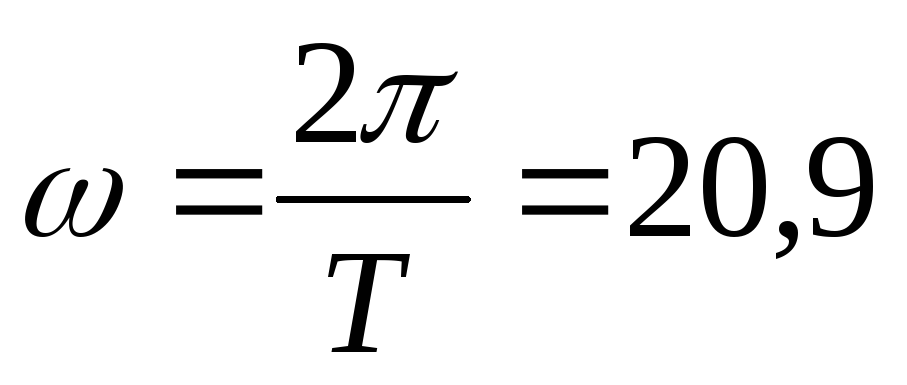Результат выглядит следующим образом:

, отличается от теоретического расчета:

.

Возможно здесь ошибка из-за неточности измерения или неверности зарисовки диаграммы.

5. Найдем теоретические значения формуле (2):

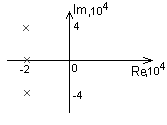
Этим данные соответствуют осциллограммы, т.к. известно. Что при одинаковых корнях график имеет вид выше рисунка б.

6. Рассчитаем добротность контура по формуле 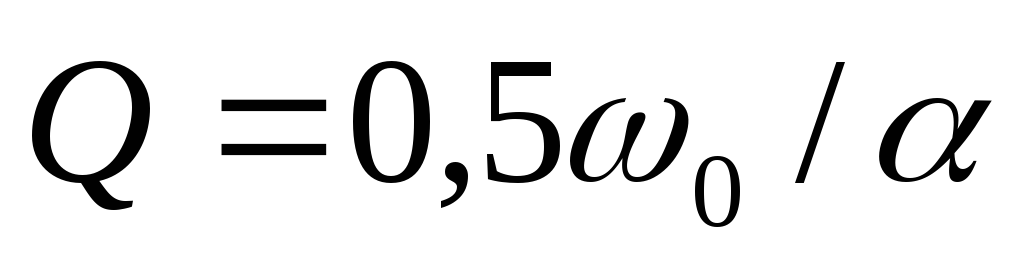, тогда для R₁=0,5 кОм: Q=2,236. Для воспользуемся последней формулой: R₁=0: Q=6,14

Исследование свободных процессов в цепи третьего вопроса

7. Аналитическое выражение .

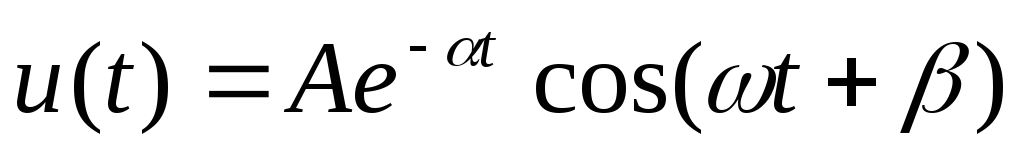8. Значение собственных частот цепи согласно формуле (3):

Что соответствует полученным осциллограммам, т.к. идет сложение 3 колебаний и рисунок похож на рисунок в, что еще раз подтверждает верность проделанного эксперимента.

Заключение: В результате выполненной работы было изучены свободные процессы в электрических цепях, результаты показали, что все опыты верны, с небольшой погрешностью.