
Лабораторная работа №31
.DOCЦель работы: изучение связи между видом свободного процесса в электрической цепи и расположением собственных частот (корней характеристического уравнения) на комплексной плоскости; приближенная оценка собственных частот и добротности RLC–контура по осциллограммам.
Экспериментальные исследования.
Установить на выходе генератора синусоидальных импульсов напряжение U = 7 – 10 В, частоту fc = 2 кГц, подключить его на вход цепи.










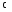

Собрать схему, показанную на рисунке, (C=0,02 мкФ, R=5 кОм). Снять осциллограмму напряжения на конденсаторе, зафиксировав на ней полный период сигналов Tc = 1/fc = 0,5 мс (он определяет масштаб по оси времени).
Данный процесс описывается затухающей экспонентой с постоянным коэффициентом. Так как процесс свободный, то вынужденной составляющей нет.
По
осциллограмме можно определить t
как x-координату
точки пересечения касательной к
осциллограмме в начальной точке с осью
абсцисс. Это можно проверить по формуле
![]() .
Собственная частота — p1
=
–10
4
c–1.
.
Собственная частота — p1
=
–10
4
c–1.
Цепь второго порядка.



















Изменяя R1, рассмотреть критический режим (граничный между колебательным и апериодическим). Снять его осциллограмму и записать R1кр.

Общий
вид выражения для исследованных
процессов:
![]() ,
где a
или b
могут быть и комплексными (колебательный
случай).
,
где a
или b
могут быть и комплексными (колебательный
случай).
Собственные частоты цепи, которая соответствует первой осциллограмме, можно определить, исходя из формул
![]() a
также можно найти на основе осциллограммы,
как отношение логарифма отношения
значений напряжений двух соседних
максимумов и временной разности (периода)
между этими двумя максимумами (a
= 1/t
= ln(u1
/
u2)
/ Dt).
Ó íàñ a
= ln 10 / (2,2×10–4)
= 10466 »
10000!
a
также можно найти на основе осциллограммы,
как отношение логарифма отношения
значений напряжений двух соседних
максимумов и временной разности (периода)
между этими двумя максимумами (a
= 1/t
= ln(u1
/
u2)
/ Dt).
Ó íàñ a
= ln 10 / (2,2×10–4)
= 10466 »
10000!


Добротность
контура вычисляется по формуле
![]() .
Мы вычисляем Q(R1).
Q(500)=2,236.
Q(0)
= ¥.
Так как контур у нас не идеальный, то
такого не может быть и лучше воспользоваться
формулой
.
Мы вычисляем Q(R1).
Q(500)=2,236.
Q(0)
= ¥.
Так как контур у нас не идеальный, то
такого не может быть и лучше воспользоваться
формулой
![]() .
.
Цепь третьего порядка.







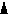


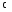


















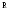
Полученный график описывается суммой экспоненты и затухающей синусоиды.


