
- •1. Определение алгоритма и способы их записей.
- •2. Принятые обозначения при описании алгоритмов.
- •3. Пошаговое описание алгоритмов.
- •4. Описание алгоритмов в виде блок-схем.
- •5. Свойства алгоритмов.
- •6. Критерии эффективности и сложность алгоритмов.
- •7. Классификация задач по степени сложности.
- •8. Сущность метода математической индукции (ми).
- •9. Построение доказательства по методу ми.
- •10. Примеры доказательств с использованием метода ми.
- •11. Использование метода ми для исследования алгоритмов (на примере обобщенного алгоритма Евклида).
- •12. Недетерминированные и детерминированные алгоритмы.
- •13. Разделы математической логики, представление операций булевой логики через множества и их отображение с помощью диаграмм Эйлера-Венна.
- •14. Объединение множеств и переход от предметной переменной х к логическим переменным х1 и х2 .
- •15. Пересечение множеств, тавтология, противоречие, дополнение и области взаимодействия двух множеств на диаграмме Эйлера-Венна.
- •16. Таблицы истинности для дизъюнкции и конъюнкции.
- •17. Операции стрелка Пирса и штрих Шеффера.
- •18. Операции разности и импликации.
- •19. Операции симметрической разности и эквивалентности.
- •20. Формы представления булевых функций (сднф, скнф, спнф).
- •21. Двойственность в булевой логике.
- •22. Различия отображения логических функций в сднф. Скнф и спнф. Переход из сднф в спнф.
- •23. Минимальные нормальные формы логических функций.
- •24. Принцип суперпозиции в булевой логике и приоритеты логических операций.
- •25. Классы элементарных логических функций.
- •26. Законы логики Буля.
- •27. Применение закона поглощения для нескольких переменных.
- •28. Аксиоматический подход к доказательству логических выражений в булевой
- •29. Доказательство логических выражений с помощью диаграмм Эйлера-Венна.
- •30. Доказательство логических выражений с использованием таблиц истинности.
- •31. Способы доказательства логических выражений с использованием специальных приемов.
- •32. Логика высказываний и операции логики высказываний.
- •33. Таблицы истинности операций логики высказываний.
- •34. Различия логики Буля и логики высказываний.
- •35. Метаязык логики высказываний и переход от импликативной формы к высказываниям на метаязыке.
- •36. Аксиомы, противоречия и тавтологии в логике высказываний.
- •37. Конструктивный подход к доказательству логических выражений в логике высказываний.
- •38. Минимальная нормальная форма, минимальное и трансверсальные покрытия в логике высказываний.
- •39. Доказательство логических высказываний с помощью метода резолюций.
- •40. Логика предикатов.
- •41. Минимизация логических выражений методом Куайна (Квайна).
- •42. Минимизация логических выражений в логике Буля путем склеивания в сднф и скнф. Показать, в чем различие склеивания в этих двух формах.
- •43. Асимптотические представления и анализ алгоритмов.
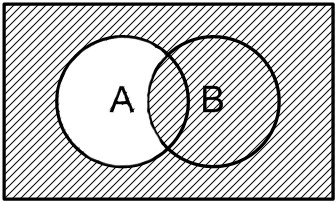
18. Операции разности и импликации.
Разностью множеств A и B, это множество, которое вошло в A, но не вошло в B:
А – В = {1,2,4,6} – {3,4,8,9,2} = {1,6} = C1
Дополнение к разности называется импликацией
-
 импликация
импликация
A \ B (A - B) A → B
Таблицы истинности:
Разность |
|
Импликация |
||||
X1 |
X2 |
Y = X1 - X2 |
|
X1 |
X2 |
Y = X1→X2 |
0 |
0 |
0 |
|
0 |
0 |
1 |
1 |
0 |
1 |
|
1 |
0 |
0 |
0 |
1 |
0 |
|
0 |
1 |
1 |
1 |
1 |
0 |
|
1 |
1 |
1 |
Для данных операций можно записать:
![]()
![]()
19. Операции симметрической разности и эквивалентности.
Симметрическая разность двух множеств А и В – это объединение следующих двух разностей, то есть
А + В = (А - В) v (B - A) = {1,6} v {3,8,9}= {1,3,6,8,9} = C1 v C2
Д ополнительной к данной операции является операция эквивалентности, которая определяется теми же элементами множества А и В, которые являются для них общими, при этом элементы не входящие ни в А ни в В также являются эквивалентными.
![]()
Симметричная разность Эквивалентность

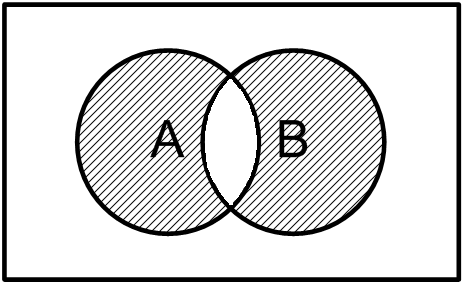
A + B A ~ B
Разность |
|
Импликация |
||||
X1 |
X2 |
Y = X1 + X2 |
|
X1 |
X2 |
Y = X1 ~ X2 |
0 |
0 |
0 |
|
0 |
0 |
1 |
1 |
0 |
1 |
|
1 |
0 |
0 |
0 |
1 |
1 |
|
0 |
1 |
0 |
1 |
1 |
0 |
|
1 |
1 |
1 |
Симметричную разность имеет другие названия: строгая дизъюнкция, исключительная альтернатива, сложение по модулю.
Из определения операции симметричной разности и эквивалентности следует:
![]()
![]()
20. Формы представления булевых функций (сднф, скнф, спнф).
Любую
булеву функцию y=f(a,b)
можно представить как комбинацию
областей:

Тогда
в зависимости от значения функций и
заданных
![]() ,
которые именуются констинтуентами,
получим 16-ть конечных операций, которые
в общем виде можно записать:
,
которые именуются констинтуентами,
получим 16-ть конечных операций, которые
в общем виде можно записать:
![]()
Такая форма представления называется СДНФ (совершенно-дизъюнктивная нормальная форма)
В ней констинтуенты – коньюнты соединяются с помощью дизъюнкции.
В логике Буля действует принцип двойственности, который говорит, если одновременно заменить все конъюнкции на дизъюнкции, или наоборот (все ^ на v), замене символов (конъюнкция на дизъюнкцию и 0 на 1), то все логические равенства остаются в силе.
![]()
Такая форма представления логических функций называется СКНФ (совершенная коньюктивная нормальная форма). В ней констинтуенты – дизъюнкты, соединяются с помощью конъюнкции.
Существует также третья форма представления логических функций СПНФ – совершенная полиномиальная нормальная форма. Ее можно получить из СДНФ путем следующей замены:
![]()
Так как СДНФ все констинтуенты не пересекаются, то можно записать:

