15. Пересечение множеств, тавтология, противоречие, дополнение и области взаимодействия двух множеств на диаграмме Эйлера-Венна.
Пересечение Ма ∩ Мb двух множеств Ма и Мb является множество М, состоящее из элементов, которые принадлежат как множеству Ма так и множеству Мb:
М= Ма ∩ Мb = {mi/miЄ Ма и miЄ Мb} союз ‘и’ можно заменить знаком &
Д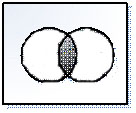
ля
операций алгебры Кантора выполняются
следующие законы:
Коммутативность объединения
Ма ∩ Мb= Мb ∩ Ма
Ассоциативность объединения
Ма ∩ ( Мb ∩ Мс)=( Ма ∩ Мb) ∩ Мс
Дистрибутивность пересечения относительно объединения и объединение относительно пересеченияМа ∩ (Мb U Мс) = (Ма ∩ Мb) U (Ма ∩ Мс)
Ма U Мb Ма U (Мb ∩ Мс) = (Ма U Мb) ∩ (Ма U Мс)
Ма U (Мb ∩ Мс) = (Ма U Мb) ∩ (Ма U Мс)
И демпотентность объединения
Ма ∩ Ма = Ма
Действия с универсальными 1 и пустыми Ø множествами
М ∩ Ø = Ø, М ∩ 1 = М, М ∩ = Ø
Де-Моргана
двойного
дополнения
Тавтология
– логическое выражение, которое всегда
является истинным, вне зависимости от
значения х.Противоречие
–
всегда ложное логическое выражение,
вне зависимости от х.
дополняет А до фундаментального множества
V,
поэтому операция, которая позволяет
получить не А,
называется дополнением.Дополнением
к логическим переменным
- отрицание
х
16. Таблицы истинности для дизъюнкции и конъюнкции.
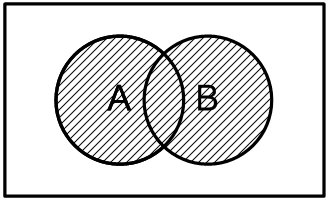
Между таблицами истинности и диаграмм Эйляра-Венна существует взаимно-однозначное соответствие: количество единиц совпадает с количеством заштрихованных областей. Нетрудно посчитать что число всех возможных комбинаций 0 и 1 равно 16 (от 0000 до 1111) это означает что общее количество логических операций равно этому числу.
Общее количество логических операций для двух переменных 24 = 16. Для любой логической операции существует двойственная к ней.
Дизъюнкция |
|
Конъюнкция |
||||
X1 |
X2 |
Y = X1 v X2 |
|
X1 |
X2 |
Y = X1 ^ X2 |
0 |
0 |
0 |
|
0 |
0 |
0 |
1 |
0 |
1 |
|
1 |
0 |
0 |
0 |
1 |
1 |
|
0 |
1 |
0 |
1 |
1 |
1 |
|
1 |
1 |
1 |
17. Операции стрелка Пирса и штрих Шеффера.
Эти операции дополняют объединение и пересечение до фундаментального множества соответственно.
На языке логических формул это записывается следующим образом:
С
трелка
Пирса
– это дополнение к объединению
Штрих Шеффера – дополнение к пересечению
Таблицы истинности
Стрелка Пирса |
|
Штрих Шеффера |
||||
X1 |
X2 |
Y = X1 ↓ X2 |
|
X1 |
X2 |
Y = X1 | X2 |
0 |
0 |
1 |
|
0 |
0 |
1 |
1 |
0 |
0 |
|
1 |
0 |
1 |
0 |
1 |
0 |
|
0 |
1 |
1 |
1 |
1 |
0 |
|
1 |
1 |
0 |
Из диаграмм Эйлера-Венна и таблице истинности видно:
Стрелки
Пирса:
Штрих
Шеффера:
