2. Аксиомы статики

АКСИОМА 1. Первый закон механики, закон инерции, или закон Галилео Галилея. Закон читается так;

В сякое тело находится в состоянии покоя или равномерного и прямолинейного движении, если на него не действуют никакие силы.

Эта аксиома применима к объектам, которые движутся по отношению к неподвижной системе или по отношению к неподвижному наблюдателю. На самом деле неподвижных систем нет: Земля, как планета, вращается вокруг своей оси и её нельзя считать неподвижной. Планета вращается вокруг своей оси, совершая полный оборот за сутки; ось вместе с Землей движется вокруг Солнца. Солнечная система со своими планетами движется во Вселенной. По этой аксиоме векторная сумма всех сил, действующая на тело, равна нулю в двух случаях: если рассматривать движение тела, то характер движения является равномерным, а траектория – прямой и если рассматривать состояние тела в покое. Например, движение поезда по прямолинейной траектории с постоянной скоростью. Это возможно при условии, что сила тяги и сила трения скольжения уравновешиваются между собой. Второе состояние поезда – это его покой.

АКСИОМА 2. Второй закон механики или основной закон механики.

Е сли на объект действует сила, то объект получает ускорение пропорциональное силе, вектор ускорения совпадает с направлением вектора силы.

Это основной закон механики, вы его знаете со школы, изучая курс физики в разделе «Механика».

В статике мы будем рассматривать состояние объекта в покое, следовательно, скорость и ускорение его равны нулю. Отсюда сделать можно вывод: любые объекты находятся под действием сил, поскольку мы рассматриваем состояние покой, то векторная сумма сил, действующая на объект, равна нулю. Но в динамике второй закон механики лежит в основе составления дифференциальных уравнений движения объекта.

Надо сказать, что этот закон применим только к объектам, имеющим большие размеры и которые движутся с небольшими скоростями. Например, движение тел со скоростью света мы не рассматриваем. Движение маленьких тел, например, чаинок в стакане при равномерном вращении его не подчиняются этому закону: согласно закону механики они должны убегать от центра под действием центробежной силы, а они движутся к центру.

АКСИОМА 3. Третий закон механики или закон действия и противодействия.

В сякому действию есть равное по величине и противоположно по направлению противодействие.

Как этот закон можно применить к телу? Согласно этому закону расстояние между любыми точками тела является постоянным, это может быть тогда, когда мы рассматриваем абсолютно твердое тело. Допустим, рассмотрим действие силы с одной точки тела на другую и наоборот. Увидим две внутренние силы, которые являются уравновешенными и эквивалентными нулю. Значит, при действии всех внутренних сил точек тела друг на друга имеем: главный вектор всех внутренних сил равный нулю:

или

Рис. 13

Если рассматриваем систему твердых тел, связанных между собой определенными связями, т.е. механическую систему, то в этом случае она должна быть неизменяемой по этой же аксиоме.

Например, рассмотрим ременную передачу. Она состоит из шкивов и ремня. Шкивами являются твердые тела, а ремень - гибкая связь, причем, идеальная, у которой расстояние постоянное между любыми её точками.

АКСИОМА 4. Аксиома параллелограмма.

Аксиома параллелограмма позволяет две сходящиеся силы приводить к равнодействующей (см. рис.14, а).

Д ве силы, линии действия которых пересекаются, приводятся к равнодействующей.

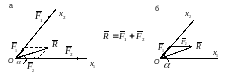
Рис. 14

Модуль равнодействующей силы равен:

.

К такой равнодействующей силе приводятся сходящиеся силы, сложенные по правилу треугольника (см. рис.14, б).

Правило удобно применять при сложении нескольких сил, получается силовой многоугольник, как это было видно при сложении четырех сходящихся сил (см. п.1,2, с.8).

Правило параллелограмма позволяет раскладывать силу на её проекции в координатных и естественных осях и выполнять обратное действие–сложение проекций.

АКСИОМА 5. Аксиома присоединения.

И ли аксиома присоединения уравновешенной системы сил. Действие системы уравновешенных сил не изменяет состояние тела.

Допустим, объект под действием заданных сил находится в определенном состоянии. После этого приложили к этому объекту другую систему сил, эквивалентную нулю. Говоря языком первоклассника: если к числу прибавить ноль или отнять его, то от этого результат не изменится. Значит: состояние объекта не нарушится, если на него действует уравновешенная система сил (см. рис.15).

Рис. 15

А КСИОМА 6. Аксиома освобождаемости от связей. Всякое несвободное тело можно рассматривать как свободное, если убрать связи и заменить их реакциями связей.

В природе нет свободных тел, они все каким-то образом ограничены в движении и связаны с другими объектами. Это зависит от вида крепления тела к другому. Если есть ограничение в движении, то существует связь. А если есть связь, то есть реакции связей, т.е. реактивные силы, они зависят от вида опоры. Всего таких опор двенадцать. Мы их рассмотрим после аксиомы 7 (см.п.3).

А КСИОМА 7. Аксиома отвердевания.

Свойство тела не изменится при его отвердевании.

Эта аксиома позволяет рассматривать все объекты абсолютно твердыми, следовательно, любая реальная задача решается приближенно, потому что реальные тела имеют свойство деформироваться.

Контрольные вопросы

1. Сколько аксиом Вы знаете?

2. Объясните суть первой аксиомы.

3. Объясните суть второй аксиомы.

4. Объясните суть третьей аксиомы.

5. О чем говорится в аксиоме параллелограмма?

6. О чем говорит аксиома присоединения уравновешенной системы сил?

7. Объясните аксиому отвердевания?

8. Изменится ли состояние тела от переноса силы вдоль её линии действия?