По месту действия силы
Сосредоточенная сила.
С ила, действующая на тело в какой-нибудь точке, называется сосредоточенной силой.
Например, удар молота о наковальню. На рис.7 показана действующая сила в точке А данного тела-бруса, является сосредоточенной силой.
Рис. 7
Кроме сил, действующих в одной точке, есть силы, которые действуют на определенную длину и на конкретную площадь объекта. Такие силы называют распределенными. Рассмотрим их действие на конкретной длине объекта.
Распределенные силы.
С
илы
параллельные и ориентированные в одну
сторону с интенсивностью q
с размерностью
, называются распределенными.
Они
заменяется сосредоточенной силой
,
которая равна площади фигуры и находится
в её центре (см. рисунки 8, 9, 10 ).
В качестве примера возьмем любой строительный материал: доски, кирпичи, цемент и т.д., которые лежат на полу, они могут быть расположены произвольно и давить на пол с интенсивностью q .
Р
ассмотрим
приведение распределенной нагрузке по
линейному и нелинейному законам. На
рис.8а на балку по длине l
действует
распределенная сила с интенсивностью
q
, её размерность равна [H/м].
В поперечном сечении показан прямоугольник,
это значит, что интенсивность q
постоянна по всей длине l.
Центр
прямоугольника как фигуры находится
на пересечении диагоналей, в которой
находится сосредоточенная сила,
эквивалентная распределенной нагрузке
и она равна площади этой фигуры (см.
формулу (1)).
а б
в г
Рис. 8
(1)
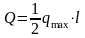(3)
На рис.8б
тоже показана распределенная нагрузка,
которая изменяется по линейному закону.
На рис рис.8в тоже однородный, но
прямоугольный треугольник, найдем центр
тяжести этого треугольника. Для этого
рассмотрим рис.8г, где показан однородный
треугольник, мысленно отрежем тонкую
полоску со стороны АВ, центр тяжести её
находится в середине, если после первой
полоски также отрезать вторую полоску,
то получаем центр тяжести в середине,
значит середина каждой полоски, которая
параллельна стороне находится на медиане
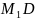стороны АВ. Рассуждая также для стороны
AD
данного треугольника ABD,
получим, что центр тяжести однородного
треугольника находится на пересечении
медиан
и
.
Положение центра тяжести или точки С,
показана на рис. 8в и расположена на 1/3
высоты от основания. Положение центра
тяжести для распределенной нагрузки,
которая изменяется по линейному закону
для рис.8б и рис.8в, найдено аналогично
и находится на пересечении медиан.
Величина сосредоточенной силы находится
по формуле (2) см. рис.8б и по формуле (3)
см. рис.8в.
Задание.
Самостоятельно найдите положение центра тяжести и величину силы на рис. 9а, рис. 9б.
а
б
Рис. 9
По известности
1. Активная сила. Под активной силой подразумевается известная по величине и направлению сила, которая действует на объект. Например, сила тяжести, сила ветра, сила удара и т.д.
2. Реактивная сила. Реактивная сила неизвестная по величине и направлению, зависит от крепления одного объекта к другому и от действия активных сил. Рассматривается реактивная сила после прохождения различных опор и аксиомы 6 . Реактивная статическая сила находятся из расчета на равновесие объекта. Направление реактивной силы зависит от вида опоры, которая ограничивает движение тела в месте её крепления.