6. Приведение силы к новому центру или теорема Пуансо

Эта теорема нужна при приведении произвольно расположенных сил к точке или к заданному центру. Для разберем правило приведения одной силы к заданному центру.

Теорема Пуансо.

С остояние тела не изменится, если силу параллельно перенести в новый центр и добавить момент этой силы относительно нового центра.

Докажем теорему см. рис. 50.

Дано: Тело. В точке А действует сила .

Доказать или ответить на вопрос: Как, не изменяя состояние тела, перенести силу в любую точку тела, например, в точку В?

1. Для доказательства этой теоремы нам потребуются знания по теме «Пара сил и её свойство» и понятие «уравновешенные силы». Если Вы знаете, то приступаем к доказательству. В выбранной точке тела В приложим уравновешенную систему двух сил , но так, чтобы эти силы по модулю равны первоначальной силе

и , .

2. Теперь вместо одной силы имеем три силы . Две из которых представляют пару сил с моментом, который одновременно является момент заданной силы относительно нового центра . На рис. 50 последовательно показан переход от одной силы к трем и окончательному приведению.

3. Поскольку пара сил представляет собой момент, вектор его является вектором свободным, то первоначальная точка А остается свободной, а в новой точке В приложена первоначальная сила, которая параллельна перенесена и момент пары сил равный моменту первоначальной силы относительно новой точки см. рис. 50. Теорема доказана.

Рис. 50

Задание.

1. Дан ломаный уголок, который изогнут под прямым углом. Длинная сторона уголка в горизонтальном положении крепится к вертикальной стене короткой стороной уголка с помощью болта. На свободный конец уголка действует вертикальная сила, направленная вниз.

Привести эту силу к точке крепления уголка со стеной.

2. Дан ломаный уголок, который изогнут под прямым углом. Длинная сторона уголка в вертикальном положении крепится к горизонтальной плоскости короткой стороной уголка с помощью болта. На свободный конец уголка действует горизонтальная сила, направленная влево.

Привести эту силу к точке крепления уголка с плоскостью.

7. Приведение системы сил к центру

Используя правило приведения силы к заданному центру, сложим три произвольно расположенные силы в пространстве см. рис. 51а.

Дано: Первая сила действует в плоскости Oxz, плоскости 1 из точки А. Вторая сила действует в плоскости Oxy, плоскости 2 из точки В. Третья сила действует в плоскости Oyz, плоскости 3 из точки С.

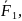
Задание. Привести заданные силы к точке О.

Решение. Приводим силу к заданному центру. В начале параллельно перенесем ее в новый центр. Для определения вектора момента первой силы относительно точки О проведем плоскость через радиус-вектор и вектор силы , получим заштрихованную плоскость, как показано на рис. 51а, рис. 51б. К этой плоскости из точки О нужно провести перпендикуляр, на котором находится вектор момента первой силы. Направление вектора момента находится по правилу буравчика – в нашей схеме вектор момента первой силы лежит на оси у в положительном направлении. Запишем: