
- •25. Процесс принятия решений: этапы, участники, основные задачи принятия решений.
- •26. Бинарные отношения. Операции над отношениями. Свойства бинарных отношений.
- •27. Бинарные отношения. Виды бинарных отношений. R-оптимальность.
- •28. Функции выбора. Логические формы функций выбора.
- •29. Функции выбора. Нормальные функции выбора.
- •30. Критериальное пространство. Бинарные отношения в критериальном пространстве.
- •31. Методы многокритериальной оптимизации. Метод линейной свертки
- •32. Методы многокритериальной оптимизации. Метод идеальной точки.
- •33. Методы многокритериальной оптимизации. Выбор с учетом числа доминирующих критериев.
- •34. Метод многокритериальной оптимизации. Метод анализа иерархий
- •35. Основная задача линейного программирования. Методы решений.
- •36. Двойственные задачи линейного программирования.
- •37. Транспортная задача.
- •38. Задача о назначении.
- •39. Динамическое программирование. Задача о замене оборудования.
- •40. Динамическое программирование. Мультипликативная задача.
- •41. Принятие решений в условиях полной неопределенности, в условиях риска
- •42. Принятие решений в условиях конфликта (Элементы теории игр). Основные понятия.
- •43. Задачи теории игр. Классификация игр.
- •44. Матричные игры. Решение матричной игры в чистых стратегиях. Смешанные стратегии.
- •45. Матричные игры. Сведение матричной игры к задаче линейного программирования.
- •46. Графоаналитические методы решения матричных игр.
- •47. Метод Брауна-Робинсон.
- •48. Методы экспертных оценок. Множества оценок экспертов.
- •49. Методы экспертных оценок. Типы шкал для измерения критериев.
- •Шкалы качественных признаков
- •Шкалы количественных признаков.
- •50. Методы обработки экспертной информации.
49. Методы экспертных оценок. Типы шкал для измерения критериев.
По экспертной информации о степени различия объектов устанавливается минимальный или близкий к минимальному набор критериев и оценок объектов по ним, обуславливающий указанные экспертами различия.
Основные типы шкал:
Шкалы качественных признаков
а) Номинальная шкала (шкала наименований) используется если нужно только различать объекты(не сравнивать)
При использовании номинальных шкал исследуемые объекты можно опознавать и различать на основе трех аксиом идентификации:
i либо есть j, либо есть не j;
если i есть j, то j есть i;
если i есть j и j есть k, то i есть k.
Факторы в данном случае выступают как ассоциативные показатели, обладающие информацией, которая может быть формализована в виде бинарных оценок двух уровней: 1 (идентичен) или 0 (различен).
б) Порядковая шкала – числа этой шкалы используются для различения объектов и установления порядка между ними.
В случаях, когда исследуемые объекты можно в результате сравнения расположить в определенной последовательности с учетом какого-либо существенного фактора (факторов), используются порядковые шкалы, позволяющие устанавливать равноценность или доминирование.
Предположим,
что необходимо расположить в определенной
последовательности n
объектов по какому-либо фактору
(критерию). Представим это упорядочение
в виде матрицы
 где i,
j
= 1,2,…, n.
где i,
j
= 1,2,…, n.
Величины устанавливают соотношения между объектами и могут быть определены следующим образом:
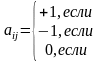
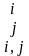

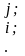
Установим
основные аксиомы, необходимые для
соблюдения условий упорядочения.
Соотношение
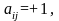 означающее, что i
предпочтительнее j,
должно быть ассиметричным, т.е., если
то
означающее, что i
предпочтительнее j,
должно быть ассиметричным, т.е., если
то
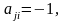 и транзитивным, т.е., если
и транзитивным, т.е., если
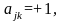 то
то
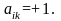
Соотношение
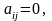 означающее, что i
и j
равноценны, называется соотношением
эквивалентности. Такое соотношение
должно быть
означающее, что i
и j
равноценны, называется соотношением
эквивалентности. Такое соотношение
должно быть
рефлексивным,
т.е.
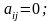
симметричным,
т.е., если
то
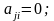
транзитивным,
т.е., если
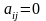 и
и
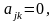 то
то
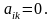
Кроме
того, эти два соотношения должны быть
совместимы, т.е., если
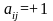 и
то
и
то
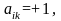 а также, если
и
то
а также, если
и
то
И,
наконец, упорядочение должно быть
связным, т.е. для любых i
и j
или
или
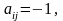 или
или
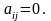
Использование порядковых шкал позволяет различать объекты и в тех случаях, когда фактор (критерий) не задан в явном виде, т.е. когда мы не знаем признака сравнения, но можем частично или полностью упорядочить объекты на основе системы предпочтений, которой обладает эксперт.
Шкалы количественных признаков.
а) Шкала интервалов. В ней нельзя отмерить естественно начало отсчета и естественную единицу измерения. Это задается экспертом.
Интервальные
шкалы предполагают возможность
трансформации оценок, полученных на
одной шкале, в оценки на другой шкале
при помощи уравнения
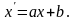
Разности между значениями на шкале интервалов становятся мерами на шкале отношений, т.е. на обычной числовой шкале, т.к. в результате вычитания можно избавиться от постоянного слагаемого b.
б) Шкала отношений. У нее существует естественное начало отсчета, но нет естественной единицы измрения.
Шкале отношений присуще свойство аддитивности. Наличие аддитивности выражается следующими аксиомами:
если j = a и i > 0, то i + j > a;
i + j = j + i;
если i = a и j = b, то i + j = a + b;
(i + j) + k = i + (j + k).
в) Шкала разности. У нее существует естественные единицы измерения, но нет естественного начала отсчета.
г) Абсолютная шкала. У нее единственные нуль и единица. Этим свойством обладает числовая ось. Другое важное свойство – безразмерность. Результатом разбиения являются обычные числа.
Шкала считается сильной, если в ней реализовано большее количество аксиом. При применении более сильной шкалы исследователь может получить неадекватную оценку. Использование более слабой шкалы влечет потерю информации.
