Тема: Функції багатьох змінних. Означення, границя та неперервність, похідні диференціали.

Як відомо, будь-який упорядкований набір з n дійсних чисел х₁…,х_n позначається (х₁,…,х_n) або М(х₁,…,х_n) і називається точкою n-вимірного арифметичного простору Rⁿ; числа х₁,…,х_n називаються координатами точки М(х₁,…,х_n). Відстань між точками М(х₁,…,х_n) і М^/(х^/₁,…,х^/_n) визначається за формулою

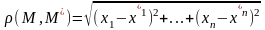
Нехай D 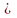Rⁿ – довільна множина n-вимірного арифметичного простору. Якщо кожній точці М(х₁,…,х_n) D поставлено у відповідність деяке цілком визначене дійсне число f(M)= f(х₁,…,х_n), то кажуть, що на множині D задана числова функція f : Rⁿ R від n змінних х₁…,х_n. Множина D називається областю визначення, а множина 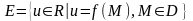- множиною значень функції f.

Зокрема, при n = 2 функцію двох змінних z = f(x,y),(x,y) D можна розглядати як функцію точок площини в тривимірному просторі з фіксованою системою координат О_xyz. Графіком цієї функції називається множина точок

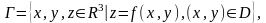
яка визначає, взагалі кажучи, деяку поверхню в R³.

Приклад 4. Знайти точки розриву функції

Функція не визначена в точках, в яких знаменник перетворюється в нуль. Тому вона має лінією розриву пряму 2х + 3у + 4 = 0.

Нехай (х⁰₁,…,х⁰_k,…x⁰_n) – довільна фіксована точка в області визначення функції u = f(х₁,…,х_n). Надаючи значенню змінної х_k приросту 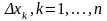, розглянемо границю

.

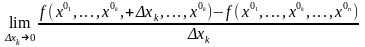Ця границя називається частинною похідною 1-го порядку функції по змінній x_k в точці (x⁰₁,…,x⁰_n) і позначається 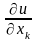або

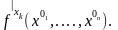
Обчислюються частинні похідні за звичайними правилами і формулами диференціювання, але при цьому всі змінні, крім x_k, розглядаються як сталі.

Частинними похідними 2-го порядку функції u=f(x₁,…,x_n) називаються частинні похідні від її частинних похідних першого порядку. Похідні другого порядку позначаються так:

Аналогічно визначаються і позначаються частинні похідні порядку вищого, ніж другий.

Результат багатократного диференціювання функції по різних змінних не залежать від черговості диференціювання за умови, що одержані при цьому змішані частинні похідні неперервні.

Повним приростом функці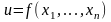ї в точці 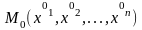, який відповідає приростам аргументів 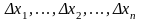, називається різниця

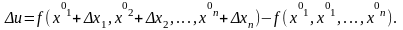
Функція u=f(M) називається диференційовною в точці М₀, якщо скрізь в околі цієї точки певний приріст функції можна подати у вигляді

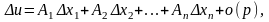
де 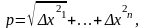A₁,…A_n – числа, не залежні від .

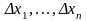Диференціалом 1-го порядку du функції називається вираз

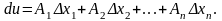
Диференціали незалежних змінних за означенням беруться рівними їх приростам: .

Для диференціала du правильна формула

Якщо p достатньо мале, то для диференційовної функції правильна наближена формула:

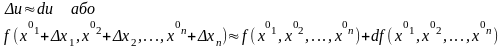
Диференціалом 2-го порядку d²u функції називається диференціалом від її диференціала 1-го порядку, розглянутого як функція змінних при фіксованих значеннях 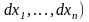: d²u = d(du). Аналогічно визначається диференціал 3-го порядку d³u = d(d²u). Взагалі, d^ku = d(d^k-1 u).

Диференціал k-го порядку функції , де х₁…х_n – незалежні змінні, символічно записуються у вигляді формули

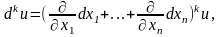
яка формально розкривається за біномним законом.

Зокрема, у випадку функції двох змінних 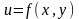, маємо:

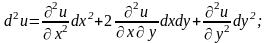
Градієнт функції 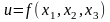- це вектор, що визначається формулою grad 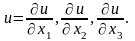Він визначає напрямок найшвидшого зростання функції:

Приклад 9. Нехай 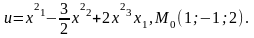Знайти grad u (M₀).

Маємо

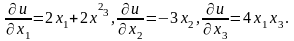
Тоді

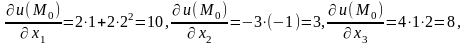
а тому grad u(M₀)= (10;3;8)=

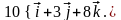
Реферат з математики

Тема: Неперервні функції

1. Неперервність функції в точці і на відрізку

х .

х = х2- х1.

у.

(x1) .

Тепер можна перейти до поняття неперервності функції. Дамо два означення

неперервності функції в точці, які досить часто використовуються.

(х) називають неперервною при х = х0 або в точці х0.

0.

(х) називають неперервною при х = х0, якщо:

(х) існує при х = х0 та в деякому околі точки х0;

;

незалежно від способу прямування х до х0,

.

Ця ознака нижче буде використана для класифікації точок розриву.

(х) неперервна в точці а справа.

(х) в точці х = b неперервна зліва.

(х) називають неперервною на відрізку [а,b].

2. Класифікація розривів функції

Якщо при деякому х = x1 будь-яка із умов неперервності означення 2 не

виконується, то кажуть, що функція в цій точці має розрив, а точку x1

називають точкою розриву функції (дивись Мал. 1.).

Поняття неперервності та розриву функції можна наочно показати на

графіку функції.

, тобто не існує скінченної границі.

Графік функції, що зображений на Малюнку 1 має розриви в точках х1 та х2

Розриви функції бувають ліквідовні та неліквідовні:

(х) не визначена в точці х, або визначена, але мають місце

співвідношення

то розрив в точці х1 називають ліквідовним. В цьому випадку функцію

можна визначити або змінити її значення в точці х, так, щоб виконувались

рівності

2) неліквідовні розриви поділяються на розриви першого та другого роду.

називають стрибком функції;

, то розрив в цій точці називають розривом другого роду.

На Малюнку 1 функція має розрив першого роду в точці х1, її стрибок

дорівнює b - а, а в точці х2 функція має розрив другого роди.

3. Властивості неперервних функцій та дії з ними

Приведемо без доведень властивості неперервних функцій.

(х) неперервна на відрізку [a, b], то вона обмежена на цьому відрізку,

тобто існують такі числа M та m, що

[а, b].

Теорема 2. Усі основні елементарні функції неперервні в кожній точці

своєї області існування.

Теорема 3. Алгебраїчна сума, добуток (скінченної кількості доданків та

множників) та частка функцій, неперервних при x = х0 (в останньому

випадку дільник в цій точці не повинен дорівнювати нулю) є також

неперервна функція при х = х0.

Теорема 4. Неперервна функція від неперервної функції є також неперервна

функція.

Теорема 5. Будь-яка елементарна функція неперервна в кожній точці своєї

області існування.