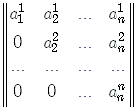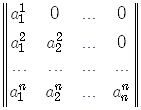[Ред.] Приклад

Матриця     є матрицею 4×3. Елемент A[2,3], або a_2,3 дорівнює 7.

1. Матрицю розміром усі елементи якої нулі, звуть нульовою матрицею (позначають

2. Якщо то матрицю звуть квадратною матрицею порядку Набір елементів утворює головну діагональ, а набір — побічну діагональ.

Приміром, матриця

— квадратна матриця 3-го порядку; елементи творять головну діагональ, а елементи — побічну.

3. Квадратну матрицю, всі елементи якої, нижче (вище) головної діагоналі дорівнюють нулеві, звуть верхньою (нижньою) трикутною матрицею (рис. 1.1).

Рис. 1.1

4. Квадратну матрицю, у якої всі елементи, крім, можливо, елементів головної діагоналі, дорівнюють нулеві, звуть діагональною матрицею (рис. 1.2).

Рис. 1.2

5. Діагональну матрицю порядку у якої всі елементи головної діагоналі дорівнюють одиниці, звуть одиничною матрицею і позначають

Приміром,

6. Матрицю розміром звуть матрицею-рядком ( рядком) завдовжки

7. Матрицю розміром звуть матрицею-стовпцем ( стовпцем) заввишки

6. Траспонована матриця

Транспонована матриця — матриця , що виникає з матриці в результаті унарної операції транспонування: заміни її рядків на стовпчики.

Формально, транспонована матриця для матриці визначається як

Наприклад:

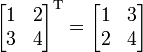     та     

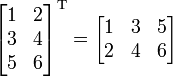
7. Обернена матриця

Обернена матриця — для кожної невиродженої квадратної матриці , розмірності , завжди існує обернена матриця, позначається така що:

де одинична матриця.

Якщо для матриці існує , то така матриця називається оборотною, тобто кожна невироджена матриця є оборотною, і навпаки кожна оборотна матриця є невиродженою.

8. Операції над матрицями

Перш за все, домовимося вважати дві матриці рівними, якщо ці матриці мають однакові порядки і всі їх відповідні елементи збігаються. Перейдемо до визначення основних операції над матрицями. Додавання матриць. Сумою двох матриць A = | | a _ij | |, Де (i = 1, 2, ..., т, j = 1, 2, ..., n) і В = | | b _ij | |, Де (i = 1, 2, ..., т, j = 1, 2, ..., n) одних і тих же порядків т і п називається матриця С = | | c _ij | | (І = 1,2, ..., т; j = 1, 2, ...., п) тих же порядків т і п, елементи з _ij якої визначаються за формулою , Де (i = 1, 2, ..., т, j = 1, 2, ..., n) (1.2) Для позначення суми двох матриць використовується запис С = А + В. Операція складання суми матриць називається їх складанням. Отже, за визначенням: + = 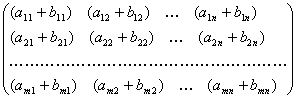З визначення суми матриць, а точніше з формул (1.2) безпосередньо випливає, що операція додавання матриць має ті ж властивості, що й операція додавання речовинний-них чисел, а саме: 1) переместительное властивістю: А + В = В + А, 2) сполучним властивістю: (A + B) + С = А + (В + С). Ці властивості дозволяють не дбати про порядок проходження доданків матриць при складанні двох або більшої кількості матриць. Множення матриці на число. Твором матриці A = | | a _ij | |, Де (i = 1, 2, ..., m, j = 1, 2, ..., n) на дійсне число l, називається матриця С = | | c _ij | | (І = 1,2, ..., m; j = 1, 2, ...., n), елементи якої визначаються за формулою: , Де (i = 1, 2, ..., т, j = 1, 2, ..., n) (1.3) Для позначення твори матріциі на число використовується запис С = l A або С = А l. Операція складання твору матриці на число називається множенням матриці на це число. Безпосередньо з формули (1.3) ясно, що множення матриці на число має такі властивості: 1) сполучним властивістю щодо числового множника: (l m) A = l (m A); 2) розподільчим властивістю щодо суми матриць: l (A + B) = l A + l B; 3) розподільчим властивістю щодо суми чисел: (l + m) A = l A + m A Зауваження. Різницею двох матриць А і В однакових порядків т і п природно назвати таку матрицю З тих же порядків т і п, яка в сумі з матрицею B дає матрицю A. Для позначення різниці двох матриць використовується природна запис: С = A - В. Дуже легко переконатися в тому, що різниця З двох матриць А і В може бути отримана за правилом С = A + (-1) В. Твір матриць або перемножування матриць. Твором матриці A = | | a _ij | |, Де (i = 1, 2, ..., m, j = 1, 2, ..., n) має порядки, відповідно рівні т і n, на матрицю В = | | b _ij | |, Де (i = 1, 2, ..., n, j = 1, 2, ..., р), що має порядки, відповідно рівні n і р, називається матриця С = | | c _ij | | (І = 1,2, ..., m; j = 1, 2, ...., р), що має порядки, відповідно рівні т і р елементи якої визначаються-ються за формулою: де (i = 1, 2, ..., m, j = 1, 2, ..., p) (1.4) Для позначення твори матріциі А на матрицю В використовують запис С = А × В. Операція складання твору матриці А на матрицю В називається перемножуванням цих матриць. З сформульованого вище визначення випливає, що матрицю А можна помножити не на всяку матрицю В, необхідно, щоб число стовпців матриці А було дорівнює числу рядків матриці В. Формула (1.4) являє собою правило складання елементів матриці С, що є твором матриці А на матрицю В. Це правило можна сформулювати і словесно: елемент c _{i j} стоїть на пвресеченіі і-го рядка і j-го стовпця матріцьі С = А В, дорівнює сумі попарних творів відповідних елементів і-го рядка матриці А і j-го стовпця матриці В. Як приклад застосування зазначеного правила наведемо формулу множення квадратних матриць другого порядку. × 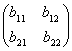= 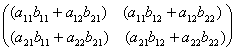З формули (1.4) випливають такі властивості твори матриці А на Матрі-цу В: 1) сочетательное властивість: (А В) С = А (В С); 2) розподільне щодо суми матриць властивість: (A + B) С = О З + В С або A (В + С) = A В + А С. Питання про перестановною (переместительное) властивості твори матриці A на матрицю В має сенс ставити лише для квадратних матриць A і В однакового порядку. Наведемо важливі приватні випадки матриць, для яких справедливо і переста-новочное властивість. Дві матриці для твори яких справедливо перестановочне властивість, прийнято називає коммутирующими. Серед квадратних матриць виділимо клас так званих діагональних матриць, у кожної з яких елементи, розташовані поза головної діагоналі, дорівнюють нулю. Кожна діа-класичної теорії ортогональних матриця порядку п має вигляд D = 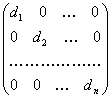(1.5) де d _1, d _2, ..., d _n-які завгодно числа. Легко бачити, що якщо всі ці числа рівні між собою, тобто d ₁ = d ₂ = ... = d _n то для будь-квадратної матриці А порядку п справедливо рівність А D = D А. Серед всіх діагональних матриць (1.5) з збігаються елементами d ₁ = d ₂ = ... = d _n = = D особливо важливу роль відіграють дві матриці. Перша з цих матриць виходить при d = 1, називається одиничною матрицею n-го порядку і позначається символом Є. Друга матриця виходить при d = 0, називається нульовою матрицею n-го порядку і позначається символом O. Таким чином, E = O = У силу доведеного вище А Е = Е А і А О = О А. Більше того, легко показати, що А Е = Е А = А, А О = О А = 0. (1.6) Перша з формул (1.6) характеризує особливу роль одиничної матриці Е, аналогічну тій ролі, яку відіграє число 1 при перемноження дійсних чисел. Що ж стосується особливої ​​ролі нульової матриці О, то її виявляє не тільки друга з формул (1.7), але й елементарно перевіряється рівність А + 0 = 0 + А = А. На закінчення зазначимо, що поняття нульової матриці можна вводити і для неквадрат-них матриць (нульовий називають будь-яку матрицю, всі елементи якої равниї нулю).