
№2.1
С![]()
![]()
![]()
![]() татистический
метод —
это метод исследования систем из большого
числа частиц, оперирующий статистическими
закономерностями
и средними
(усредненными)
значениями физических величин,
характеризующих всю систему.
Термодинамический
метод —
это метод исследования систем из большого
числа частиц, оперирующий величинами,
характеризующими систему
в целом (например,
давление, объем, температура)
при различных превращениях энергии,
происходящих в системе, не учитывая при
этом внутреннего строения изучаемых
тел и характера движения отдельных
частиц. Молекулярная
физика —
раздел физики, изучающего строение и
свойства вещества исходя
из
молекулярно-кинетических представлений,
основывающихся на том, что все
тела состоят из атомов, молекул или
ионов находящихся в непрерывном
хаотическом движении.
термодинамическая
система —
совокупность макроскопических тел,
которые взаимодействуют и обмениваются
энергией как между собой, так и с другими
телами (внешней средой). Любое изменение
в
термодинамической системе, связанное
с изменением хотя бы одного из ее
термодинамических параметров, называется
термодинамическим
процессом.
Состояние системы задается термодинамическими
параметрами (параметрами
состояния)
—
совокупностью физических величин,
характеризующих свойства термодинамической
системы. Обычно в качестве параметров
состояния выбирают температуру,
давление и объем.
Уравнением
состояния термодинамической
системы называется уравнение, которое
связывает давление p
,
объем V
и
температуру T
термодинамической
системы, находящейся в состоянии
термодинамического равновесия.
Идеальный газ
- это газ, в котором отсутствуют силы
межмолекулярного взаимодействия, т .
е. молекулы считаются упругими твердыми
шариками соударения между которыми
абсолютно упругие, силы притяжения межу
ними отсутствуют.
Физическая
модель,
идеального газа 1) собственный
объем
молекул газа пренебрежимо
мал
по сравнению с объемом сосуда; 2) между
молекулами газа отсутствуют силы
взаимодействия;
3) столкновения
молекул
газа между собой и со стенками сосуда
абсолютно
упругие.
Закон
Дальтона:
давление
смеси идеальных газов равно сумме
парциальных давлений n
входящих в нее газов.
Парциальное
давление —
давление, которое производил бы газ,
входящий в состав газовой смеси, если
бы он один занимал объем, равный объему
смеси при той же температуре. Закон
Бойля-Мариотта:
Для данной массы газа m
при постоянной температуре T
произведение давления p
на объем V
есть величина постоянная: PV=const.
Закон
Гей-Люссака: Давление
p
данной массы m
газа при постоянном объеме изменяется
линейно с температурой t
.
Объем
V
данной массы m
газа при постоянном давлении изменяется
линейно с температурой t.
татистический
метод —
это метод исследования систем из большого
числа частиц, оперирующий статистическими
закономерностями
и средними
(усредненными)
значениями физических величин,
характеризующих всю систему.
Термодинамический
метод —
это метод исследования систем из большого
числа частиц, оперирующий величинами,
характеризующими систему
в целом (например,
давление, объем, температура)
при различных превращениях энергии,
происходящих в системе, не учитывая при
этом внутреннего строения изучаемых
тел и характера движения отдельных
частиц. Молекулярная
физика —
раздел физики, изучающего строение и
свойства вещества исходя
из
молекулярно-кинетических представлений,
основывающихся на том, что все
тела состоят из атомов, молекул или
ионов находящихся в непрерывном
хаотическом движении.
термодинамическая
система —
совокупность макроскопических тел,
которые взаимодействуют и обмениваются
энергией как между собой, так и с другими
телами (внешней средой). Любое изменение
в
термодинамической системе, связанное
с изменением хотя бы одного из ее
термодинамических параметров, называется
термодинамическим
процессом.
Состояние системы задается термодинамическими
параметрами (параметрами
состояния)
—
совокупностью физических величин,
характеризующих свойства термодинамической
системы. Обычно в качестве параметров
состояния выбирают температуру,
давление и объем.
Уравнением
состояния термодинамической
системы называется уравнение, которое
связывает давление p
,
объем V
и
температуру T
термодинамической
системы, находящейся в состоянии
термодинамического равновесия.
Идеальный газ
- это газ, в котором отсутствуют силы
межмолекулярного взаимодействия, т .
е. молекулы считаются упругими твердыми
шариками соударения между которыми
абсолютно упругие, силы притяжения межу
ними отсутствуют.
Физическая
модель,
идеального газа 1) собственный
объем
молекул газа пренебрежимо
мал
по сравнению с объемом сосуда; 2) между
молекулами газа отсутствуют силы
взаимодействия;
3) столкновения
молекул
газа между собой и со стенками сосуда
абсолютно
упругие.
Закон
Дальтона:
давление
смеси идеальных газов равно сумме
парциальных давлений n
входящих в нее газов.
Парциальное
давление —
давление, которое производил бы газ,
входящий в состав газовой смеси, если
бы он один занимал объем, равный объему
смеси при той же температуре. Закон
Бойля-Мариотта:
Для данной массы газа m
при постоянной температуре T
произведение давления p
на объем V
есть величина постоянная: PV=const.
Закон
Гей-Люссака: Давление
p
данной массы m
газа при постоянном объеме изменяется
линейно с температурой t
.
Объем
V
данной массы m
газа при постоянном давлении изменяется
линейно с температурой t.
О![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() сновное:
Температура:
физическая
величина, характеризующая состояние
термодинамического равновесия
макроскопической системы и определяющая
направление теплообмена между телами.
Уравнение
состояния идеального газа:
Уравнение
Менделеева-Клапейрона:
Изотермический:
сновное:
Температура:
физическая
величина, характеризующая состояние
термодинамического равновесия
макроскопической системы и определяющая
направление теплообмена между телами.
Уравнение
состояния идеального газа:
Уравнение
Менделеева-Клапейрона:
Изотермический:
Изобарный: Изохорный:
№![]()
![]() 2.2
2.2
С![]()
![]()
![]() редняя:
Для системы, находящейся
в состоянии термодинамического равновесия
на каждую поступательную и вращательную
степень свободы приходится в среднем
кинетическая энергия, равная kT/2
, а на каждую колебательную степень
свободы — в среднем энергия, равная kT.
редняя:
Для системы, находящейся
в состоянии термодинамического равновесия
на каждую поступательную и вращательную
степень свободы приходится в среднем
кинетическая энергия, равная kT/2
, а на каждую колебательную степень
свободы — в среднем энергия, равная kT.
В![]() нутренняя
энергия идеального газа,
содержащего N
не
взаимодействующих молекул (общее
число степеней свободы iN):
нутренняя
энергия идеального газа,
содержащего N
не
взаимодействующих молекул (общее
число степеней свободы iN):
№2.3
К![]()
![]()
![]()
![]() оличество
энергии, передаваемой системе внешними
телами в форме теплоты, называется
количеством
теплоты
или теплотой Q
сообщаемой передаваемой системе. Первое
начало термодинамики – это закон
сохранения и превращения энергии
в термодинамических процессах.
:теплота,
сообщаемая системе, расходуется на
изменение ее внутренней энергии и на
совершение ею работы против внешних
сил.
Изотермический:
оличество
энергии, передаваемой системе внешними
телами в форме теплоты, называется
количеством
теплоты
или теплотой Q
сообщаемой передаваемой системе. Первое
начало термодинамики – это закон
сохранения и превращения энергии
в термодинамических процессах.
:теплота,
сообщаемая системе, расходуется на
изменение ее внутренней энергии и на
совершение ею работы против внешних
сил.
Изотермический:
![]()
![]()
![]()
![]()
![]() Изобарный:
Изохорный:
Адиабата:
Изобарный:
Изохорный:
Адиабата:
И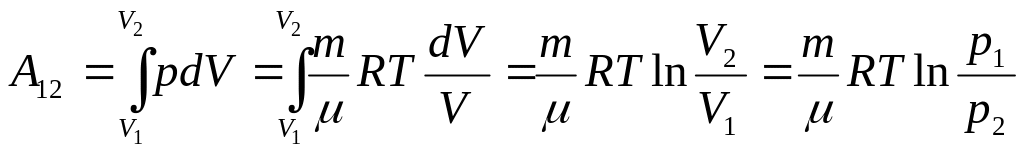 зотермический:
Изобарный:
зотермический:
Изобарный:
![]()
![]()
И![]()
![]() зохорный:
зохорный:
№2.4
В
![]()
![]()
![]()
![]()
![]()
![]()
![]() нутренняя
энергия
идеального газа, содержащего N
не взаимодействующих молекул (общее
число степеней свободы iN):
Теплоемкость
идеального газа в классической теории
не зависит от температуры.
В
экспериментах соответствует
только одноатомным газам.
нутренняя
энергия
идеального газа, содержащего N
не взаимодействующих молекул (общее
число степеней свободы iN):
Теплоемкость
идеального газа в классической теории
не зависит от температуры.
В
экспериментах соответствует
только одноатомным газам.
![]()
М![]()
![]() олярная
теплоемкость C
—
величина,
равная количеству теплоты, необходимому
для нагревания 1моль вещества на 1К.
Единица
молярной теплоемкости —
Дж/(моль
К).
Удельная
теплоемкость вещества c:
величина,
равная количеству теплоты, необходимому
для нагревания 1кг вещества на 1К. Единица
удельной теплоемкости —
Дж/(кг К).
олярная
теплоемкость C
—
величина,
равная количеству теплоты, необходимому
для нагревания 1моль вещества на 1К.
Единица
молярной теплоемкости —
Дж/(моль
К).
Удельная
теплоемкость вещества c:
величина,
равная количеству теплоты, необходимому
для нагревания 1кг вещества на 1К. Единица
удельной теплоемкости —
Дж/(кг К).
![]()
![]() Тепловая
энергия
сравнима с квантом колебательной
Тепловая
энергия
сравнима с квантом колебательной
![]()
![]()
![]()
![]()
энергии: Тепловая энергия сравнима с квантом вращательной энергии:
№2.5
А![]()
![]()
![]()
![]()
 диабатическим
называется
процесс, при котором отсутствует
теплообмен между
системой и окружающей средой (δQ
= 0 ).
Уравнения
Пуассона:
Коэффициент
Пуассона:
диабатическим
называется
процесс, при котором отсутствует
теплообмен между
системой и окружающей средой (δQ
= 0 ).
Уравнения
Пуассона:
Коэффициент
Пуассона:
З![]()
![]()
![]() акон:
Процесс,
в котором теплоемкость остается
постоянной называется политропическим.
акон:
Процесс,
в котором теплоемкость остается
постоянной называется политропическим.
Уравнение политропы: Показатель политропы:
№2.6
Состояние газа характеризуется p, V, T: макроскопическими параметрами. Описание системы внешними и внутренними параметрами. Внутренние параметры: состояние молекул газа. Состояние системы характеризующиеся положением и скоростями всех её молекул: микроскопическая. Статистическим ансамблем физической системы называется набор всевозможных состояний данной системы, отвечающих определённым критериям. Микроканонический ансамбль, описывающий состояния системы с заданными (постоянными) энергией, импульсом и моментом импульса системы.
П![]() остулат
равновероятности: все
микроскопические состояния системы
равновероятны. Эргодическая
гипотеза: средняя
величина, характеризующая частицу
рассчитанная по числу её возможных
состояний равна среднему значению этой
величины усреднённому за достаточно
большой промежуток времени. Термодинамическая
вероятность
состояния тела или системы: это
число способов, которыми может быть
реализовано данное конкретное
термодинамическое состояние
(макросостояние).
Иначе говоря, это число всевозможных
микрораспределений
частиц
по координатам и скоростям (микросостояний),
которыми может быть осуществлено данное
макросостояние.
остулат
равновероятности: все
микроскопические состояния системы
равновероятны. Эргодическая
гипотеза: средняя
величина, характеризующая частицу
рассчитанная по числу её возможных
состояний равна среднему значению этой
величины усреднённому за достаточно
большой промежуток времени. Термодинамическая
вероятность
состояния тела или системы: это
число способов, которыми может быть
реализовано данное конкретное
термодинамическое состояние
(макросостояние).
Иначе говоря, это число всевозможных
микрораспределений
частиц
по координатам и скоростям (микросостояний),
которыми может быть осуществлено данное
макросостояние.
г![]() де
Го-
число возможных микросостояний.
Флуктуации
— случайные отклонения от среднего
значения физических величин, характеризующих
систему из большого числа частиц. Можно
показать, что чем больше частиц в системе,
тем большие флуктуации менее вероятны:
де
Го-
число возможных микросостояний.
Флуктуации
— случайные отклонения от среднего
значения физических величин, характеризующих
систему из большого числа частиц. Можно
показать, что чем больше частиц в системе,
тем большие флуктуации менее вероятны:
где М- число частиц в системе.
№2.7
Р![]()
![]()
![]()
![]() аспределение
вероятностей
— это закон, описывающий область значений
случайной
величины
и вероятности их принятия. В газе,
находящемся в состоянии равновесия при
данной температуре, устанавливается
некоторое стационарное, не меняющееся
со временем распределение молекул по
скоростям. Это распределение описывается
функцией f
(v),
называемой функцией
распределения молекул по скоростям:
аспределение
вероятностей
— это закон, описывающий область значений
случайной
величины
и вероятности их принятия. В газе,
находящемся в состоянии равновесия при
данной температуре, устанавливается
некоторое стационарное, не меняющееся
со временем распределение молекул по
скоростям. Это распределение описывается
функцией f
(v),
называемой функцией
распределения молекул по скоростям:
Средняя скорость молекулы газа:
![]()
![]()
Н![]()
![]()
![]() аиболее
вероятная скорость молекул идеального
газа: Средняя
квадратичная скорость:
аиболее
вероятная скорость молекул идеального
газа: Средняя
квадратичная скорость:
№![]()
![]() 2.8
2.8
Ф ормула:
:такое
распределение называют распределением
Больцмана
(распределение
частиц по значениям потенциальной
энергии) для внешнего потенциального
поля.
Распределение
Максвелла-Больцмана:
где dn:
количество молекул в единице объёма, и
имеющих Еп
, а Ек
лежит
в интервале от Ек
до
Ек+dЕк
.
Если частицы имеют одинаковую массу и
находятся в состоянии хаотического
теплового движения, то распределение
Больцмана справедливо в любом внешнем
потенциальном поле, а не только в поле
сил тяжести.
ормула:
:такое
распределение называют распределением
Больцмана
(распределение
частиц по значениям потенциальной
энергии) для внешнего потенциального
поля.
Распределение
Максвелла-Больцмана:
где dn:
количество молекул в единице объёма, и
имеющих Еп
, а Ек
лежит
в интервале от Ек
до
Ек+dЕк
.
Если частицы имеют одинаковую массу и
находятся в состоянии хаотического
теплового движения, то распределение
Больцмана справедливо в любом внешнем
потенциальном поле, а не только в поле
сил тяжести.
№2.9
Э![]()
![]() нтропия
является мерой неупорядоченности
системы,
—
чем больше число микросостояний,
реализующих данное макросостояние, тем
больше энтропия. Все
процессы в замкнутой системе ведут к
увеличению её энтропии. В
замкнутой системе идут в направлении
от
менее вероятных состояний
к
более вероятным,
до тех пор, пока вероятность состояния
не станет максимальной. В состоянии
равновесия — наиболее вероятного
состояния системы — число микросостояний
максимально, при этом максимальна и
энтропия. Неравенство
Клаузиуса:
энтропия замкнутой системы может либо
возрастать (в случае необратимых
процессов) либо оставаться постоянной
(в случае обратимых процессов).
нтропия
является мерой неупорядоченности
системы,
—
чем больше число микросостояний,
реализующих данное макросостояние, тем
больше энтропия. Все
процессы в замкнутой системе ведут к
увеличению её энтропии. В
замкнутой системе идут в направлении
от
менее вероятных состояний
к
более вероятным,
до тех пор, пока вероятность состояния
не станет максимальной. В состоянии
равновесия — наиболее вероятного
состояния системы — число микросостояний
максимально, при этом максимальна и
энтропия. Неравенство
Клаузиуса:
энтропия замкнутой системы может либо
возрастать (в случае необратимых
процессов) либо оставаться постоянной
(в случае обратимых процессов).
В![]()
![]()
![]()
![]()
![]() торое
начало термодинамики:
система
представленная сама себе движется в
сторону более равновесного состояния,
т.е. энтрапия максимальна.
Любой
необратимый процесс в замкнутой системе
происходит так, что энтропия системы
при этом возрастает (закон
возрастания энтропии):
Третье
начало термодинамики
—
теорема
Нернста–Планка —
постулирует поведение термодинамических
систем при нуле Кельвина (абсолютном
нуле): энтропия
всех тел в состоянии равновесия стремится
к нулю по мере приближения температуры
к нулю Кельвина.
торое
начало термодинамики:
система
представленная сама себе движется в
сторону более равновесного состояния,
т.е. энтрапия максимальна.
Любой
необратимый процесс в замкнутой системе
происходит так, что энтропия системы
при этом возрастает (закон
возрастания энтропии):
Третье
начало термодинамики
—
теорема
Нернста–Планка —
постулирует поведение термодинамических
систем при нуле Кельвина (абсолютном
нуле): энтропия
всех тел в состоянии равновесия стремится
к нулю по мере приближения температуры
к нулю Кельвина.
![]()
№2.10
Т![]()
![]()
![]()
![]() ермодинамический
процесс называется обратимым,
если он может происходить как в прямом,
так и в обратном направлении.
Причем, если такой процесс происходит
сначала в прямом, а затем в обратном
направлении и система возвращается в
исходное состояние, то в окружающей
среде и в этой системе не происходит
никаких изменений. Всякий процесс, не
удовлетворяющий этим условиям, является
необратимым.
Реальные процессы необратимы, в них
всегда происходит диссипация (потеря)
энергии (из-за трения, теплопроводности
и т.д.). Обратимые
процессы —
это
физическая модель —идеализация
реальных процессов.
Круговым
процессом (или
циклом)
называется процесс, при котором система,
пройдя через ряд состояний, возвращается
в исходное состояние. Работа
за цикл A
определяется
площадью, охватываемой замкнутой кривой.
КПД:
Обратный
цикл используется в холодильных
машинах
(за
счет работы внешних сил
теплота переносится к телу с более
высокой температурой).
Тепловой двигатель
— тепловая
машина,
превращающая тепло
в механическую энергию.
Теорема
Карно
КПД обратимых машин,
работающих при одинаковых температурах
нагревателей и холодильников, равны
друг другу и не
зависят от природы рабочего тела,
а определяются только температурами
нагревателя и холодильника. Наиболее
экономичный обратимый
круговой
процесс,
состоящий из двух изотерм и двух адиабат.
Из всех периодически действующих
тепловых
машин,
имеющих одинаковые
температуры
нагревателей T1
и холодильников T2,
наибольшим
КПД обладают
обратимые
машины.
ермодинамический
процесс называется обратимым,
если он может происходить как в прямом,
так и в обратном направлении.
Причем, если такой процесс происходит
сначала в прямом, а затем в обратном
направлении и система возвращается в
исходное состояние, то в окружающей
среде и в этой системе не происходит
никаких изменений. Всякий процесс, не
удовлетворяющий этим условиям, является
необратимым.
Реальные процессы необратимы, в них
всегда происходит диссипация (потеря)
энергии (из-за трения, теплопроводности
и т.д.). Обратимые
процессы —
это
физическая модель —идеализация
реальных процессов.
Круговым
процессом (или
циклом)
называется процесс, при котором система,
пройдя через ряд состояний, возвращается
в исходное состояние. Работа
за цикл A
определяется
площадью, охватываемой замкнутой кривой.
КПД:
Обратный
цикл используется в холодильных
машинах
(за
счет работы внешних сил
теплота переносится к телу с более
высокой температурой).
Тепловой двигатель
— тепловая
машина,
превращающая тепло
в механическую энергию.
Теорема
Карно
КПД обратимых машин,
работающих при одинаковых температурах
нагревателей и холодильников, равны
друг другу и не
зависят от природы рабочего тела,
а определяются только температурами
нагревателя и холодильника. Наиболее
экономичный обратимый
круговой
процесс,
состоящий из двух изотерм и двух адиабат.
Из всех периодически действующих
тепловых
машин,
имеющих одинаковые
температуры
нагревателей T1
и холодильников T2,
наибольшим
КПД обладают
обратимые
машины.
№2.11
Т![]()
![]()
![]() ермодинамические
потенциалы
(термодинамические
функции) —
функции основных макроскопических
параметров (температура, давление,
энтропия и т. д.)
термодинамической системы, характеризующие
её состояние.
Внутренняя энергия
определяется в соответствии с первым
началом термодинамики
как разность между количеством
теплоты,
сообщенным системе, и работой,
совершенной системой над
внешними телами.
ермодинамические
потенциалы
(термодинамические
функции) —
функции основных макроскопических
параметров (температура, давление,
энтропия и т. д.)
термодинамической системы, характеризующие
её состояние.
Внутренняя энергия
определяется в соответствии с первым
началом термодинамики
как разность между количеством
теплоты,
сообщенным системе, и работой,
совершенной системой над
внешними телами.
С![]()
![]()
![]()
![]()
![]()
![]()
![]() вободная
энергия: Энтальпия:
Потенциал
Гиббса: Соотношения Максвелла:
вободная
энергия: Энтальпия:
Потенциал
Гиббса: Соотношения Максвелла:
К![]()
![]()
![]()
![]() ритерии:
ритерии:
№2.12
Я![]()
![]()
![]()
![]()
![]() влениями
переноса называются
необратимые процессы в термодинамически
неравновесных системах,
в которых происходит пространственный
перенос энергии
теплопроводность),
массы
(диффузия),
импульса
(внутреннее
трение). Градиент:
Время релаксации
-промежуток времени, в течение которого
выведенная из равновесия система
возвращается в состояние термодинамического
равновесия.
Путь,
который в среднем проходят молекулы
между двумя последовательными
столкновениями называется средней
длиной свободного пробега молекул.
Эффективное
сечение: среднее число
столкновений,
испытываемых одной молекулой газа за
1с:
влениями
переноса называются
необратимые процессы в термодинамически
неравновесных системах,
в которых происходит пространственный
перенос энергии
теплопроводность),
массы
(диффузия),
импульса
(внутреннее
трение). Градиент:
Время релаксации
-промежуток времени, в течение которого
выведенная из равновесия система
возвращается в состояние термодинамического
равновесия.
Путь,
который в среднем проходят молекулы
между двумя последовательными
столкновениями называется средней
длиной свободного пробега молекул.
Эффективное
сечение: среднее число
столкновений,
испытываемых одной молекулой газа за
1с:
Т![]() еплопроводность:
если
в одной области газа средняя кинетическая
энергия молекул больше, чем в другой,
то с течением времени вследствие
постоянных столкновений молекул
происходит процесс выравнивания средних
кинетических энергий молекул —
выравнивание температур. Явление
диффузии заключается
в том, что происходит самопроизвольное
проникновение и перемешивание частиц
двух соприкасающихся газов, жидкостей
и даже твердых тел; диффузия сводится
к обмену частицами (перенос масс) между
этими телами, возникает и продолжается,
пока существует градиент
плотности.
Внутреннее
трение (вязкость).
Вследствие хаотического теплового
движения молекул происходит обмен
молекулами между слоями газа движущимися
с различными скоростями, в результате
чего импульс слоя, движущегося быстрее,
уменьшается, а движущегося медленнее
— увеличивается (происходит перенос
импульса от
одного слоя к другому). Это приводит к
торможению слоя, движущегося быстрее,
и ускорению слоя, движущегося медленнее.
еплопроводность:
если
в одной области газа средняя кинетическая
энергия молекул больше, чем в другой,
то с течением времени вследствие
постоянных столкновений молекул
происходит процесс выравнивания средних
кинетических энергий молекул —
выравнивание температур. Явление
диффузии заключается
в том, что происходит самопроизвольное
проникновение и перемешивание частиц
двух соприкасающихся газов, жидкостей
и даже твердых тел; диффузия сводится
к обмену частицами (перенос масс) между
этими телами, возникает и продолжается,
пока существует градиент
плотности.
Внутреннее
трение (вязкость).
Вследствие хаотического теплового
движения молекул происходит обмен
молекулами между слоями газа движущимися
с различными скоростями, в результате
чего импульс слоя, движущегося быстрее,
уменьшается, а движущегося медленнее
— увеличивается (происходит перенос
импульса от
одного слоя к другому). Это приводит к
торможению слоя, движущегося быстрее,
и ускорению слоя, движущегося медленнее.
№![]() 2.13
2.13
![]()
![]()
![]()
![]()
![]() Перенос
энергии (в
форме теплоты) описывается законом
Фурье.
Коэффициент
теплопроводности:
Уравнение
Фурье: Перенос
массы (диффузия)
для химически
однородного газа
подчиняется закону Фика:
Коэффициент
диффузии:
Перенос
энергии (в
форме теплоты) описывается законом
Фурье.
Коэффициент
теплопроводности:
Уравнение
Фурье: Перенос
массы (диффузия)
для химически
однородного газа
подчиняется закону Фика:
Коэффициент
диффузии:
З![]()
![]()
![]() акон
Фика:
Формулы для
коэффициентов λ,
D
и η
связывают
коэффициенты
переноса и характеристики
теплового движения молекул:
акон
Фика:
Формулы для
коэффициентов λ,
D
и η
связывают
коэффициенты
переноса и характеристики
теплового движения молекул:
Внутреннее трение(вязкость) описывается законом Ньютона:
