
- •Механика 1-3
- •2) Инерциальные системы отсчета. Принцип инерции, принципы относительности. Первый закон Ньютона. Сила. Основные силы в классической механике.
- •3)Второй закон Ньютона. Масса. Импульс. Третий закон Ньютона. Закон сохранения импульса.
- •Законы Кеплера. Солнечная система. Закон Всемирного тяготения. Гравитационные силы. Гравитационная и инертная массы, их эквивалентность. Черные дыры.
- •Гравитационное поле Земли. Сила тяжести. Вес. Невесомость. Космические скорости. Геоид. Аномалии ускорения силы тяжести. Принципы гравиразведки.
- •Силы трения покоя, скольжения и качения. Движение жидкости. Уравнение Бернулли. Вязкое трение, вязкость. Закон Стокса. Аэродинамика и природопользование.
- •Неинерциальные системы отсчета. Силы инерции. Перегрузки. Центробежная сила инерции. Зависимость веса тела от широты местности. Центрифуги. Сила Кориолиса.
- •Движения тела с переменной массой. Реактивное движение. Формула Циолковского. Уравнение Мещерского.
- •Работа силы. Мощность. Энергия. Кинетическая и потенциальная энергии. Консервативная система. Закон сохранения и превращения энергии. Энергия сжатой или растянутой пружины.
- •Центр масс системы материальных точек. Центральный удар. Упругое и неупрогое соударение двух тел.
- •Молекулярная физика и термодинамика.
- •2. Температура. Нулевое начало термодинамики. Экспериментальные газовые законы. Уравнение Менделеева-Клапейрона. Степени свободы.
- •Изопроцесс, протекающий в газе, при котором объем остается постоянным, называется изохорным.
- •Здесь p – давление газа при температуре t, °с; p0 – его давление при 0 °с.
- •3. Термодинамические процессы; графическое изображение процессов. Направленные процессы. Примеры термодинамических процессов.
- •4. Внутренняя энергия. Циклические процессы. Работа и теплота. Первое начало термодинамики.
- •6. Адиабатический процесс. Обратимые и необратимые термодинамические процессы. Тепловые машины. Цикл Карно. Кпд. Приведенная теплота.
- •7. Энтропия. Энтропия в обратимых и необратимых адиабатических процессах. Второе начало термодинамики.
- •8. Закон возрастания энтропии. Статистический смысл энтропии. Границы применимости второго начала термодинамики, «тепловая смерть» Вселенной. Третье начало термодинамики (уравнение Нернста).
- •10. Барометрическая формула. Явления переноса. Длина свободного пробега. Теплопроводность. Внутреннее трение (вязкость). Диффузия. Вакуум; ултраразреженные газы.
- •11. Реальные газы. Уравнение Ван-Дер-Ваальса. Изотермы Ван-Дер-Ваальса. Критическое состояние газа.
- •13. Твердые тела. Аморфные тела. Поли- и монокристаллы. Дефекты в кристаллах. Закон Дюлонга и Пти.
3. Термодинамические процессы; графическое изображение процессов. Направленные процессы. Примеры термодинамических процессов.
Термодинамический процесс — переход термодинамической системы из одного состояния в другое, который всегда связан с нарушением равновесия системы.
Адиабатический процесс — термодинамический процесс в макроскопической системе, при котором система не обменивается тепловой энергией с окружающим пространством. Адиабатический процесс для идеального газа описывается уравнением Пуассона. Линия, изображающая адиабатный процесс на термодинамической диаграмме, называется адиабатой. Адиабатическими можно считать процессы в целом ряде явлений природы. Так же такие процессы получили ряд применений в технике.

Изотермический процесс — термодинамический процесс, происходящий в физической системе при постоянной температуре. К изотермическим процессам относятся, например, кипение жидкости или плавление твёрдого тела при постоянном давлении. Графиком изотермического процесса является изотерма.
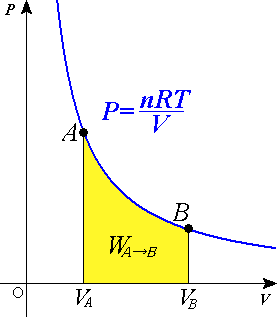
изобарный процесс — термодинамический процесс, происходящий в системе при постоянном давлении и постоянной массе идеального газа.
Согласно
закону
Гей-Люссака, при изобарном процессе
в идеальном
газе
![]() .
.
Работа,
совершаемая газом при расширении или
сжатии газа, равна
![]() .
.
Количество
теплоты, получаемое или отдаваемое
газом, характеризуется изменением
энтальпии:
![]() .
.

4. Внутренняя энергия. Циклические процессы. Работа и теплота. Первое начало термодинамики.
Внутренняя энергия тела (обозначается как E или U) — это сумма энергий молекулярных взаимодействий и тепловых движений молекулы. Внутренняя энергия является однозначной функцией состояния системы. Это означает, что всякий раз, когда система оказывается в данном состоянии, её внутренняя энергия принимает присущее этому состоянию значение, независимо от предыстории системы. Следовательно, изменение внутренней энергии при переходе из одного состояния в другое будет всегда равно разности между ее значениями в конечном и начальном состояниях, независимо от пути, по которому совершался переход.
Внутреннюю энергию тела нельзя измерить напрямую. Можно определить только изменение внутренней энергии:
![]()
Работа – одна из форм обмена энергией (наряду с теплотой) термодинамической системы с окружающими телами или количественная характеристика преобразованной энергии в физических процессах. Работа положительна, если она отдает энергию и отрицательна, если получает.
Теплота - кинетическая часть внутренней энергии вещества, определяемая интенсивным хаотическим движением молекул и атомов, из которых это вещество состоит. Мерой интенсивности движения молекул является температура. Количество теплоты, которым обладает тело при данной температуре, зависит от его массы.
Первое начало термодинамики - термодинамическая система может совершать работу только за счёт своей внутренней энергии или каких-либо внешних источников энергии. Первое начало термодинамики часто формулируют как невозможность существования вечного двигателя первого рода, который совершал бы работу, не черпая энергию из какого-либо источника.
5. Теплоемкость. Закон Джоуля. Физический смысл универсальной газовой постоянной. Формула Майера. Энтальпия термодинамической системы. Теплоемкости одноатомных и многоатомных газов. Отношение теплоемкостей.
Теплоемкость – физическая величина, определяющая отношение бесконечно малого количества теплоты δQ, полученного телом, к соответствующему приращению его температуры δT:
![]()
Закон Джоуля. Внутренняя энергия идеального газа зависит только от температуры и не зависит от его плотности.
Физический смысл универсальной газовой постоянной. УГЗ численно равна работе (расширению), которую совершает 1 моль идеального газа при его нагревании на 1 К при р=const. Таким образом для одного моля идеального одноатомного газа выполняется (формула Майера):
![]()
Первое больше второго по 1 началу термодинамики.
Энтальпия или энергия расширенной системы Е равна сумме внутренней энергии газа U и потенциальной энергии поршня с грузом Eпот = pSx = pV
![]()
Таким образом, энтальпия в данном состоянии представляет собой сумму внутренней энергии тела и работы, которую необходимо затратить, чтобы тело объёмом V ввести в окружающую среду, имеющую давление р и находящуюся с телом в равновесном состоянии. Энтальпия системы H — аналогично внутренней энергии и другим термодинамическим потенциалам — имеет вполне определенное значение для каждого состояния, т. е. является функцией состояния. Следовательно, в процессе изменения состояния.
Так
как энергия одной молекулы идеального
газа
![]() ,
то внутренняя
энергия одного моля
идеального газа равна:
,
то внутренняя
энергия одного моля
идеального газа равна:
|
|
|
|
то есть
|
|
|
(4.3.1) |
Внутренняя энергия произвольного количества газа:
|
|
|
(4.3.2) |
Её изменение:
|
|
|
|
Теплоёмкости одноатомных газов СV и СР
|
|
|
|
где теплоемкость при постоянном объеме СV – величина постоянная, от температуры не зависит. Учитывая физический смысл R для изобарических процессов, можно записать:
|
|
|
(4.3.3) |
Тогда теплоемкость при постоянном давлении для одноатомных газов:
|
|
или |
|
Полезно знать соотношение:
|
|
|
(4.3.4) |
где
γ - коэффициент
Пуассона,
![]() Так как
Так как
![]() , то
, то ![]() .
Из этого следует, что
.
Из этого следует, что
|
|
|
(4.3.5) |
Кроме
того,
![]() ,
где i
– число степеней свободы молекул.
Подставив в
выражение для внутренней энергии,
получим:
,
где i
– число степеней свободы молекул.
Подставив в
выражение для внутренней энергии,
получим:
|
|
|
|
Так
как
![]() ,
то внутреннюю
энергию можно найти по формуле
,
то внутреннюю
энергию можно найти по формуле
|
|
|
(4.3.6) |
То,
что
![]() ,
хорошо подтверждается на опыте с Ne, He,
Ar, Kr, парами одноатомных металлов.
Теплоемкости
многоатомных газов
Опыты с двухатомными газами, такими как
азот, кислород и др., показали, что
,
хорошо подтверждается на опыте с Ne, He,
Ar, Kr, парами одноатомных металлов.
Теплоемкости
многоатомных газов
Опыты с двухатомными газами, такими как
азот, кислород и др., показали, что
|
|
|
|
Для водяного пара и других многоатомных газов (СН3, СН4 и так далее)
|
|
|
|
Таким образом, молекулы многоатомных газов нельзя рассматривать как материальные точки. Необходимо учитывать вращательное движение молекул и число степеней свободы этих молекул. Числом степени свободы (i) называется число независимых переменных, определяющих положение тела в пространстве. Положение одноатомной молекулы, как и материальной точки, задаётся тремя координатами, поэтому она имеет три степени свободы (рис. 4.3).
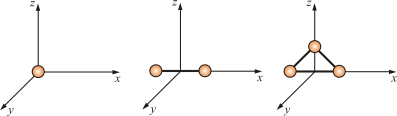 Рис.
4.3
Рис.
4.3
Многоатомная молекула может ещё и вращаться. Например, у двухатомных молекул вращательное движение можно разложить на два независимых вращения, а любое вращение можно разложить на три вращательных движения вокруг взаимно перпендикулярных осей. Но для двухатомной молекулы вращение вокруг её собственной оси не изменит её положение в пространстве, а момент инерции относительно этой оси равен нулю (рис. 4.3). Таким образом, у двухатомных молекул пять степеней свободы (i = 5), а у трёхатомных шесть степеней свободы (i = 6).
При
взаимных столкновениях молекул возможен
обмен их энергиями и превращение энергии
вращательного движения в энергию
поступательного движения и обратно.
Таким путём было установлено равновесие
между значениями средних энергий
поступательного и вращательного движения
молекул. Больцман
доказал,
что для не слишком низких температур
средняя
энергия
![]() ,
приходящаяся на одну степень свободы,
равна
,
приходящаяся на одну степень свободы,
равна
![]()
