Білет 4
Основні положення статики плоскої системи сил. Напрямок і величина зосередженої сили. Рівнодійна сила збіжної системи сил і поняття врівноважувальної сили.
Системою сил ( F1,F2 ,...Fn ) називають сукупність декількох сил, що діють на одне тіло або на систему тіл. Зрівноваженою називають таку систему сил, яка не змінює кінематичного стану твердого тіла. Така система сил еквівалентна нулю:
(F1,F2 ,...Fn) ~0.
Еквівалентними називають такі дві системи сил, які, діючи окремо на вільне тверде тіло, однаково змінюють його кінематичні характеристики (швидкість, напрямок руху і т.ін.).
Рівнодіючою силою R* даної системи сил називають таку силу, дія якої на тверде тіло або матеріальну точку еквівалентна дії цієї системи сил, тобто
R*~ (F1,F2 ,...Fn )
Плоскою системою сил називають таку систему сил, лінії дій яких лежать в одній площині.
1.3. Так як система збіжних сил зводиться до рівнодіючої, то для її рівноваги необхідно і достатньо, щоб ця рівнодіюча дорівнювала нулю:
R = 0
За умови, що R = 0 кінець вектора останньої сили системи при побудові силового многокутника співпаде з початком вектора першої сили. Звідси можна зробити висновок: система збіжних сил буде знаходитись у стані рівноваги тоді і тільки тоді, коли силовий многокутник цієї системи сил буде замкнутим. для рівноваги системи збіжних сил необхідно і достатньо, щоб сума проекцій всіх сил системи на кожну з трьох осей координат дорівнювала нулю.
У випадку плоскої системи збіжних сил використовують тільки два з трьох рівнянь рівноваги:
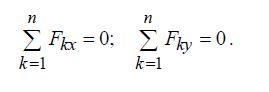
Якщо система сил має рівнодіючу, то сила Q , яка дорівнює рівнодіючій за модулем і направлена вздовж тієї ж лінії дії в протилежному напрямку, називається врівноважуючою. Додавання врівноважуючої сили Q до системи сил (F1,F2 ,...Fn)робить одержану нову систему сил зрівноваженою:
(F1,F2 ,...Fn ,Q)~0.
Зосереджена сила, це сила прикладена до однієї точки. Вона обирається модулем сили, - це позитивна скалярна величина, яка вимірюється в системі Сі в ньютонах, напрямком і точкою докладання. Зосереджена сила описується як векторна величина.
Статично невизначені системи при розтягу-стиску. Рівняння сумісності деформацій.
2.1. Статично невизначеними називаються такі конструкції, в елементах яких за допомогою тільки одних рівнянь статики визначити зусилля неможливо. Крім рівнянь статики для розрахунку таких систем (конструкцій) необхідно використовувати також рівняння, що містять деформації елементів конструкцій.
Схеми деяких статично невизначених конструкцій зображені на рис.5.11: а - стрижнева підвіска; б - стрижень, закріплений обома кінцями; в - стрижневий кронштейн; г - складне кільце; д - залізобетонна колона; е - шарнірно-стрижнева система.
а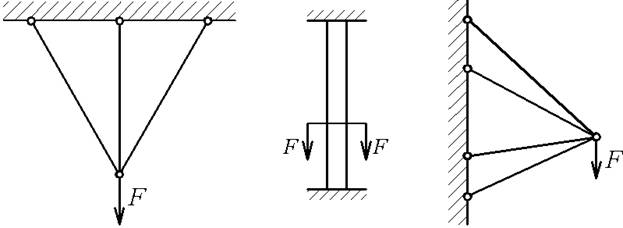
в
г
е
Рис.5.11. Приклади статично невизначених конструкцій
Всі статично невизначені конструкції мають додаткові, або так звані «зайві», зв'язки у вигляді закріплень, стрижнів або інших елементів. Зайвими такого зв'язку називають тому, що вони не є безумовно необхідними для забезпечення рівноваги конструкції і її геометричної незмінюваності, хоча постановка їх диктується умовами експлуатації. За умовами міцності і жорсткості конструкції зайві зв'язки можуть виявитися необхідними.
У статично невизначених конструкціях число невідомих, підлягаючих визначенню, більше, ніж число рівнянь статики, які можуть бути для цієї мети використані. Різниця між числом невідомих і числом рівнянь статики визначає число зайвих невідомих, або ступінь статичної невизначеності конструкції. При одній зайвій невідомій конструкція називається один раз статично невизначеною, при двох - двічі статично невизначеною і т.д. Конструкції, зображені на рис.5.11,а,б, г-е, що мають по одному додатковому зв'язку, є один раз статично невизначеними, а конструкція, представлена на рис.5.11,в, що має два зайві зв'язки,- двічі статично невизначеною.
Рішення статично невизначених завдань. Статично невизначені конструкції, елементи яких працюють на розтягання й стискання, будемо розраховувати, вирішуючи рівняння: