Разложение матриц в произведение простейших. Первый критерий обратимости

Пусть А ϵ M_mxn (|R). Будем говорить, что строка с номером I (столбец с номером j) приведена, если в этой строке (столбце) имеется элемент равный единице и при этом все остальные элементы столбца (строки), в котором расположен этот элемент, равны 0.

Назовем приведенной матрицу, у которой приведены все строки.

Назовем простейшей матрицу, у которой приведены все строки и столбцы.

Будем пользоваться понятиями элементарных преобразований матриц и понятием элементарных матриц.

ТЕОРЕМА:

Любая матрица при помощи преобразований, элементарных, строк и столбцов может быть приведена к простейшему виду.

ДОКОЗАТЕЛЬСТВО:

Теорема доказывается поэтапно.

A= 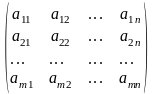, A≠0

1) Будем считать не ограничивая общности a₁₁≠0, т.к. в противном случае мы можем этого добиться изменением порядка следования строк и столбцов матрицы.

Разделим первую строку матрицы на 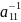= 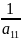, a₁₁≠0, в результате:

A=

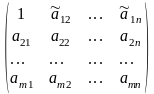
В результате продолжения элементарных преобразований получим матрицу с приведенной первой строкой.

2) Если все элементы, 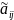=0, i>=2, то переходим к этапу m+1.

Если есть, ≠0, i>=2, то можем считать, что 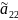≠0.

Выполняем преобразования аналогично 1) этапу, но с умножая каждую строку на 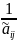и добиваясь того, чтобы во втором столбце все остальные элементы были нулями, мы получим матрицу с приведенной второй строкой.

Продолжая этот процесс не более чем после m шагов будет получена матрица вида:

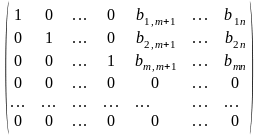
От столбца с номером m+ отнимем b_1,m+1 умноженное на первый столбец.

С^m+1-b_1,m+1*C¹

С^m+1-b_2,m+1*C²

С^m+1-b_m,m+1*C^m

И т.д. пока не кончатся все столбцы. В результате будет получено

СЛЕДСТВИЯ:

Dr=

Поскольку каждое элементарное преобразование строки равносильно умножению слева на соответствующую элементарную матрицу, а каждое элементарное преобразование столбца равносильно умножению на соответствующую матрицу справа, то по существу мы получим следующее равенство: E_s …E₁ E₂ A E¹ E²…E^p=Dr (1) => E_s …E₁=B^-1; E¹ E²…E^p=C^-1

ЛЕММА:

Каждая элементарная матрица обратима и обратная к ней есть элементарная матрица, соответствующая обратному элементарному преобразованию.

(С_i(↗↖)С_j)^-1=(C_j(↗↖)C_i)

Вернемся к равенству (1), Согласно лемме и свойству обратимости матриц, произведение элементарных матриц из равенства (1) есть обратимые матрицы:

В^-1АС^-1=Dr (2)

Умножая справа на С, а слева получим:

ВВ^-1АСС^-1=ВDrС, где ВВ^-1=En, СС^-1=En

В результате: А=ВDrC (3) разложение матрицы на простейшие

Предположим теперь, что в равенстве (3) матрица А является квадратной А ϵ M_mxn (|R).

Из предыдущего изложения видно, что в равенстве (3) все матрицы содержащиеся в правой части является квадратными и того же размера.

Поскольку по построению матрицы В и С обратимы, то введу равенства (3) обратимость матрицы А определяется обратимостью матрицы Dr.

Матрицы Dr в рассматриваемом случае имеет вид:

и (Еr)

ЛЕММА:

Матрица Dr обратима тогда и только тогда когда r=n

Доказательство:

Если r=n, то матрица Dr является единичной, а единичная матрица обратима.

Предположим, что r≠n, тогда r<n и матрица Dr имеет вид:

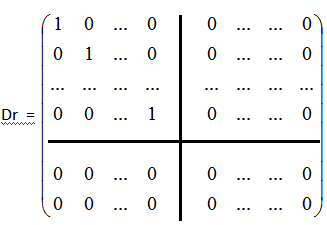
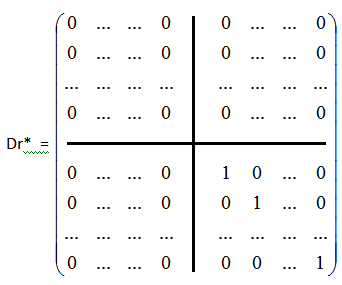
Нетрудно проверить, что Dr* Dr=0, Dr Dr*=0

Поэтому матрица Dr не может быть обратимой.