12. Гідравлічні втрати напору( загальні поняття). Еквівалентна довжина.
При русі рідини, в результаті дії сил в'язкого тертя, частина енергії витрачається на тертя до довжині потоку і в місцевих опорах (звуженнях, поворотах, розширеннях)
(8.1)
Втрати напору по довжині потоку пропорціональні його відносній довжині і швидкісному напорові (Дарсі, 1854 р.)
(8.2)
Втрати напору в місцевих опорах пропорціональні швидкісному напорові (Вейсбах. 1842 р )
(8.3)
В
формулі (8.2)
-
коефіцієнт
гідравлічного опору (тертя), залежить
від режиму руху рідини.
В
формулі (8.3)
-
коефіцієнт
місцевого опору. Величина
стала, якщо режим руху турбулентний.
При ламінарній течії
визначається за формулою
(8.4)
де С - коефіцієнт, який залежить від виду місцевого опору.
При розв'язанні задач формули (8 2) і (8.3) об'єднують в одну, формулу Дарсі-Вeйсбаха:
і
(8.5)
Тут
-
арифметична
сума значень коефіцієнтів місцевих
опорів. Так можна їх задавати, якщо
відстань між ними на
трубі більша 20
внутрішніх
діаметрів
Втрати
напору в місцевих опорах можна виразити
через еквівалентну
довжину
,
тобто
таку довжину трубопроводу,
при якій
,
(8.6)
Тоді
вираз (8.1)
для
запишеться
у вигляді
(8.7)
або, виразивши швидкість через витрату, одержимо
(8.8)
де
-
розрахункова
довжина трубопроводу
;
а- стала величина для даної конструкції трубопроводу.
При ламінарному режимі руху рідини коефіцієнт гідравлічного опору
(8.9)
і втрати напору на тертя обчисляються за формулою Пуазейля
(8.10)
При
турбулентному режимі руху (Re
>
)
розрізняють
три зони гідравлічного опору. В першій
зоні гідравлічно
"глад-ких"
труб
і
в межах
справедлива
формула Блазіуса
(811)
яка
використовується при Re
10
або
формула Конакова
(8.12)
де
-
еквівалентна
шорсткість.
В
другій зоні змішаного тертя
і
в межах
можна
використовувати формулу А. Альтшуля
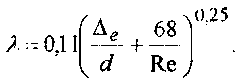(8.13)
В
третій зоні квадратичного опору або
гідравлічно шорстких
труб
і
при Re
>
найбільш
спрощеною
є
залежність Шифрінсона
(8.14)
Описані
вище величини
і
називають
першим і другим перехідними
числами
Рейнольдса.
13) Визначення втрат напору по довжині трубопроводу. Гідравлічний нахил
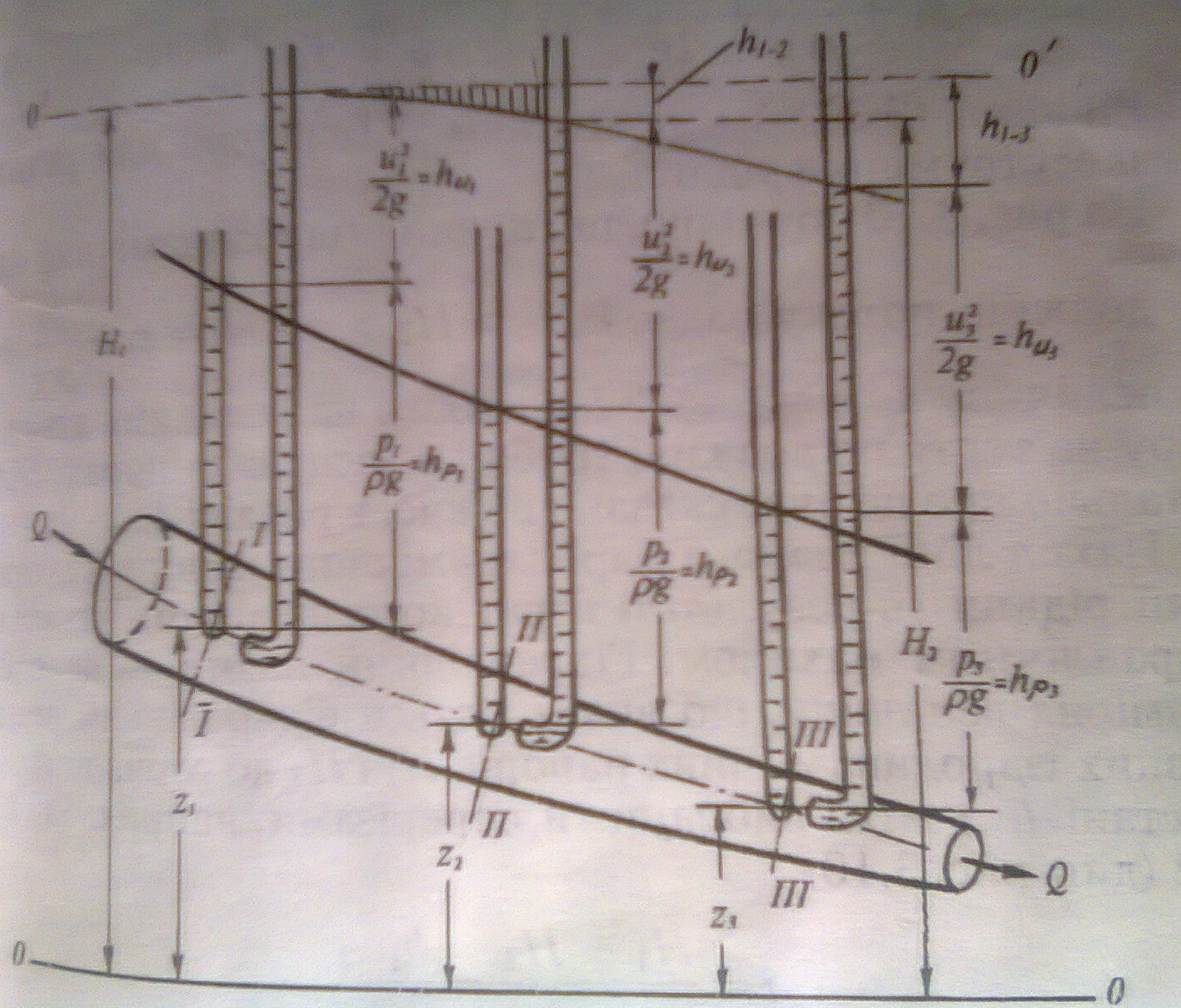
14. Визначення втрат напору на місцевих опорах. Втрати напору при раптовому розширенні.
15.Гідравлічний розрахунок трубопроводу.
Основні задачі:
Визначення початкового або кінцевого тиску, решта - відомо
Визначення витрати рідини , коли відомо: p1,p2,Re, шорсткість,коеф лін. опору
Підбір діаметра труби при відомих Q, p1,p2,Re
Підбір оптимального діаметра трубопроводу з точки зору мінімальних затрат на будівництво і експлуатаціюб решта – відомо.
Характеристика трубопроводу – це залежність необхідного напору від втрат рідини.
16.Гідравлічний розрахунок при паралельному і послідовному з`єднанні трубопроводів
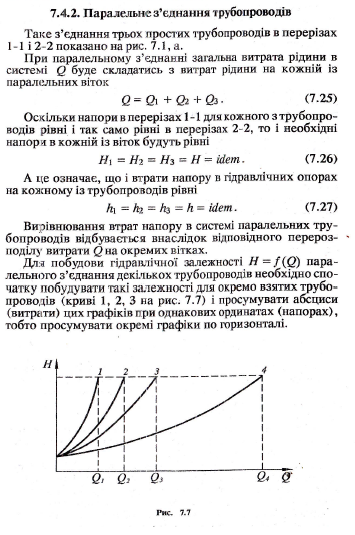
Крива 4 внаслідок такої побудови буде відображати залежності Н=f(Q) для всієї системи паралельних трубопроводів і може дати розв`язок для поставлених в гідравлічному розрахунку задач.