
- •1. Класифікація задач математичного програмування
- •2. Стохастичне програмування та його види
- •3. Загальна математична постановка задачі стохастичного програмування
- •4. Особливості математичної постановки задач стохастичного програмування
- •5. Методи розв’язування стохастичних задач
- •6. Одноетапні задачі стохастичного програмування
- •7. Двохетапні задачі стохастичного програмування
- •8. Приклади економічних задач стохастичного програмування
5. Методи розв’язування стохастичних задач
Методи розв’язування стохастичних задач поділяють на дві групи –
прямі та непрямі.
Прямі
методи використовують для розв’язування
задач стохастичного програмування,
коли існують способи побудови функцій
і
 на базі інформації щодо параметра ω.
на базі інформації щодо параметра ω.
Непрямими є методи зведення стохастичної задачі до задачі лінійного чи нелінійного програмування, тобто перехід до детермінованого аналога задачі стохастичного програмування.
Перший підхід застосовують тоді, коли в стабільній економічній ситуації розв’язки оптимізаційних задач навіть за різних зовнішніх впливів мало різняться між собою. Тоді оптимальні рішення приймаються на сонові відомих стохастичних характеристик розподілу випадкових параметрів умов задачі до спостереження за реалізаціями поточних значень цих параметрів. Прийняте таким способом рішення – найкраще середньостатистичне рішення, а відповідна задача називається одноетапною задачею стохастичного програмування. Однак у більшості випадків такий підхід може виявитися неприйнятним через значні коливання зовнішніх умов.
Частіше застосовують другій підхід, коли враховують випадковий характер цільової функції та функції обмежень. У цьому разі формально постановки задач стохастичного програмування мають певні відмінності; їх розрізняють за характером розв’язків, вибором показника якості рішення та способом розмежування обмежень задачі [3, c. 118].
Кожен з етапів розв’язку стохастичної задачі у свою чергу також може бути поділений. У такому разі маємо одноетапні чи двохетапні задачі стохастичного програмування.
Одноетапна задача стохастичного програмування використовується в тому разі, коли рішення приймаються на підставі відомих характеристик розподілу ймовірностей випадкових параметрів умови задачі до спостережень за їхніми реалізаціями. У такому разі має прийматися найкраще в середньостатистичному розумінні рішення. Тобто випадкові параметри задачі замінюють їх середніми величинами і початкову задачу стохастичного програмування зводять до детермінованої.
Двохетапна задача стохастичного програмування виникає тоді, коли процес прийняття рішення поділяють на два етапи.
На першому етапі вибирається попередній план, який задовольняє умови задачі за будь-якої реалізації випадкових параметрів. На другому етапі розраховується величина компенсації відхилень розробленого плану від фактичних значень, що були визначені після спостереження за реалізацією випадкових параметрів. Оптимальний план задачі визначають так, щоб забезпечити мінімум середнього значення загальних витрат, які виникають на обох етапах розв’язування задачі. Для існування розв’язку двохетапної задачі вибір плану на першому етапі має гарантувати існування плану-компенсації.
6. Одноетапні задачі стохастичного програмування
Розглянемо лінійну одноетапну задачу стохастичного програмування в такій постановці: визначити план Х, для якого
 ,
,
 ,
,

 ,
,
де
вектор коефіцієнтів при змінних у
цільовій функції
 ,
матриця коефіцієнтів при змінних у
системі обмежень
,
матриця коефіцієнтів при змінних у
системі обмежень

 ,
а також вектор
,
а також вектор

 є
випадковими величинами; ω — випадковий
параметр, Ω — множина значень ω, що
з’являються з певною ймовірністю. Нехай
є
випадковими величинами; ω — випадковий
параметр, Ω — множина значень ω, що
з’являються з певною ймовірністю. Нехай
 — нормально розподілена випадкова
величина з математичним сподіванням
— нормально розподілена випадкова
величина з математичним сподіванням
 і дисперсією
і дисперсією
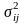 ,
а
,
а
 і
і
 — нормально розподілені випадкові
величини з математичними сподіваннями
відповідно
— нормально розподілені випадкові
величини з математичними сподіваннями
відповідно
 та
та
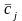 і дисперсіями
і дисперсіями
 .
.
Оскільки
в обмеженнях задачі виду
 матриця
та вектор
є нормально розподіленими випадковими
величинами, то їх різниці
матриця
та вектор
є нормально розподіленими випадковими
величинами, то їх різниці

 також
є випадковими величинами з нормальним
розподілом, математичним сподіванням
також
є випадковими величинами з нормальним
розподілом, математичним сподіванням
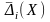
 і дисперсією
і дисперсією
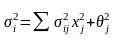 .
.
Обмеження
еквівалентні нерівностям
 .
Враховуючи, що
.
Враховуючи, що
 нормально розподілена випадкова
величина, використаємо функцію нормального
закону розподілу, внаслідок чого наведену
нерівність можна записати так:
нормально розподілена випадкова
величина, використаємо функцію нормального
закону розподілу, внаслідок чого наведену
нерівність можна записати так:
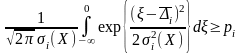
 .
.
Позначимо:
 .
Тоді останню нерівність зведемо до
вигляду:
.
Тоді останню нерівність зведемо до
вигляду: ,
звідки
,
звідки
 .
.
Підставивши
в цю нерівність значення
 і
і
 ,
отримаємо:
,
отримаємо:
 .
.
Отже, початкову стохастичну задачу зведено до детермінованого аналогу з лінійною цільовою функцією та нелінійними обмеженнями:
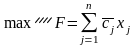 за
умов:
.
за
умов:
.
Таку задачу можна розв’язати одним з відомих методів розв’язування задач нелінійного програмування, наприклад, методом множників Лагранжа [2, c.406].
