2. Механическая работа

Если действующая на тело сила F вызывает его перемещение s, то действие этой силы характеризуется величиной, называемой механической работой .

Механической работой А называют скалярную величину, равную произведению модуля силы F, действующей на тело, и модуля перемещения s, совершаемого телом в направлении действия этой силы, т. е.

А=Fs.    (3.9)

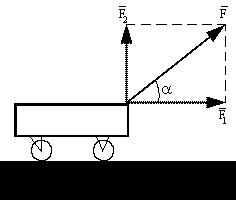
В случае, описываемом формулой (3.9), направление перемещения тела совпадает с направлением силы. Однако чаще встречаются случаи, когда сила и перемещение составляют между собой угол, не равный нулю или p. (рис. 30)

Разложим силу F на две взаимно перпендикулярные составляющие F₁ и F₂ (F=F₁+F₂). Поскольку механическая работа - величина скалярная, то работа силы F равна алгебраической сумме работ сил F₁ и F₂, т. е. А=А₁+А₂.

Под действием силы F₂ тело перемещения не совершает, так как F₂^s. Поэтому A₂=0. Следовательно, работа А=А₁=F₁s. Из рисунка видно, что F₁=Fcosa. Поэтому

А=Fsсоsa.    (3.10)

Таким образом, в общем случае механическая работа равна произведению модуля силы и модуля перемещения на косинус угла между направлениями силы и перемещения. Работа силы, направленной вдоль перемещения тела, положительна, а силы, направленной против перемещения тела, - отрицательна. По формулам (3.9) и (3.10) вычисляют работу постоянной силы. Единицу механической работы устанавливают из формулы (3.9). В СИ за единицу работы принята работа силы 1 Н при перемещении точки ее приложения на 1 м. Эта единица имеет наименование джоуль (Дж):  1 Дж = 1Н·1м.

Работа силы тяжести

Вычислим работу силы тяжести. Для этого воспользуемся формулой:

(1) A = FScosα

Пусть тело движется вертикально. При небольших расстояниях от поверхности Земли сила тяжести постоянна и по модулю равна mg. Рассмотрим простейший случай - свободное падение тела. Выберем некоторый уровень, относительно которого будем рассматривать падение тела. Высоту выбранного уровня примем равной нулю. Такой уровень называют нулевым (В качестве нулевого уровня может быть уровень моря, поверхность Земли, дно ямы, вырытой в земле, пол класса и т. д.) Пусть тело массой m свободно падает с высоты h₁ над нулевым уровнем, до высоты h₂ над тем же уровнем (Рис.1).

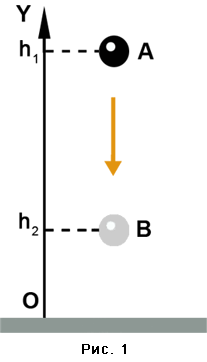
При этом перемещение тела по модулю равно h₁ - h₂. Так как направления перемещения и силы совпадают, то работа силы тяжести равна

(2) A = mg(h₁ - h₂)

Если тело падает с некоторой высоты h до нулевого уровня, то работа силы тяжести выражается равенством

(3) A = mgh

Если тело брошено вверх с нулевого уровня и поднимается на высоту h над ним, то работа силы тяжести отрицательна и равна

(4) A = - mgh

Теперь выясним, какую работу совершает сила тяжести в случае, когда тело движется не по вертикали.

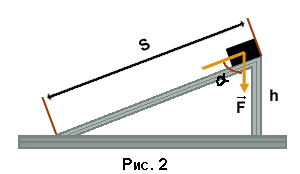
В качестве примера рассмотрим движение тела по наклонной плоскости. Пусть тело массой m совершает перемещение s, по модулю равное длине наклонной плоскости, высотой h. Работа силы тяжести в этом случае равнаA = FScosα, где α - угол между векторами силы и перемещения.

Заметим, что Scosα = h. Поэтому A = mgh.

Мы получили для работы силы тяжести то же выражение, что и в случае движения по вертикали. Значит, работа силы тяжести не зависит от того, движется ли тело по вертикали или проходит более длинный путь по наклонной плоскости.

Заметим, что любую произвольную траекторию движения тела можно свести к движению по маленьким наклонным плоскостям. В результате работа силы тяжести определяется "потерей высоты" (или набором высоты) не только при движении по наклонной плоскости, но и по любой другой траектории.

Таким образом, работа силы тяжести не зависит от формы траектории движения тела и всегда равна произведению модуля силы тяжести на разность высот в исходном и конечном положениях.

При движении вниз работа положительна, при движении вверх - отрицательна. Работа силы тяжести (также как и работа силы упругости)на замкнутой траектории равна нулю.

Работа силы упругости

Сила упругости - это сила, возникающая при деформации тела.

Для удобства рассмотрим силу упругости, возникающую в деформированной пружине (заметим, что все закономерности, установленные для пружины, относятся и к другим деформированным телам). Будем считать, что деформация является упругой. Тогда согласно закону Гука сила упругости пропорциональна деформации, т. е. удлинению пружины. Направлена сила в сторону, противоположную смещению частиц тела при деформации.

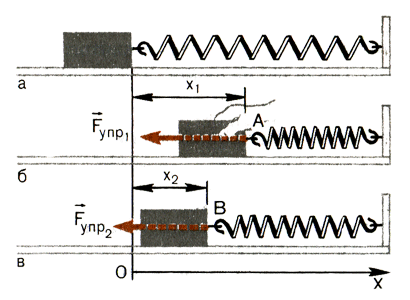
На рисунке а показана пружина в недеформированном состоянии. Правый конец пружины закреплен, а к левому прикреплено некоторое тело. Направим ось координат X так, как показано на рисунке. Сожмем пружину, сместив ее левый конец вправо на расстояние x₁. В результате деформации возникает сила упругости (рис. б), направленная влево. Проекция этой силы на ось X равна - kx₁, где k - жесткость пружины.

Предоставим теперь пружину самой себе. Тогда конец пружины будет смещаться влево. При этом движении сила упругости совершает работу.

Предположим, что левый конец пружины (и тело, скрепленное с ним) переместился из положения А в положение В (рис. в). В этом положении деформация (удлинение) пружины равна x₂ , а проекция этой силы на ось X равна - kx₂. Перемещение конца пружины равно разности координат конца пружины: x₁ - x₂.

Направления силы и перемещения совпадают, и чтобы найти работу, нужно перемножить модули силы упругости и перемещения. Но сила упругости при движении изменяется от точки к точке, т. к. изменяется удлинение пружины. Для вычисления работы силы упругости используем среднее значение силы упругости. Среднее значение силы упругости равно полусумме начального и конечного ее значений:

(1)

Тогда

(2) A = F_ср(x₁ - x₂)

(3)

Вспомним, что (x₁ - x₂)(x₁ + x₂) = x₁² - x₂². Тогда

(4)

Как видно из формулы (4), работа зависит только от координат x₁ и x₂начального и конечного положений конца пружины (x₁ и x₂ - это и удлинения пружины, и координаты ее конца).

Поэтому работа силы упругости (также как и работа силы тяжести) не зависит от формы траектории. На замкнутой траектории работа силы упругости равна нулю.

Работа силы трения

Реальное движение всегда происходит в среде и встречается с силой ее сопротивления и трения. Если мы толкнем любое тело, то оно быстро остановится. Движение его описывает равнодействующая сил- вертикальная сила тяжести, перпендикулярная поверхности реакция опоры, и сила трения вдоль нее. Силы реакции перпендикулярны направлению перемещения и компенсирует силу тяжести на горизонтали и не совершают работы. Поэтому работу определяет сила трения, направленная против движения

Результирующая силаF_р = mg+N+F_тр=F_тр. По теореме об изменении кинетической энергии оно равно работе равнодействующей силы – трения, А_р=Е_к2-Е_к1=0-½mv²=A_тр<0.

 При трении частицы тел деформируются, колеблются и нагреваются, как можно заметить (так извлекали звук и огонь). Температура тел определяется средней кинетической энергией молекул тела и нагревание означает ее увеличение, за счет кинетической энергии тела в целом. Та из механической направленной превращается в хаотичную, тепловую, внутреннюю.

 По закону сухого трения F_тр=μN,A=F_трscosα=-μNs.

Эта работа зависит от путиs, проходимого телом. При замкнутому пути, возвращении в исходное место, работа силы трения не равна нулю. Сила трения не является потенциальной, не имеет потенциальной энергии.

Такие силы, работа которых зависит от формы траектории движения, называются не потенциальными и диссипативными (dissipative- рассеяние).

Сила сопротивления среды направлена против движения тел и совершает отрицательную работу.

Но именно благодаря этой силе можно двигаться по земле. При ходьбе ноги или колеса отталкивается от земли (назад) и движутся вперед силой реакции и трения покоя (противодействия по 3 закону Ньютона), направленной по движению и выполняющей положительную работу.

Тела на/в движущихся средствах транспорта также приобретают скорость благодаря силе трения.

 

Сила трения скольжения зависит от скорости, при меньших скоростях пропорционально (F_c=kv), при больших пропорционально квадрату скорости (F=kv²,см.гидродинамику)