2. По табл. 3.2 вычисляются индексы критериев.

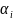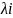Пусть - среднее значение, взятое по всем элементам i-го столбца (кроме единицы). Тогда (индекс i-го критерия) вы­числяется из соотношений:

Индекс критериев может быть назван коэффициентом вни­мания, которое следует уделять критерию при поиске решения.

Предположим, что все элементы i-го столбца в табл. 3.2 близки к единице. Тогда среднее значение тоже близко к еди­нице, (1 — ) мало и соответствующий индекс мал. Действи­тельно, если при оптимизации по другим критериям значение данного критерия близко к наилучшему, то ему вряд ли стоит уделять внимание. Наоборот, критерию, сильно зависящему от изменений других критериев ( мало), должны соответствовать большие значения индекса. Индексы называют иногда техни­ческими весами потому, что в отличие от весов wi они не на­значаются ЛПР, а вычисляются.

3. Производится оптимизация по глобальному критерию. Глобальный критерий имеет вид

где определяются из (3).

Решение, найденное при оптимизации, предъявляется ЛПР.

Фаза анализа

1. ЛПР анализирует вектор значений критериев y1, най­денный при оптимизации по критерию (4). Затем ему задается вопрос: все ли компоненты вектора y1 имеют удовлетворитель­ные значения? Если да, то решение получено. Если нет, то ЛПР указывает один критерий с наименее удовлетворительным значением.

2. ЛПР просят назначить для критерия с наименее удовле­творительным значением пороговое значение l_i, при достиже­нии которого можно признать этот критерий имеющим удовле­творительное значение:

Условие (5) добавляется к совокупности линейных равенств и неравенств, определяющих область В допустимых значений переменных. Таким образом, возникает уже новая область до­пустимых значений.

На этом фаза анализа заканчивается. Следующий шаг на­чинается с фазы расчетов при новой области допустимых зна­чений и т.д. При достижении удовлетворительных для ЛПР значений по всем критериям ЧМП останавливается.

7. Пример применения метода SТЕМ: как управлять персоналом

Французской консультативной фирмой SSSS предложена модель, характеризующая изменения со временем состава пер­сонала большой организации и продуктивности ее работы. Модель применялась для прогнозирования последствий раз­личных вариантов управления кадрами организации. Проверя­лись разные стратегии приема на работу и повышения в долж­ности через два, три и четыре года. В качестве переменных мо­дели рассматривалось количество сотрудников, назначенных на различные должности в определенные периоды времени.

Использовались четыре критерия, представляющих собой линейные функции от переменных: общее «удовлетворение» кадров (SA); фактическая эффективность работы кадров (EF); стоимость приема на работу дополнительных сотрудников (ЕВ); стоимость нехватки кадров по отношению к прогнозируемым потребностям (ЕС).

В модель были заложены следующие зависимости:

• эффективность работы сотрудника линейно зависит от отно­шения оценки его возможностей Q к оценке требований t, предъявляемых должностью к сотруднику;

• удовлетворение сотрудника во время пребывания на опреде­ленной должности сначала возрастает до максимального зна­чения, а затем со временем уменьшается до первоначального значения также в зависимости от отношения Q к t.

С математической точки зрения проблема представляла со­бой задачу линейного программирования с четырьмя крите­риями качества, 350 переменными и 200 ограничениями. Не имелось никакой априорной информации о сравнительной важности критериев.

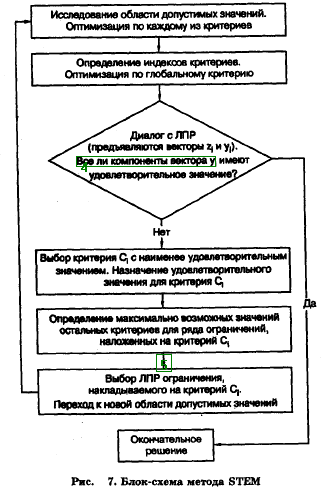
Для решения был использован метод STEM]. На первом этапе решения в области допустимых значений была осуществ­лена оптимизация по каждому из критериев. Затем при помощи линейного преобразования истинных значений критериев к зна­чениям в интервале (0,1) (нормирования) был выполнен переход к относительным значениям критериев. Значения критериев при поочередной оптимизации по каждому из них приведены в табл. 3.3. Данные таблицы говорят о сильной зависимости критериев SA и EF и о противоречивости этих критериев и критериев ЕВ и ЕС; последние два противоречивы также друг другу.

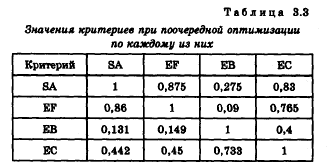
Далее на основе приведенной таблицы были определены на­чальные индексы (технические веса) критериев. Пусть (a_ср)_v -среднее по v-му столбцу значение всех элементов, кроме мак­симального (равного 1). Определим

Индексы критериев находим из условия

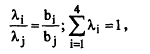
Такой способ определения технических весов отражает стремление найти в области допустимых решений вершину с наилучшими значениями по всем критериям.

Затем проводилась оптимизация по глобальному критерию, что дало следующий результат:

Для диалога с ЛПР значения по критериям ЕВ и ЕС были представлены в единицах стоимости. ЛПР предъявлялись: век­тор z1 максимальных значений, достигаемых при максимиза­ции по каждому из критериев по отдельности, и вектор y1 зна­чений критериев, достигаемых при оптимизации по глобально­му критерию с приведенными выше индексами:

Перед ЛПР был поставлен вопрос: все ли компоненты век­тора y1 имеют удовлетворительные значения? При ответе на этот вопрос использовался вектор z1, компоненты которого представляли собой максимально возможные (недостижимые одновременно) значения компонентов вектора y1. Руководитель определил значение по критерию ЕВ как наименее удовлетво­рительное и нашел нижний уровень по критерию ЕВ: -1000.

Далее были найдены максимально возможные значения трех прочих критериев при ряде ограничений, дополнительно накладываемых на критерии ЕВ:

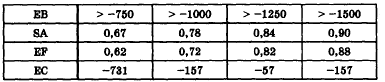
При рассмотрении этой таблицы руководитель выбрал век­тор при ЕВ > —1500 как обеспечивающий приемлемый ком­промисс между повышением качества по критерию ЕВ и пони­жением качества по критериям SA и ЕF. Для новой области допустимых решений (при ЕВ > —1500) приведенным выше способом были подсчитаны новые значения индексов для трех критериев:

Далее была проведена оптимизация по глобальному крите­рию с индексами. Полученное решение (вектор У2) вместе с вектором z2 максимальных значений критериев, достигаемых уже при новой области допустимых значений переменных, было предъявлено

ЛПР во время третьего диалога с ним. Руко­водитель определил значение по критерию ЕС как наименее удовлетворительное и выбрал в качестве нижнего уровня по ЕС значение -600.

Затем были определены максимально возможные значения двух критериев при ряде ограничений, накладываемых на ЕС:

Руководитель выбрал вектор при ЕС > —800 как обеспечи­вающий приемлемый компромисс между повышением качества по критерию ЕС и понижением качества по критериям SА и ЕF. Зная сильную взаимозависимость критериев SА и ЕF, он выбрал решение, соответствующее максимуму ЕF, как оконча­тельное решение проблемы: