
- •Задача 5. МногоФакторный эксперимент а. Многофакторное уравнение регрессии первого порядка
- •5.3. Проверка многофакторного уравнения регрессии первого порядка на адекватность.
- •Б. Многофакторное уравнение регрессии второго порядка
- •Типовая задача (уравнение регрессии первого порядка)
- •3.2. Выполним предварительную обработку экспериментальных данных (внести в таблицу 3).
- •4. Создадим матрицу моделирования для построения двухфакторного уравнения регрессии первого порядка на базе цпфп (таблица 4) (раздел а, п. 5).
- •4.3. Проверим полученное двухфакторное уравнение регрессии первого порядка на адекватность по критерию Фишера (результаты расчета внесем в таблицу 4):
- •План решения типовой задачи (уравнение регрессии второго порядка)
- •Решение задачи по плану
- •2.4. Проверим полученное ортогонализированное двухфакторное уравнение регрессии второго порядка на адекватность по критерию Фишера:
- •Формулировки 30 вариантов контрольных задач
5.3. Проверка многофакторного уравнения регрессии первого порядка на адекватность.
Дисперсия
адекватности
![]() и её число степеней свободы
и её число степеней свободы
![]() равны:
равны:
![]() , (24)
, (24)
![]() , (25)
, (25)
где
n – число
дублей в каждом опыте;
![]() ‑ остаточная
сумма квадратов;
‑ остаточная
сумма квадратов;
![]() ‑ расчетные
значения параметра Y,
полученные по многофакторному
уравнению регрессии первого
порядка
‑ расчетные
значения параметра Y,
полученные по многофакторному
уравнению регрессии первого
порядка
![]() (
),
которое содержит только значимые
коэффициенты;
Nk ‑ число
опытов; В ‑ число
значимых коэффициентов многофакторного
уравнения регрессии первого
порядка.
(
),
которое содержит только значимые
коэффициенты;
Nk ‑ число
опытов; В ‑ число
значимых коэффициентов многофакторного
уравнения регрессии первого
порядка.
Адекватность уравнения регрессии проверяется по критерию Фишера:
‑ экспериментальное значение критерия Фишера Fэ, (отношение большей дисперсии к меньшей):
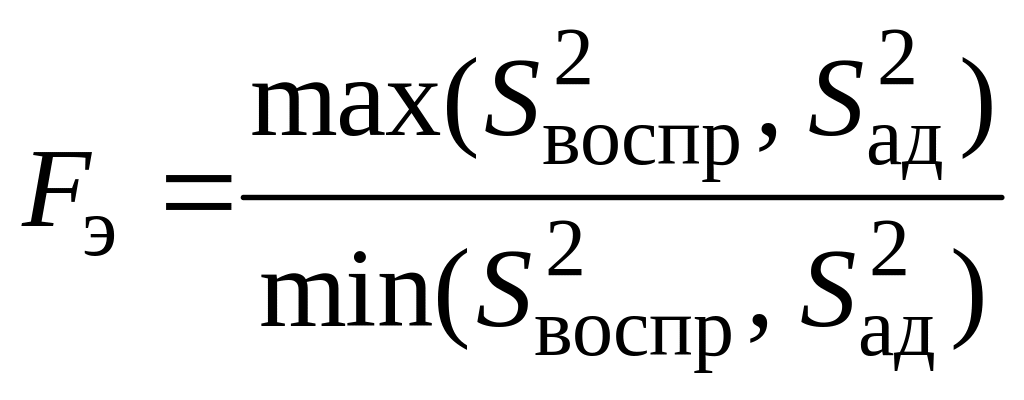 , (26)
, (26)
‑ табличное
значение критерия Фишера
![]() ,
где
,
где
![]() ‑ число
степеней свободы большей
дисперсии,
‑ число
степеней свободы большей
дисперсии,
![]() ‑ число
степеней свободы меньшей
дисперсии, выбирается из таблицы
Приложения 4;
‑ число
степеней свободы меньшей
дисперсии, выбирается из таблицы
Приложения 4;
‑ уравнение регрессии с доверительной вероятностью р адекватно, если:
![]() , (27)
, (27)
‑ уравнение регрессии с доверительной вероятностью р неадекватно, если:
![]() . (28)
. (28)
6.
Абсолютная погрешность
![]() параметра
параметра
![]() рассчитанного по уравнению
рассчитанного по уравнению
![]() ,
в случае его адекватности, определяется
по формуле:
,
в случае его адекватности, определяется
по формуле:
![]() , (29)
, (29)
где ‑ табличное значение критерия Стьюдента при числе степеней свободы и доверительной вероятности р находится из таблицы Приложения 2.
7. Если полученное многофакторное уравнение регрессии первого порядка неадекватно, следует перейти к построению многофакторного уравнению регрессии второго порядка.
Б. Многофакторное уравнение регрессии второго порядка
8.
Квадратичная
модель: многофакторное
ортогонализированное
уравнение регрессии второго
порядка, выражающее зависимость параметра
Y
от k
факторов
![]() ,
имеет следующий вид:
,
имеет следующий вид:
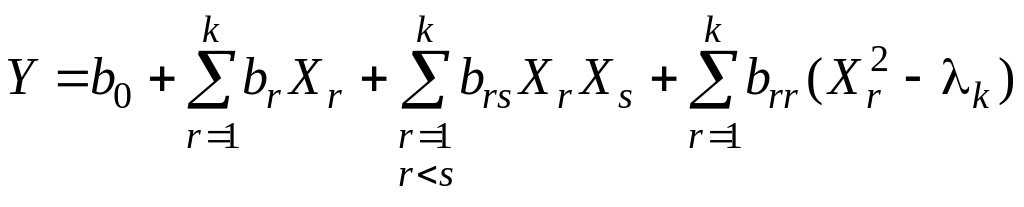 . (30)
. (30)
9.
Матрица
планирования для
построения многофакторного
уравнения регрессии второго
порядка представляет собой таблицу,
состоящую из
опытов с числом дублей n
каждый, включает в себя столбцы: Nk,
,
![]() ,
,
,
,
значения которых позволяют выполнить
предварительную обработку экспериментальных
данных (расчёт выборочных средних и
выборочных дисперсий в каждом опыте,
проверка выборочных дисперсий на
однородность, расчёт дисперсии
воспроизводимости). Такая матрица
создаётся
на базе ортогонального центрального
композиционного плана (ОЦКП), который
включает опыты ЦПФП и дополнительные
опыты в звёздных точках – по 2
опыта на каждый фактор
,
,
,
,
значения которых позволяют выполнить
предварительную обработку экспериментальных
данных (расчёт выборочных средних и
выборочных дисперсий в каждом опыте,
проверка выборочных дисперсий на
однородность, расчёт дисперсии
воспроизводимости). Такая матрица
создаётся
на базе ортогонального центрального
композиционного плана (ОЦКП), который
включает опыты ЦПФП и дополнительные
опыты в звёздных точках – по 2
опыта на каждый фактор
![]() ,
,
![]() .
Количество опытов ОЦКП при числе факторов
равно
.
Количество опытов ОЦКП при числе факторов
равно
![]() .
Величина звездного плеча
.
Величина звездного плеча
![]() для ОЦКП рассчитывают по формуле:
для ОЦКП рассчитывают по формуле:
![]() , (31)
, (31)
10. Так как число
опытов по сравнению с ранее проведенным
экспериментом для построения
многофакторного
уравнения регрессии первого
порядка увеличилось на
![]() опытов (звёздные точки), то необходимо
заново провести предварительную
обработку экспериментальных данных в
каждом опыте
с числом дублей n
каждый по уравнениям (6) – (12).
опытов (звёздные точки), то необходимо
заново провести предварительную
обработку экспериментальных данных в
каждом опыте
с числом дублей n
каждый по уравнениям (6) – (12).
11. Матрица
моделирования
для построения многофакторного
ортогонализированного
уравнения регрессии второго
порядка строится на базе ОЦКП
из
![]() опытов и включает в себя столбцы:
,
опытов и включает в себя столбцы:
,
![]() ,
,
![]() ,
,
,
,
,
,
![]() ,
,
![]() ,
,
![]() ,
,
значения которых позволяют провести
окончательную обработку экспериментальных
данных (расчёт коэффициентов уравнения
регрессии
,
,
значения которых позволяют провести
окончательную обработку экспериментальных
данных (расчёт коэффициентов уравнения
регрессии
![]() и проверка их на значимость, проверка
уравнения регрессии на адекватность,
расчёт абсолютной погрешности и
оптимизация в случае адекватности
уравнения регрессии). Ортогонализирующий
коэффициент для квадратичного фактора
рассчитывают по уравнению:
и проверка их на значимость, проверка
уравнения регрессии на адекватность,
расчёт абсолютной погрешности и
оптимизация в случае адекватности
уравнения регрессии). Ортогонализирующий
коэффициент для квадратичного фактора
рассчитывают по уравнению:
![]() . (32)
. (32)
12. Коэффициенты многофакторного ортогонализированного уравнения регрессии второго порядка рассчитывают по формулам:
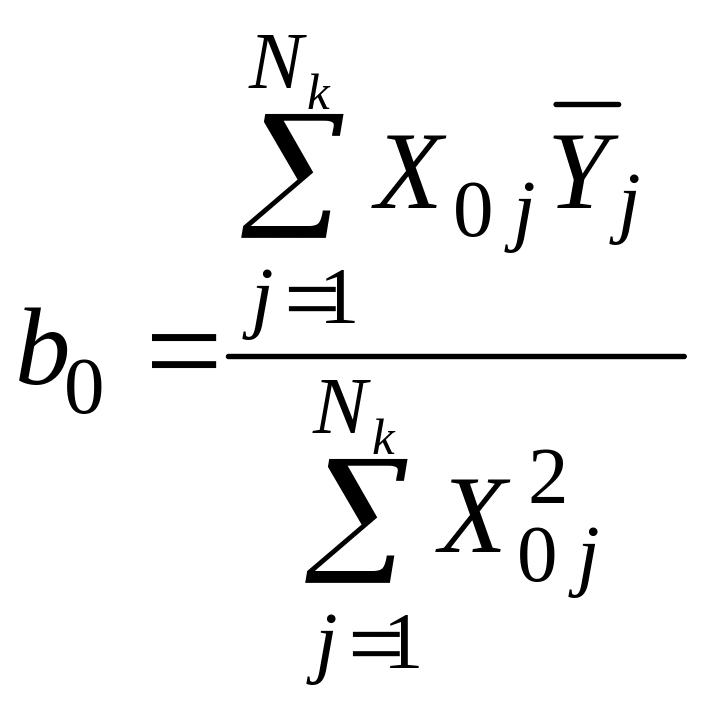 , (33)
, (33)
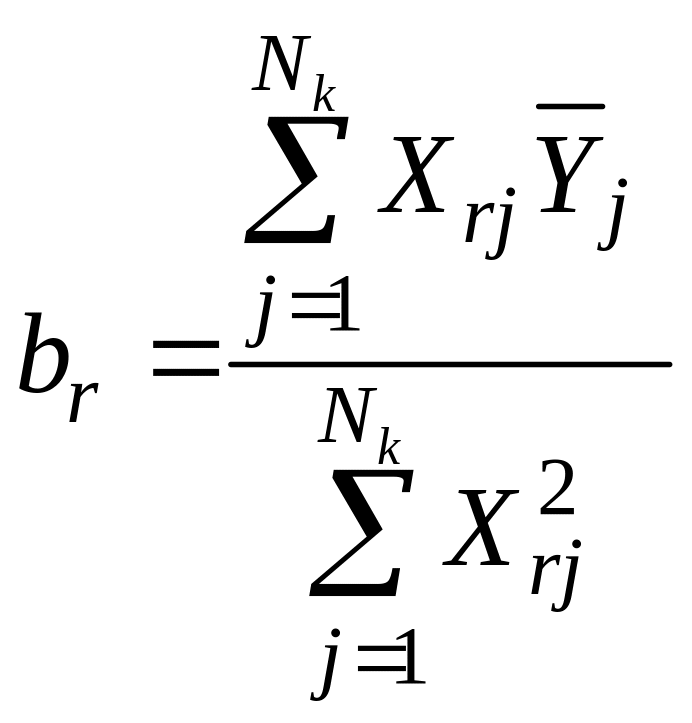 ,
, (34)
,
, (34)
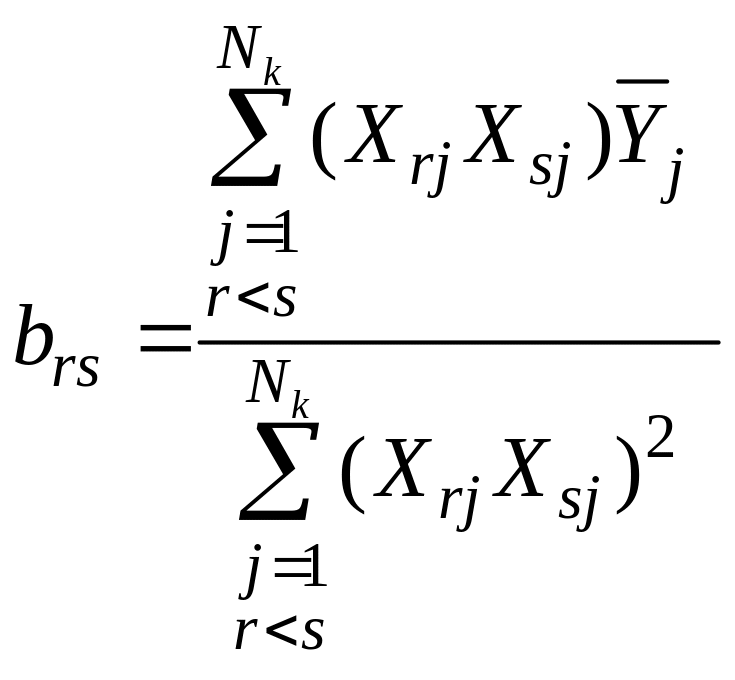 ,
,
![]() , (35)
, (35)
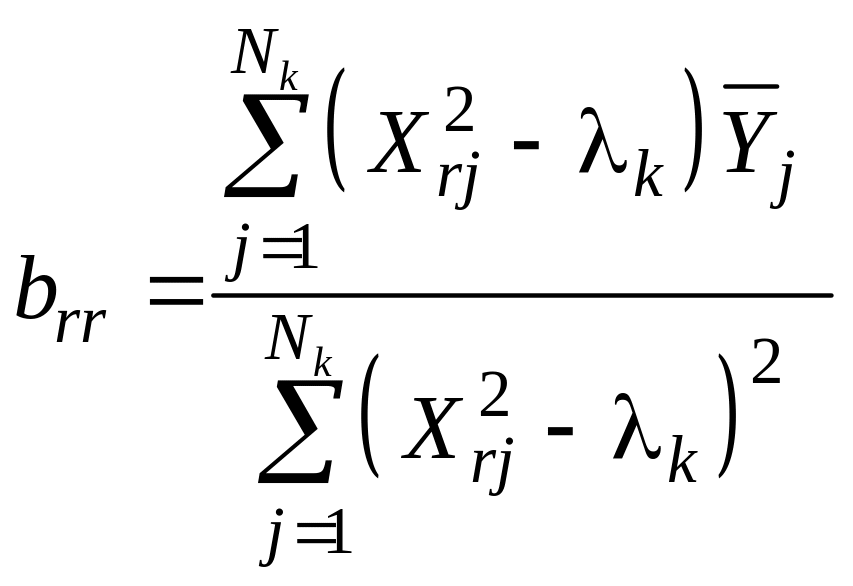 ,
. (36)
,
. (36)
13. Дисперсии значимости коэффициентов многофакторного ортогонализированного уравнения регрессии второго порядка рассчитывают по формулам:
, (37)
, , (38)
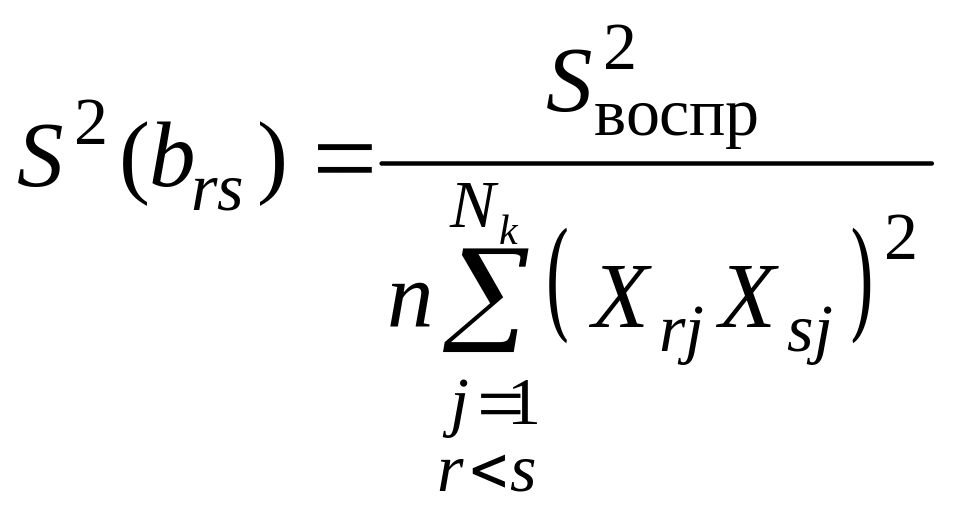 ,
, (39)
,
, (39)
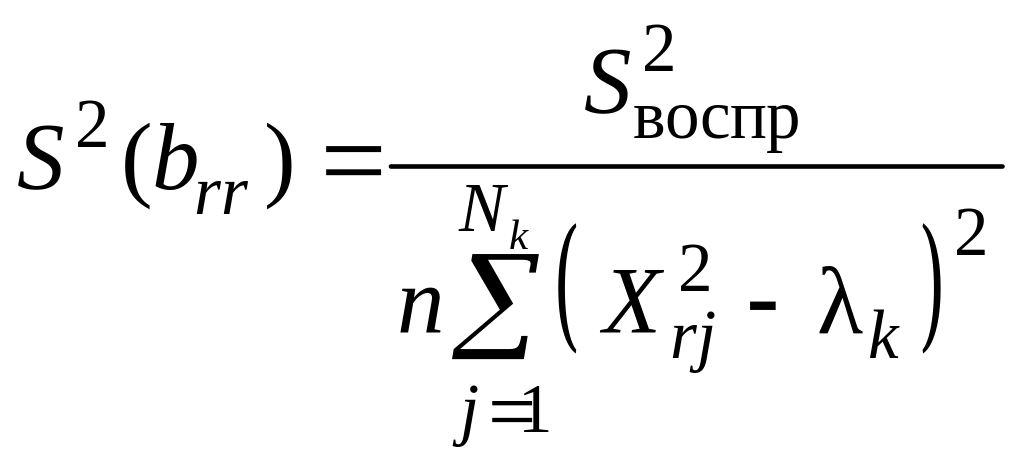 ,
. (40)
,
. (40)
Отметим свойство матрицы моделирования на базе ОЦКП (см. уравнения (38) – (40):
, , (41)
![]() ,
,
![]() . (42)
. (42)
![]() ,
. (43)
,
. (43)
14. Доверительные интервалы коэффициентов многофакторного ортогонализированного уравнения регрессии второго порядка рассчитывают по формулам:
![]() , (44)
, (44)
![]() ,
, (45)
,
, (45)
![]() ,
, (46)
,
, (46)
![]() ,
, (47)
,
, (47)
где
![]() ‑ критическое
значение критерия Стьюдента при числе
степеней свободы
‑ критическое
значение критерия Стьюдента при числе
степеней свободы
![]() и доверительной вероятности р
находится
из таблицы Приложения 2.
и доверительной вероятности р
находится
из таблицы Приложения 2.
Из равенства дисперсий (41) – (43) следует равенство доверительных интервалов:
, , (48)
![]() ,
, (49)
,
, (49)
![]() ,
. (50)
,
. (50)
15. Коэффициенты уравнения регрессии второго порядка значимы, если:
![]() , (51)
, (51)
![]() ,
, (52)
,
, (52)
![]() ,
, (53)
,
, (53)
![]() ,
,
. (54)
,
,
. (54)
Если для какого-либо регрессионного коэффициента указанное неравенство не выполняется, то этот регрессионный коэффициент незначим, и он исключается из полученного уравнения регрессии.
16. Дисперсия
адекватности
![]() и её число степеней свободы для
многофакторного
ортогонализированного
уравнения регрессии второго
порядка рассчитывают по формуле:
и её число степеней свободы для
многофакторного
ортогонализированного
уравнения регрессии второго
порядка рассчитывают по формуле:
, (55)
, (56)
где n – число дублей в каждом опыте; ‑ остаточная сумма квадратов; ‑ значение параметра Y, рассчитанное по многофакторному ортогонализированному уравнению регрессии второго порядка , в котором оставлены только значимые коэффициенты, ‑ число опытов; В – число значимых коэффициентов многофакторного уравнения регрессии второго порядка.
17. Адекватность уравнения регрессии любого порядка проверяется по критерию Фишера (см. уравнения (26) – (28)).
18. Предельную
абсолютную погрешность
![]() параметра
параметра
![]() рассчитанного по двухфакторному
ортогонализированному
уравнению регрессии второго
порядка
,
определяют по формуле:
рассчитанного по двухфакторному
ортогонализированному
уравнению регрессии второго
порядка
,
определяют по формуле:
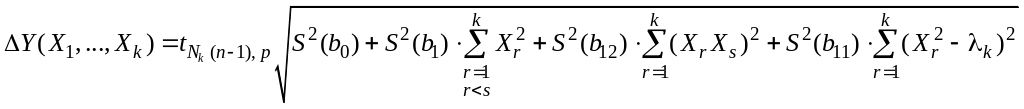 ,
(57)
,
(57)
где ‑ критическое значение критерия Стьюдента при числе степеней свободы и доверительной вероятности р находится из таблицы Приложения 2.
19. Если многофакторное
ортогонализированное
уравнение регрессии второго
порядка
адекватно и все регрессионные коэффициенты
![]() отрицательные (положительные), то
уравнение регрессии имеет абсолютный
максимум (минимум)
отрицательные (положительные), то
уравнение регрессии имеет абсолютный
максимум (минимум)
![]() .
Если к тому же все коэффициенты
незначимы, то:
.
Если к тому же все коэффициенты
незначимы, то:
![]() ,
. (58)
,
. (58)
