ОБЩИЕ МЕТОДИЧЕСКИЕ УКАЗАНИЯ
РАБОЧАЯ ПРОГРАММА
ЛИТЕРАТУРА
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ
ЗАДАЧИ КОНТРОЛЬНОЙ РАБОТЫ
Порядок выбора варианта задания
В контрольную работу входит четыре задачи. Вариант задания выбирается по первой букве фамилии и последней цифре шифра зачетной книжки. По первой букве фамилии студента определяются номера задач согласно таблице вариантов задания (таб. 5.1), а по последней цифре шифра выбираются числовые значения величин в задачах. Например, студент Борисов, имеющий зачетную книжку 1505458, решает задачи1.2; 2.2; 3.2; 4.2 по варианту 8 таблицы числовых значений величин (табл. 5.2).
Таблица 5.1 – Таблица вариантов заданий
Первые буквы фамилий |
Номера задач |
А, Е, Ё, Л, Р, Х, Э |
1.1, 2.1, 3.1, 4.1, 5.1 |
Б, Ж, М, С, Ц |
1.2, 2.2, 3.2, 4.2, 5.2 |
В, З, Н, Т, И, Я |
1.3, 2.3, 3.3, 4.3, 5.3 |
Г, Й, О, Ч, Ш |
1.4, 2.4, 3.4, 4.4, 5.4 |
Д, К, П, Ф, Щ |
1.5, 2.5, 3.5, 4.5, 5.5 |
Задача 1.1 … 1.5
 Плавающий
автомобиль, который в упрощенном
представлении можно считать прямоугольным
понтоном, имеет длину L
и
ширину B.
Автомобиль без груза имеет осадку в
пресной воде, равную
H0.
Определить массу груза и остойчивость
автомобиля в нагруженном состоянии,
если осадка его при этом равна
H,
а высота центра тяжести над дном
h.
(рис. 5.1).
Плавающий
автомобиль, который в упрощенном
представлении можно считать прямоугольным
понтоном, имеет длину L
и
ширину B.
Автомобиль без груза имеет осадку в
пресной воде, равную
H0.
Определить массу груза и остойчивость
автомобиля в нагруженном состоянии,
если осадка его при этом равна
H,
а высота центра тяжести над дном
h.
(рис. 5.1).
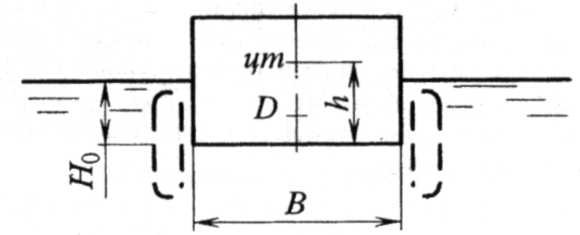
Рисунок 5.1
Цилиндрический резервуар заполнен жидкостью Ж до высоты 0.8 H. Диаметр резервуара D, температура жидкости 20
 .
Определить:
.
Определить:
объем жидкости, слившийся из резервуара при его вращении с частотой
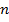 вокруг его вертикальной оси;
вокруг его вертикальной оси;
силу давления на дно резервуара и горизонтальную силу, разрывающую резервуар по сечению 1-1 при его вращении (рис. 5.2.).
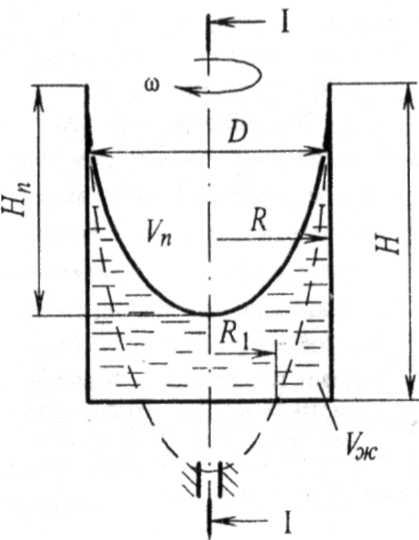
Рисунок 5.2
Указание.
При
вращении жидкости вместе с цилиндрическим
сосудом относительно его вертикальной
оси симметрии с постоянной угловой
скоростью ![]() ее
поверхность под воздействием центробежных
сил принимает форму параболоида вращения,
высота НП
которого определяется по формуле
ее
поверхность под воздействием центробежных
сил принимает форму параболоида вращения,
высота НП
которого определяется по формуле
![]() ,
,
а объем параболоида
![]() .
.
Когда при вращении жидкости ее свободная поверхность пересекает дно сосуда (см. рис. к задаче 1.2), указанный объем жидкости можно вычислить двояко:
![]() ,
или
,
или
![]()
где
![]() – радиус до положения свободной
поверхности жидкости на дне резервуара.
– радиус до положения свободной
поверхности жидкости на дне резервуара.
Зазор
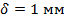 между валом и втулкой заполнен маслом
Ж.
между валом и втулкой заполнен маслом
Ж.
Длина втулки L. К валу, диаметр которого D приложен вращающий момент M. Определить частоту вращения вала при температуре масла T (рис. 5.3). Указание: при решении задачи применять формулу Ньютона.
Поскольку толщина слоя масла мала, можно считать, что скорости в нем изменяются по прямолинейному закону. Эпюра касательных напряжений в слое масла принимается прямоугольной; равнодействующая сил трения проходить через центр этой эпюры.
Рисунок
5.3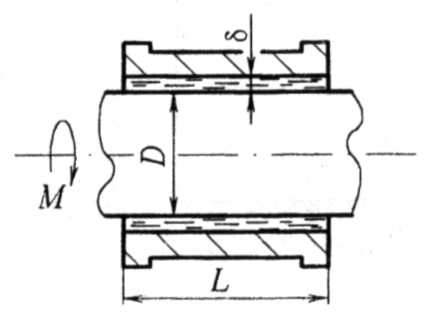
Закрытый резервуар заполнен дизельным топливом, температура которого
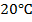 .
В вертикальной стенке резервуара
имеется прямоугольное отверстие (DxB),
закрытое полуцилиндрической крышкой.
.
В вертикальной стенке резервуара
имеется прямоугольное отверстие (DxB),
закрытое полуцилиндрической крышкой.
Она может повернуться вокруг горизонтальной оси A. Мановакуумметр MV показывает манометрическое давление PM или вакуум PВАК. Глубина топлива над крышкой равна Н, масса крышки m. Определить усилие F, которое необходимо приложить к нижней части крышки, чтобы она не открывалась (рис. 5.4).
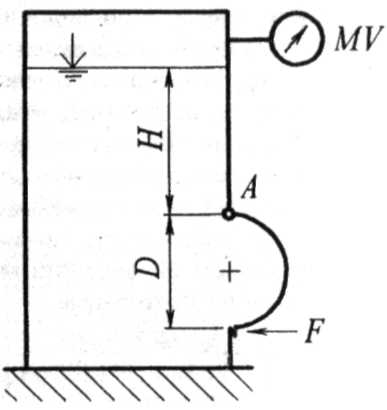
Рисунок 5.4
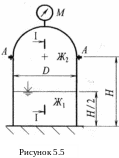
Вертикальная цилиндрическая цистерна с полусферической крышкой до самого верха заполнена двумя различными несмешивающимися жидкостями Ж1 и Ж2 (соответственно плотности ρ1 и ρ2). Диаметр цистерны D, высота ее цилиндрической поверхности H. Глубина жидкости Ж1 равна Н/2. Манометр М показывает манометрическое давление РМ. Определить силу, растягивающую болты А, и горизонтальную силу, разрывающую цистерну по сечению 1-1 (рис. 5.5)