Файловый архив студентов. Файловый архив студентов.
1302 вуза, 5135 предмета.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Брянский государственный технический университет
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:
2симестр_информатика_контрольная работа №1.doc
Скачиваний:
6
Добавлен:
14.09.2019
Размер:
1.37 Mб
Скачать
☆
►Содержание►

  1. Формирование функций проводимости для переключательных схем

В компьютерах и других автоматических устройствах широко применяются электрические схемы, содержащие сотни и тысячи пе­реключательных элементов: реле, выключателей и т. п. Разработка таких схем - весьма трудоемкое дело. Оказалось, что здесь с успе­хом может быть использован аппарат алгебры логики.

Переключательная схема это схематическое изображение некоторого устройства, состоящего из переключателей и соединяющих их провод­ников, а также из входов и выходов, на которые подается и с которых снимается электрический сигнал.

Каждый переключатель имеет только два состояния: замкнутое и разомкнутое. Переключателю X поставим в соответствие логичес­кую переменную х, которая принимает значение 1 в том и только в том случае, когда переключатель X замкнут и схема проводит ток; если же переключатель разомкнут, то х равен нулю.

Будем считать, что два переключателя X и связаны таким образом, что когда X замкнут, то разомкнут, и наоборот. Следователь­но, если переключателю X поставлена в соответствие логическая пере­менная х, то переключателю должна соответствовать переменная .

Всей переключательной схеме также можно поставить в соот­ветствие логическую переменную, равную единице, если схема про­водит ток, и равную нулю, если не проводит. Эта переменная явля­ется функцией от переменных, соответствующих всем переклю­чателям схемы, и называется функцией проводимости.

Найдем функции проводимости F некоторых переключательных схем:

а) схема не содержит переключателей и проводит ток всегда, следовательно, F = 1

;

б) схема содержит один постоянно ра­зомкнутый контакт, следовательно, F = 0

;

в) схема проводит ток, когда переключа­тель х замкнут, и не проводит, когда х разомкнут, следовательно, F(x) = х

;

г) схема проводит ток, когда переключа­тель х разомкнут, и не проводит, когда х замкнут, следовательно, F(x) =

;

д) схема проводит ток, когда оба переклю­чателя замкнуты, значит, F(x) = х • у

;

е) схема проводит ток, когда хотя бы один из переключателей замкнут, сле­довательно, F(x) = х v у

;

ж) схема состоит из двух параллельных ветвей и описывается функцией

F(x, у, z) = .

  1. Практические задания

Задание №1. Рассчитать значение выражения, используя табл. ответ записать в двоичной, шестнадцатеричной, десятичной системах счисления.

Аi • Вi - (Ci/Di + Bi • Сi) • Ai .

Таблица 5

i

A

B

С

D

1

1101110.01(2)

16.A3(16)

132(10)

35146.154(8)

2

1010101.11(2)

18.A4(16)

124(10)

14643.124(8)

3

1111000.11(2)

20.12(16)

346(10)

23535.234(8)

4

1100111.01(2)

14.BC(16)

567(10)

15352.235(8)

5

1010111.11(2)

12.CB(16)

235(10)

14754.246(8)

6

1110111.01(2)

13.CF(16)

234(10)

22635.235(8)

7

1001001.11(2)

15.FA(16)

346(10)

23563.422(8)

8

1110110.01(2)

16.FC(16)

345(10)

13454.564(8)

9

1001001.01(2)

13.BA(16)

656(10)

72234.235(8)

10

1011111.11(2)

1A.13(16)

756(10)

23523.534(8)

11

1100000.11(2)

1C.15(16)

376(10)

23125.532(8)

12

1000011.11(2)

1D.12(16)

578(10)

73451.235(8)

13

1001111.01(2)

1B.18(16)

426(10)

23555.235(8)

Продолжение таблицы 5

i

A

B

С

D

14

1111110.11(2)

1D.AF(16)

242(10)

23523.535(8)

15

1011111.01(2)

1A.CD(16)

857(10)

13341.323(8)

16

1101111.11(2)

16.AF(16)

856(10)

56235.235(8)

17

1011011.11(2)

18.AC(16)

497(10)

72455.235(8)

18

1011101.01(2)

20.1B(16)

876(10)

62523.235(8)

19

1101111.01(2)

14.BD(16)

364(10)

23523.532(8)

20

1101110.11(2)

12.CC(16)

969(10)

23553.353(8)

21

1010101.01(2)

13.CB(16)

446(10)

25356.352(8)

22

1111000.01(2)

15.FD(16)

352(10)

23546.235(8)

23

1100111.11(2)

16.F3(16)

244(10)

12435.252(8)

24

1010111.01(2)

13.B4(16)

374(10)

12412.214(8)

25

1110111.11(2)

1A.1B(16)

769(10)

15142.421(8)

26

1001001.01(2)

1C.1D(16)

255(10)

25346.356(8)

27

1110110.11(2)

1D.16(16)

475(10)

52354.323(8)

28

1001001.11(2)

1B.16(16)

568(10)

23235.235(8)

29

1011111.01(2)

1D.AB(16)

225(10)

41234.124(8)

30

1100000.01(2)

1А.СЗ(16)

134(10)

12415.155(8)

31

1000011.01(2)

16.AB(16)

548(10)

12421.412(8)

32

1001111.11(2)

18.A4(16)

790(10)

45432.153(8)

33

1111110.01(2)

20.16(16)

478(10)

13453.125(8)

34

1011111.01(2)

14.B7(16)

679(10)

23421.134(8)

35

1101111.11(2)

12.C8(16)

367(10)

14352.234(8)

Задание №2. Упростить формулы, используя (см. табл.6).

Таблица 6

i

а

b

с

d

e

j

g

1

X

Y

Y

Z

X

Y

Z

2

X

Z

Y

Z

X

Y

Y

Продолжение таблицы 6

i

а

b

с

d

e

j

g

3

Y

Z

X

Y

Z

Y

Z

4

X

Y

Z

X

Z

Y

Z

5

X

Z

Y

X

Y

Z

Y

6

Z

X

Z

Y

X

Z

Y

7

X

Z

Y

X

Z

X

Y

8

X

Y

Z

X

Y

X

Z

9

Z

Y

X

Y

X

Z

Y

10

X

Y

Y

Z

X

Y

X

11

Z

X

Y

Z

Y

X

Z

12

X

X

Z

Y

X

Z

X

13

Z

Y

X

Y

Z

X

Y

14

Z

Y

Y

Y

Z

X

Z

15

Y

Y

Y

Z

X

Y

Z

16

Y

X

X

Y

Z

Y

X

17

Y

Y

X

Z

X

Z

X

18

Z

X

Y

Z

Z

X

Z

19

Z

Y

X

Y

Z

Y

X

20

Y

Z

X

Y

Y

Z

Z

21

Z

Y

X

Y

X

Z

Y

22

X

Z

Y

X

Y

X

Z

23

X

Y

Y

Z

X

Y

Y

24

Y

Z

Y

X

Z

Y

Z

25

Z

Y

Z

X

Z

X

Z

26

X

Z

X

Y

X

Z

Z

27

X

Y

X

Y

X

Y

Z

28

Z

Y

X

Z

Y

X

Y

29

Y

Y

Z

X

Y

Z

Y

30

Z

Y

Y

Z

X

Y

Z

31

Z

X

Z

X

Z

X

Z

32

X

X

Z

Y

X

Y

X

33

Y

X

X

Z

Y

X

Y

34

X

Z

X

Y

Z

X

Z

35

X

Y

Z

X

Z

Y

X

Задание №3. Составьте логическое выражение (формулу), истинность которого обозначает попадание (принадлежность) точки с координатами (х,у) в выделенную на рис.3-7 область, включая ее граничные линии. Закрашенные области определены соответственно в табл. 7- 11.

1)

Рис.3

Таблица 7

№

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

1

2

3

4

5

6

7

8

2)

Рис.4

Таблица 8

№

1

2

3

4

5

6

7

8

9

10

11

12

13

14

1

2

3

4

5

6

7

8

3)

Рис.5

Таблица 9

№

1

2

3

4

5

6

7

8

9

10

11

12

13

14

1

2

3

4

5

6

7

8

4)

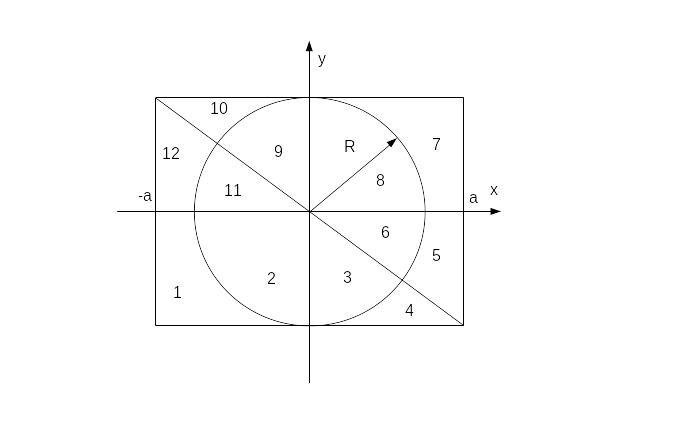
Рис.6

Таблица 10

№

1

2

3

4

5

6

7

8

9

10

11

12

1

2

3

4

5

6

7

8

5)

Рис.7

Таблица 11

№

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

1

2

3

4

5

6

7

8

Задание №4 Упростить переключательную схему.

1)

Таблица 12

№

1

2

3

4

5

6

1

Y

Z

X

2

X

Y

Z

3

Y

Z

X

Y

4

Y

Z

X

Z

5

X

Y

Y

Z

6

Z

Z

X

Z

7

X

Z

X

8

X

Y

X

2)

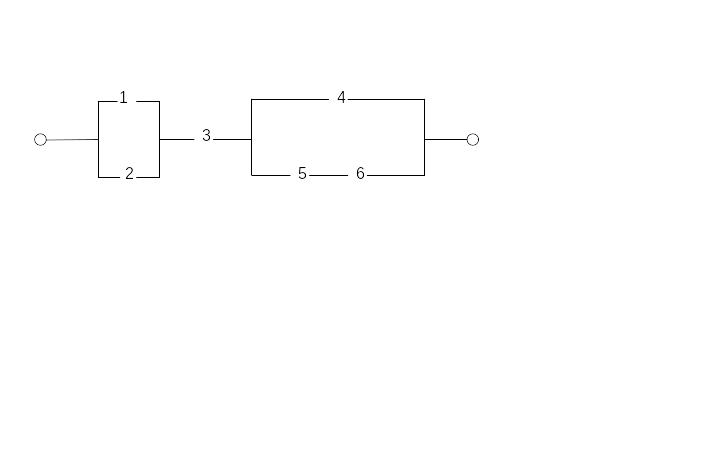
Таблица 13

№

1

2

3

4

5

6

1

Y

Z

X

2

X

Y

Z

3

Y

Z

X

Y

4

Y

Z

X

Z

5

X

Y

Y

Z

6

Z

Z

X

Z

7

X

Z

X

8

X

Y

X

3)

Таблица 14

№

1

2

3

4

5

1

Y

Z

t

2

X

t

Y

Z

3

Y

Z

t

4

Y

Z

X

Z

5

X

Y

t

Y

6

Z

t

Z

X

7

X

Z

t

8

X

t

X

4)

Таблица 15

№

1

2

3

4

1

Y

X

2

X

Y

X

3

Y

X

X

4

Y

X

5

X

Y

6

X

Y

7

X

X

8

X

Y

X

5)

Таблица 16

№

1

2

3

4

5

6

7

8

9

10

1

Y

Z

t

Y

Z

t

2

X

t

Y

Z

X

t

Y

Z

3

Y

Z

t

Y

Z

t

4

Y

Z

X

Z

Y

Z

X

Z

5

X

Y

t

Y

X

Y

t

Y

6

Z

t

Z

X

Z

t

Z

X

7

X

Z

t

X

Z

t

8

X

t

X

X

t

X

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности