Аналитический сигнал

Пусть есть сигнал s(t) определяемый как . Разделим его на две составляющие .

В том выражении –– аналитический сигнал. Если ввести переменную то . То есть мы получили . Реальный сигнал есть , сигнал сопряженный по Гильберту . Аналитический сигнал есть .

, –– прямое и обратное преобразование Гильберта.

Определение несущей и огибающей по методу Гильберта

Амплитуда сигнала , его фаза . Значение мгновенной частоты .

Пример: . .

–– точное определение огибающей. Использование метода Гильберта позволяет давать однозначные и абсолютно достоверные значения огибающей и мгновенной частоты сигнала.

–– любой сигнал можно разложить в ряд Фурье.

–– сопряженный по Гильберту сигнал.

Если сигнал представлен не рядом Фурье, а интегралом Фурье, то справедливы следующие соотношения , .

Свойства аналитического сигнала

1. 

   Спектр аналитического сигнала содержит только положительные частоты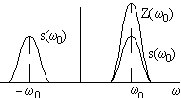

2. Произведение аналитического сигнала z_s(t) на сопряженный ему сигнал z_s^*(t) равно квадрату огибающей исходного (физического) сигнала s(t).

3. 

   Спектральная плотность комплексной огибающей совпадает со смещенной на величину w₀ влево спектральной плотностью аналитического сигнала z_s(t).

Иначе , где .

Преобразование Гильберта для узкополосного процесса

П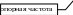 усть , тогда сопряженный по Гильберту сигнал .

Исходя из этого получим

Свойства преобразований Гильберта

––преобразование Гильберта, где Н( ) – оператор преобразования.

1. 

2. 

3. Если исходный сигнал s(t) имеет экстремум в какой-то точке, то в окрестности этой точки функция проходит через ноль.

Пример. Сигнал s(t) – идеальный низкочастотный сигнал.

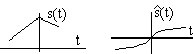
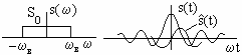
Частотные и временные характеристики

радиотехнических цепей

Пусть имеется линейный активный четырехполюсник.

1. Передаточная функция . Характеризует изменение сигнала на выходе относительно сигнала на входе. Модуль называют амплитудно-частотной характеристикой или просто частотной характеристикой. Аргумент –– фазо-частотная характеристика или просто фазовая.

2. Импульсная характеристика –– реакция цепи на единичный импульс. Характеризует изменение сигнала во времени. Связь с передаточной функцией осуществляется через обратное и прямое преобразование Фурье (соответственно) . Или же через преобразование Лапласа .

3. Переходная функция –– реакция цепи на единичный скачек. Это есть накопление сигнала за время t.

Апериодический усилитель

Схема замещения простейшего апериодического усилителя. Усилительный прибор представлен в виде источника тока SE₁ с внутренней проводимостью G_i=1/R_i. Емкость С включает в себя межэлектродную емкость активного элемента и емкость внешней цепи, шунтирующей нагрузочный резистор R_н.

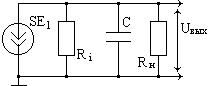
Передаточная функция такого усилителя

,

где S –– крутизна активного элемента, Е₁ – напряжение на входе.

Максимальный коэффициент усиления (при ) . Отсюда , где – время задержки.

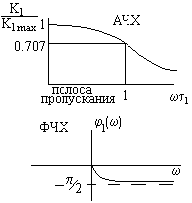
Модуль передаточной характеристики –– АЧХ. Т. е. этот усилитель пропускает сигнал только в определенной полосе частот. ФЧХ –– .