Изменение масштаба времени

Пусть сигнал s₁(t) подвергается сжатию во времени. Новый сигнал s₂(t) связан с исходным соотношением .

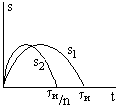
Длительность импульса s₂(t) в n раз меньше, чем исходного. Спектральная плотность сжатого импульса 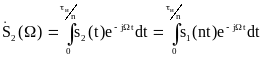. Введем новую переменную . Получим .

При сжатии сигнала в n раз во столько же раз расширяется его спектр. Модуль спектральной плотности при этом уменьшатся в n раз. При растяжении сигнала во времени имеют место сужение спектра и увеличение модуля спектральной плотности.

Смещение спектра колебаний

Домножим сигнал s(t) на гармонический сигнал cos(w₀t+q₀). Спектр такого сигнала

Разобьем его на 2 интеграла .

Полученное соотношение можно записать в следующей форме

Таким образом умножение функции s(t) на гармоническое колебание приводит к расщеплению спектра на 2 части, смещенные на ±w₀.

Дифференцирование и интегрирование сигнала

Пусть дан сигнал s₁(t) со спектральной плотностью S₁(W). Дифференцирование этого сигнала дает соотношение . Интегрирование же приводит к выражению .

Сложение сигналов

При сложении сигналов s₁(t) и s₂(t) обладающих спектрами S₁(W) и S₂(W) суммарному сигналу s₁(t)+s₂(t) соответствует спектр S₁(W)+S₂(W) (т. к. преобразование Фурье является линейной операцией).

Произведение двух сигналов

Пусть . Такому сигналу соответствует спектр

Представим функции в виде интегралов Фурье .

Подставляя второй интеграл в выражение для S(W) получим

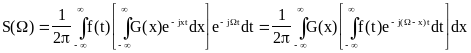
Следовательно .

Т. е. спектр произведения двух функций времени равен свертке их спектров (с коэффициентом 1/2p).

Если , то спектр сигнала будет .

Взаимная обратимость частоты и времени

в преобразовании Фурье

1. Пусть s(t) — четная функция относительно времени.

Тогда . Так как второй интеграл от нечетной функции в симметричных пределах равен нулю. Т. е. функция S(W) является вещественной и четной относительно W.

2. Пусть s(t) — нечетная функция относительно времени. При этом в нуль обращается первый интеграл и 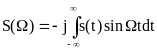. В этом случае S(W) является нечетной и чисто вещественной.

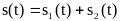3. Пусть . При этом 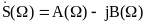, где А и В четная и нечетная функции соответственно.

Если предположить, что s(t) — четная функция. Запишем s(t) в виде . Произведем замену W на t и t на W, получим .

Если спектр имеет форму какого сигнала, то тогда сигнал соответствующий этому спектру повторяет форму спектра подобного сигнала.

Распределение энергии в спектре непериодического сигнала

Рассмотрим выражение , в котором f(t)=g(t)=s(t). В этом случае данный интеграл равен . Это соотношение носит название равенства Парсеваля.

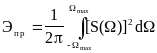Энергетический расчет полосы пропускания: , где , а .

Примеры спектров непериодических сигналов Прямоугольный импульс

Определяется выражением

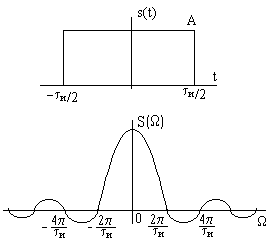
Найдем спектральную плотность

.

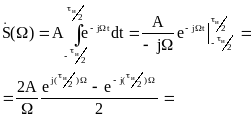
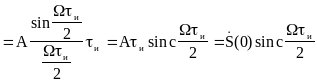При удлинении (растягивании) импульса расстояние между нулями сокращается, значение S(0) при этом увеличивается. Модуль функции можно рассматривать как АЧХ, а аргумент как ФЧХ спектра прямоугольного импульса. Каждая перемена знака учитывает приращение фазы на p.

При отсчете времени не от середины импульса, а от фронта ФЧХ спектра импульса должна быть дополнена слагаемым , учитывающим сдвиг импульса на время (результирующая ФЧХ показана пунктиром).