2. Гидродинамическое описание физической среды. Гидродинамическая система уравнений описания среды как выражение законов сохранения массы, импульса и энергии в системе.

Гидродинамическое описание среды можно получить из уравнения Больцлана

Использовав некоторые традиционные определения

Вместо концентрации следует использовать отличающуюся от нее лишь множителем (масса частицы) плотность :

Микроскопическую скорость определим, естественно, равенствами

Используя тепловую скорость , определим внутреннюю энергию :

тензор напряжений :

и вектор плотности потока тепла :

Тогда гидродинамическое описание сведется к трем уравнениям

Каждое из уравнений, входящих в гидродинамическую систему, имеет дивергентный вид и выражает, соответственно, закон сохранения массы, импульса и энергии.

2. ОПИСАНИЕ ФИЗИЧЕСКОЙ СРЕДЫ, ОСНОВАННОЕ НА МОДЕЛИ ИДЕАЛЬНОГО ГАЗ. Понятие «идеальная газовая среда». Физические предпосылки. Основные свойства идеального газа. Модельная система уравнений. Одномерная постановка.

Гидродинамическое описание сведется к трем уравнениям

Каждое из уравнений, входящих в гидродинамическую систему, имеет дивергентный вид и выражает, соответственно, закон сохранения массы, импульса и энергии.

Однако система незамкнута – неизвестных больше чем уравнений. Необходимы дополнительные соображения для получения замкнутой модели.

Существует традиционное упрощение этой системы, основанное на понятии «идеальной газовой среды» («идеального газа»). Самым простым и естественным является предположение о независимости функции распределения в каждой точке от направления местной тепловой скорости . Это означает, что

В этом случае недиагональные элементы тензора напряжений

и компоненты вектора плотности потока тепла :

равны нулю как интегралы от нечетных функций. Диагональные элементы

одинаковы. Таким образом,

причем давление определяется по формуле

Такая модель носит название – модель «идеального газа». В ней остается пять функций:

• три компоненты скорости ,

• плотность массы 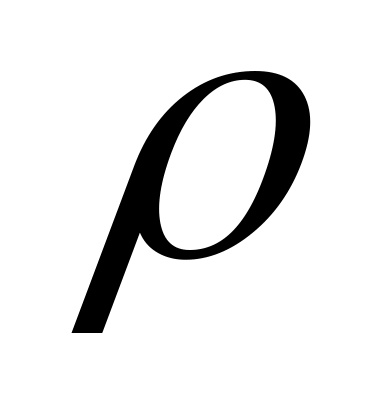и

• внутрен­няя энергия .

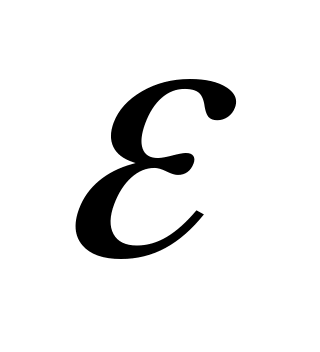Наиболее простым вариантом является одномерный, когда все функции зависят только от одной пространственной координаты , т.е. и движение по отсутствует, т.е. . Уже в этом, одномерном случае проявляются многие интересные особенности модели.

С учетом введенных упрощений система приобретет вид

где

— заданная функция, например , но необязательно.

Система выражает законы сохранения (массы, импульса, энергии) и, естественно, имеет дивергентную форму потому что такую форму имеет газодинамическая система уравнений из которой это все выведено. Несложными преобразованиями ее можно привести к более простому, стандартному для квазилинейных систем виду

Обозначив тройку функций вектор-функцией , последнюю систему можно записать в виде одного векторного уравнения

с матрицей

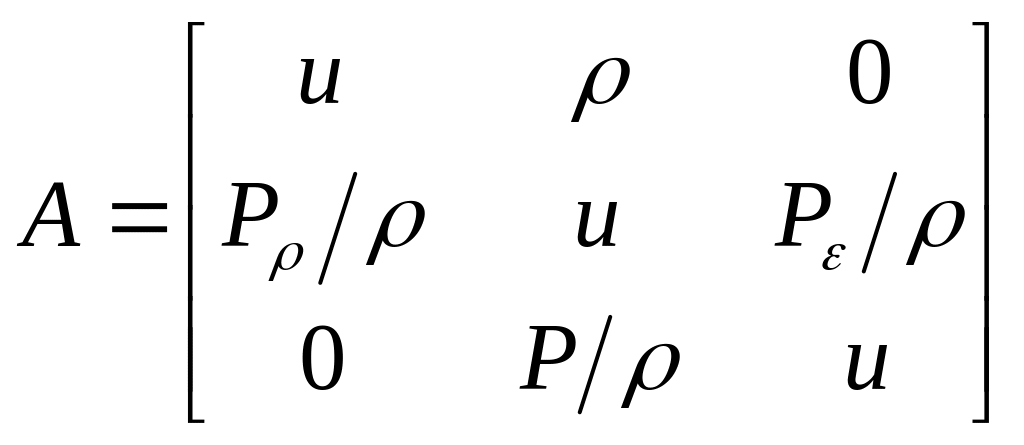
где — частные производные функции (6.4).

Задача всегда содержит условия на границах области, при решении конкретной задачи их надо учесть.