2.4.4. Модели бинарного выбора

В теме фиктивные переменные рассматриваются модели, в которых какие-либо независимые переменные принимают дискретные значения. Например, 0 и 1, выражая некоторые качественные признаки относительно зависимой переменной. Явно или неявно предполагалось, что она выражает количественный признак, принимая непрерывное множество значений, но довольно часто интересующая нас величина по своей природе является дискретной.

Рассмотрим несколько типичных ситуаций.

1 блок. Выбор из двух или нескольких альтернатив (голосование ,например , решение работать или не работать, покупать или не покупать, выбор профессии, способ попадания из дома на работу).

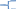x_t= 1

0

Когда есть две возможности, т.е. бинарный выбор и результат наблюдаемый можно описать с помощью 1 и 0, то переменную называют бинарной.

Если есть выбор из k альтернатив (нескольких), то переменную называют номинальной, если альтернативы нельзя естественным образом упорядочить. Последние и предпоследние примеры – номинальные переменные.

2 блок. Ранжированный выбор.

Есть несколько альтернатив, но они некоторым образом упорядочены. Например, доходы семьи (высокие, низкие, средние), уровень образования (высшее, среднее), состояние здоровья (плохое, удовлетворительное, нормальное).

Т акие переменные называются порядковыми (ранговыми).

1

x_t= 2

…

k

3 блок. Количественная целочисленная характеристика.

Например, количество прибыльных предприятий, количество зарегистрированных патентов в течение года.

Для моделей с дискретными зависимыми переменными МНК применить достаточно сложно.

Для рассмотрения первого типа ситуаций(для бинарных переменных) можно применить модели бинарного выбора.

Модели с несколькими альтернативами можно свести к моделям бинарного выбора или исследовать аналогичные методы.

Другой класс моделей, рассматриваемый для качественных переменных, связан с цензурированными или урезанными выборками.

Пусть имеется общая модель линейной регрессии:

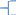y_t=x₁^/β+ε

y_t=1

0

M(ε_t)=0

P(y_t=1)=x_t^/β - линейная модель вероятности

Если в качестве уравнения выбрать функцию

P(y_t=1)*F(x_t^/*β), где F – некоторая функция, область значений которой лежит в отрезке от 0 до 1.

Предположим, что существует некая количественная переменная y_t*, связанная с независимыми переменными x_t в обычном регресионном уравнении. Например, y_t*=x_t^/*β+ε

Решение соответствующих значений y_t=1 принимается тогда, когда y_t* превосходит некоторые пороговые значения:

y_t=1, если y_t*=у пороговое;

y_t=0, если y_t= у пороговое

Если в качестве F используется функцию стандартизированного нормального распределения, то соответствующую модель называют probit-моделью.

Если в качестве F используется функцию логистического распределения, то соответствующую модель называют logit-моделью.

3.1.Виды нелинейной зависимости

3.1.1.Основные понятия

Зависимость между теми или иными факторами в эконометрике не всегда можно описать с помощью линейной функции. В этом случае применяют нелинейную регрессию. Общий вид:

y_расч=f(x₁) – для однофакторной регрессии

y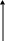 _расч=f(x₁,x₂,…,x_p) – для многофакторной регрессии

a>1

a<1

Для перехода к линейному виду, уравнение логарифмируют по основанию a:

log_ay=log_aa^bx+ε=bx+ ε

log_ay=bx+ ε

Заменим зависимую переменную log_ay на z:

z= bx+ ε

Частный случай экспоненциальной зависимости – логистическая кривая:

Д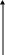 анная кривая имеет 2 горизонтальные асимптоты y=o, y=1/a и точку перегиба

1/a

1/2a

1/(a+b)

Логистические кривые используются для описания поведения показателей, имеющих определенные уровни насыщения (например, для описания зависимости спроса на товар от дохода).

Линеаризация этой зависимости проводится с помощью перехода к переменным

e^x=t; . Получаем: z=a+bt+ε

З ависимости логарифмического типа имеют вид

a>1

a<1

Обозначим log_ax=z. Получим линейную модель:

Зависимости полиномиального вида:

y=a+b₁x+b₂x²+…+b_px^p+ε

Обозначим x=z₁, x²=z₂,…, x^p=z_p

y=a+b₁z₁+b₂z₂+…+b_pz_p+ ε

Зависимости степенного вида

y=ax^b

Прологарифмируем по основанию e:

ln(y)=ln(a)+b*ln(x)

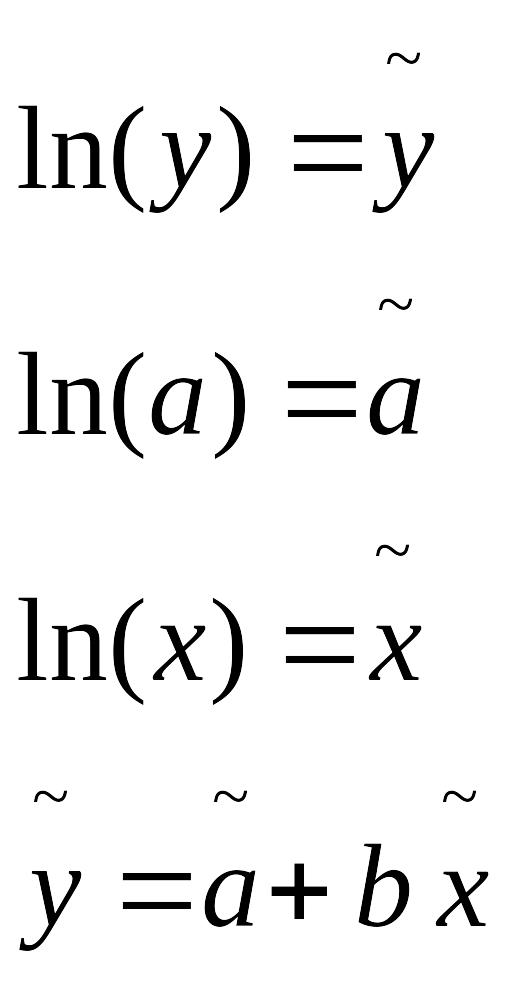
Если модель по независимым факторам является мультипликативной, то переход к аддитивной модели и как следствие к линейной осуществляется с помощью логарифмирования всей зависимости