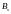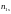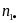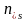13. Коэффициент корреляции Пирсона: содержательный смысл, формула расчета. Проблема устойчивости. Примеры применения в политологии (прошлый год)

Общие положения

• Коэффициент корреляции: ; причем ковариация случайных величин и равна _{(разность математического ожидания произведения случайных величин и произведения математических ожиданий каждой величины)}

• Смысл: коэффициент корреляции показывает меру связи случайных величин;

• Область значений коэффициента (допустимые значения): [-1;1];

  • отрицательные значения – отрицательная связь (монотонно убывающая);

  • если коэффициент корреляции равен -1 или 1, то тогда величины и линейно связаны, то есть таким и , что

  • для независимых случайных величин коэффициент корреляции (если он существует), равен нулю.

Коэффициент корреляции Пирсона

• Расчетная формула:

• Проверка равенства коэффициента нулю: есть ли основания полагать, что посчитанное нами число значимо отличается от 0.

  • надо посчитать граничные точки и - , между которыми будет меняться нулевой коэффициент корреляции.

  • (n – размер одной из выборок);

  • смотрим по таблицам Стьюдента и считаем , потом смотрим, куда попал коэффициент Пирсона;

• Проблема: чувствительность к выбросам – нетипичным, резко выделяющимся наблюдениям.

• Пример в политологии: связь политических предпочтений с чем угодно – пол, возраст, вес. Например, за Путина голосовали толстые

15. Изучение связи качественных признаков: анализ таблиц сопряженности. Внешний вид таблицы сопряженности. Статистические средства анализа таблицы сопряженности: критерий χ² К.Пирсона. Примеры применения в политологии. (прошлый год)

• Анализ таблиц сопряженности используется для выявления связи между двумя качественными признаками. У каждого из них есть конечное число «значений». (Например, для признака «пол» значения «мужской» и «женский»).

Таблица сопряженности:

A\B

• Величины n в правом крайнем столбце – суммы значений n по строкам,

• Величины n нижней строки таблицы – суммы по столбцам

• В правом нижнем углу - общая сумма всех наблюдений, необходимая для подсчета вероятностей.

• Смысл всего анализа - сопоставить ожидаемые (теоретические) вероятности и наблюдаемые (практические).

• Алгоритм действий

1. Выдвигаем гипотезу о независимости признаков:

2. Вычисляем ожидаемые частоты по формуле

(произведение сумм по строкам и сумм по столбцам; ожидаемые потому что при условии выполнения гипотезы)

3. Вычисляем наблюдаемую вероятность по формуле:

4. Мерой согласия опытных данных с теорией будет критерий хи-квадрат. Число степеней свободы считается по формуле , то есть для матрицы два на два, будет одна степень свободы

5. Считаем величину, по следующей формуле:

6. Полученную сумму (получается, что для каждой клеточки считаем мегадробь, а потом их суммируем) сравниваем с верхней процентной точкой (есть специальные таблицы). Если полученное значение больше, то гипотеза отвергается и у наших признаков есть связь, они зависимы.

• Пример использования: есть ли связь между полом и голосованием за какого-то кандидата (в столбцы загоняем пол – мужской/женский, а кандидатов в строки – Путин, Медведев, Зюганов; в столбики забиваться будет количество людей, проголосовавших за одного из этих парней)

Вопрос №16.

Простая линейная регрессия: постановка задачи, графическая интерпретация. Метод наименьших квадратов и МНК-оценки коэффициентов модели. Коэффициент детерминации. Проверка гипотез о коэффициентах при предикторах и качестве модели. (Бочарова А)

Регрессия. 1862 г. Sir Francis Galton “Regression towards Mediocrity hereditary stature”.

Психометрика, биология, коэффициент корреляции.

i	yi	xi
1	y1	x1
2	y2	x2
3	y3	x3
…	…	…
n	yn	xn

Задача парной регрессии – описание изменчивости y с помощью изменчивости x.

Y – отклик, эндогенная переменная.

X – предиктор, регрессор, ковариата, фактор, экзогенная переменная.

Линейная регрессия:

y_i = β₀ + β₁ * x_i + ε_i – уравнение парной линейной регрессии (простой линейной регрессии).

[Например, x – уровень урбанизации, y – поддержка партии КПРФ] по регионам РФ.

Точки – регионы РФ.

Описать взаимосвязь x и y в среднем.

Понять, чему в среднем будет равен y, если x равен конкретному числу.

Задача – построить прямую, которая будет лежать максимально близко к точке, т.е. наименьшие отклонения.

y_i = β₀ + β₁ * x_i + ε_i

|________|

y_{i с} крышкой= β₀ + β₁ * x_i – все лежат на прямой, т.к. это уравнение прямой.

|

Это прогнозный отклик.

Мат. ожидание отклика при должном значении предиктора.

y_i с крышкой = E (y|x_i)

y_i = y_i с крышкой + e_i

e_i – ошибка, остаточный член, случайный член (графически это вертикальная палочка до прямой регрессии).

Наша цель – подобрать такие β₀ и β₁, чтобыпрямаялежала наиболее близко к точкам.

1821 – 1822гг. – МНК.

y_i = β₀ + β₁ * (x_i – x _ср.) + ε_i

Для того чтобы перенести ось в точку среднего значения x из точки (0;0).

Лаплас предложил использовать модули, чтобы отрицательные значения не гасили положительные.

НО: этот метод тогда не стал востребованным, поскольку не умели дифференцировать в точке минимуму = |x|.

Тогда К. Гаусс предложил брать квадраты.

Ψ = ∑ e_i² → min

Ψ = ∑ (y_i – β₀ – β₁ (x_i – x _ср.))² → min

β₀, β₁

Ищем производную и приравниваемее к нулю, т.к. производная это тангенс угла наклона касательной к графику.

Решаем систему уравнений:

Ψ_β0 = ∑ (– 2 (y_i – β₀ – β₁ (x_i – x _ср.))) = 0

Ψ_β1 = ∑ (– 2 (y_i – β₀ – β₁ (x_i – x _ср.))) (x_i – x _ср.) = 0

Решаем уравнения по отдельности. Сначала первое.

Ψ_β0 = ∑ (– 2 (y_i – β₀ – β₁(x_i – x _ср.))) = 0

Сокращаем на минус два.

∑ y_i – nβ₀ – β₁∑ (x_i – x _ср.) = 0

Учитываем, что β₁∑ (x_i – x _ср.) = 0,

т.к. x _ср. = ∑ x_i /n,

∑ x_i = nx _ср.

∑ (x_i – x _ср.) = ∑ x_i – x _ср.n = x _ср.n – x _ср.n = 0

Тогда

∑ y_i – nβ₀ = 0

β0 мнк с крышкой = ∑ yi / n = уср.

МНК-оценка β₀ – наша оценка значения β₀ с помощью МНК, МНК-оценка первого коэффициента модели.

МНК-оценка β₁

Решаем второе уравнение из системы.

Ψ_β1 = ∑ (– 2 (y_i – β₀ – β₁ (x_i – x _ср.))) (x_i – x _ср.) = 0

Сокращаем на минус два.

∑ ((y_i – y _ср.) *(x_i – x _ср.) – β₁ (x_i – x _ср.)²) = 0

∑ ((y_i – y _ср.) *(x_i – x _ср.)) – β₁ ∑ (x_i – x _ср.)² = 0

β1 мнк с крышкой = ∑ ((yi – y ср.) *(xi – x ср.)) / ∑ (xi – x ср.)2

β₁ ^мнк с крышкой = R * (∑ (y_i – y _ср.)² )^0,5 / (∑ (x_i – x _ср.)²)^0,5,

где R – коэффициент корреляции Пирсона.

Рассмотрим на примере.

Допустим,

β₀ ^мнк с крышкой = 25

β₁ ^мнк с крышкой = 0,7

yi = 25 + 0,7xi + exi

yi с крышкой = 25 + 0,7xi

Интерпретации МНК-оценок коэффициентов модели

Интерпретация β₁ ^мнк с крышкой.

С ростом x на единицу y в среднем при прочих равных условиях увеличивается на 0,7.

Интерпретация β₀ ^мнк с крышкой.

Если x = 0, то в среднем при прочих равных условиях y = 25.

Позволяет нам прогнозировать. И показать, насколько у зависим от x.

В классическом подходе мы рассматриваем x_i как неслучайную, детерминированную величину, а y_i как случайную.

За счет чего? За счет случайности e_i.

Предположения Гаусса – Маркова на e_i.

1. e_i – случайная величина, у которой E(e_i) = 0.

y_i = β₀ + β₁x_i + e_i,

где β₀ + β₁x_i – условное мат. ожидание. И для этого среднее ei должно быть равно 0!

2. e_i – случайная величина, у которой D(e_i) = ς₁² = ς₂²

Предположение о гомоскедастичности остатков.

Гетероскедастичность – с ростом (убыванием) x, разброс остатков растет (убывает).

– с уменьшением x, уменьшается разброс. Есть зависимость остатков от предиктора, это значит, что мы в модели учли не все.

Гомоскедастичность – нет зависимости.

3. Corr (ei; ej) = 0 для любого i≠j. Предположение об отсутствии АК.

4. Corr (ei; xi) = 0.

Нет корреляции остатка и предиктора (т.е. с ростом x растет сам остаток или с уменьшением – уменьшается).

И еще одно предположение отдельное (не входит в набор Гаусса-Маркова):

5*. Ei ~ N (0; ς²). Это значит, что все значимое в модели мы учли.

Теорема Гаусса – Маркова.

Если выполняются четыре предположения, то МНК-оценки – наилучшие линейные несмещенные оценки.

Если мы предполагаем случайность величин оценок β₀ ^мнк с крышкой и β₁ ^мнк с крышкой, то они распределены нормально.

β₀ ^мнк с крышкой ~ N (β₀; ς²/n)

β₁ ^мнк с крышкой ~ N (β₁; ς²/∑ (x_i – x _ср.)²)

А β₀ ^мнк и β₁ ^мнк сами по себе константы и никакого распределения не имеют.

Насколько хороша модель?

Показателем качества модели является коэффициент детерминации.

[Может, сам x был неверно выбран? Т.е. не уровень урбанизации объясняет голосование за КПРФ, а что-то другое надо было брать].

Коэффициент детерминации – R² = квадрат коэффициента корреляции Пирсона между x и y.

F – критерий.

H0: достаточно константы (модель плоха).