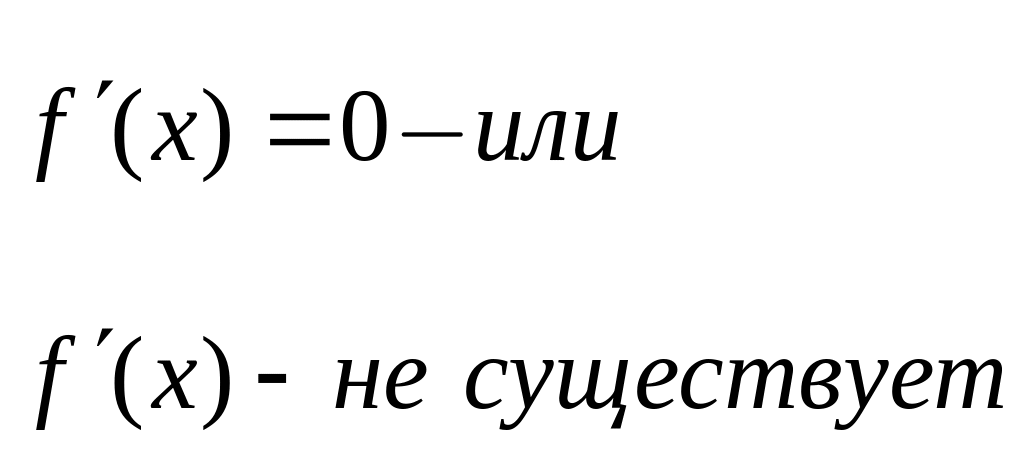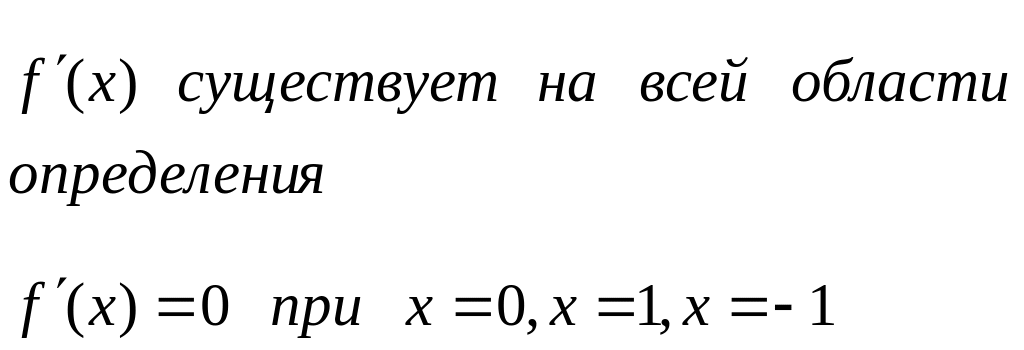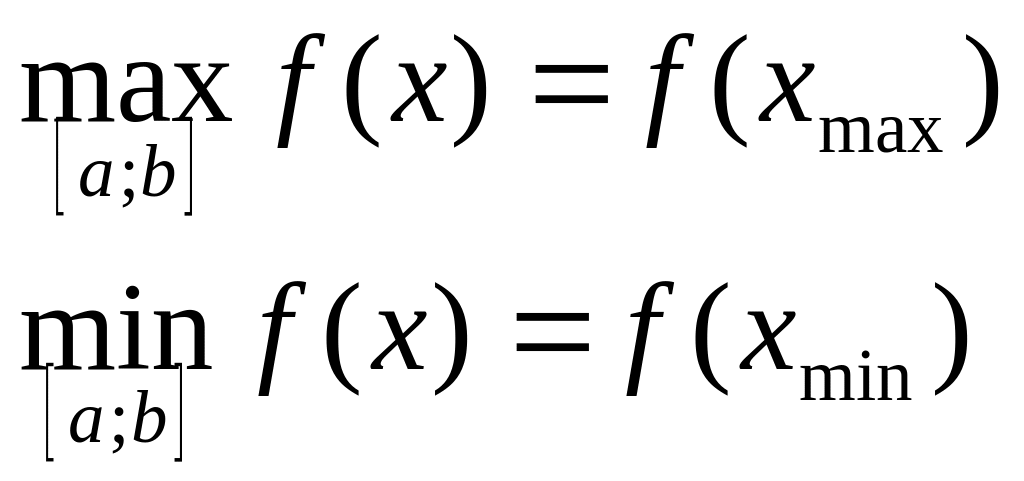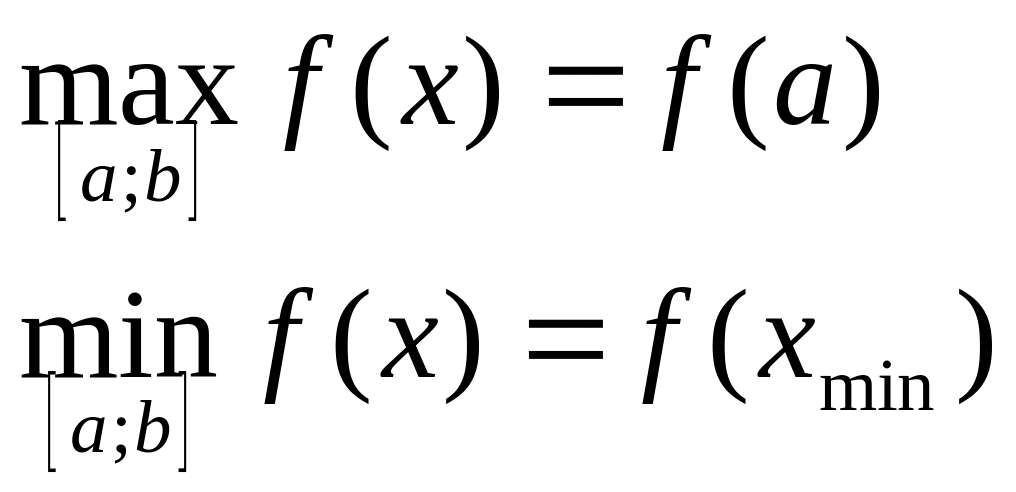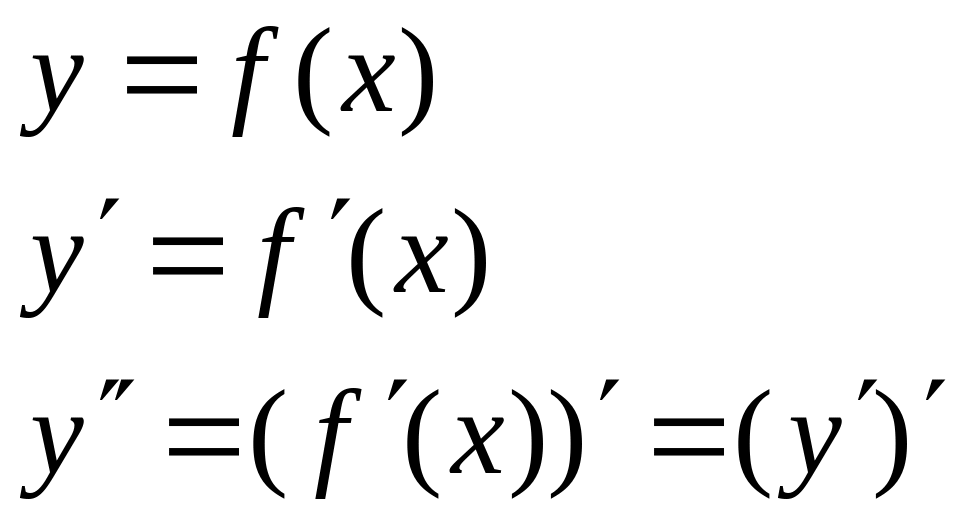- •1. Область определения функции:
- •3. Точки пересечения с осями координат.
- •4. Производная и критические точки.
- •1. Область определения функции:
- •3. Точки пересечения с осями координат.
- •4. Производная и критические точки.
- •1. Область определения функции:
- •3. Точки пересечения с осями координат.
- •4. Производная и критические точки.

1. Область определения функции.
2. Четность, нечетность, периодичность.
3. Точки пересечения с осями координат.
4. Производная и критические точки.
5. Промежутки возрастания, убывания и точки экстремума и значение функции в этих точках.
6. Поведение функции на концах области определения и асимптоты графика функции (вертикальные, горизонтальные, и наклонные)
7. Вторая производная и исследование функции на выпуклость и вогнутость, и нахождение точек перегиба.
8. Нахождение контрольных точек.
9. Построение графика по результатам исследования.
Приложения.
Таблица 1. Как найти область определения функции.
Таблица 2. Четные и нечетные функции.
Таблица 3. Периодические функции.
Таблица 4. Применение производной к исследованию функции.
Таблица 5. Асимптоты графика функции.
Таблица 6. Вторая производная и точки перегиба.
Примеры.
Пример
1. Исследовать
функцию
![]() и построить график функции.
и построить график функции.
Пример
2. Исследовать
функцию
![]() и построить график функции.
и построить график функции.
Пример
3. Исследовать
функцию
![]() и построить график функции.
и построить график функции.
Схема исследования функции y = f(x) для построения эскиза ее графика. |
|||||||
Схема |
Пример
|
||||||
1. Область определения функции (см. табл. 1) |
Область определения:
|
||||||
2. Четность, нечетность (табл. 2), периодичность (табл. 3) |
Функция ни четная, ни нечетная и не периодическая |
||||||
3. Точки пересечения с осями координат (если можно найти)
|
0y |
||||||
y = 0;
0x |
|||||||
4. Производная и критические точки (табл. 4)
|
|
||||||
|
|||||||
5. Промежутки возрастания, убывания и точки экстремума (и значение функции в этих точках) (табл. 4)
|
|
||||||
6. Поведение функции на концах области определения и асимптоты графика функции (вертикальные, горизонтальные, и наклонные) (табл. 5)
|
П
При справа x = - 4
Так как
то при
тогда
т.е. y = x - 9 - наклонная асимптота
|
||||||
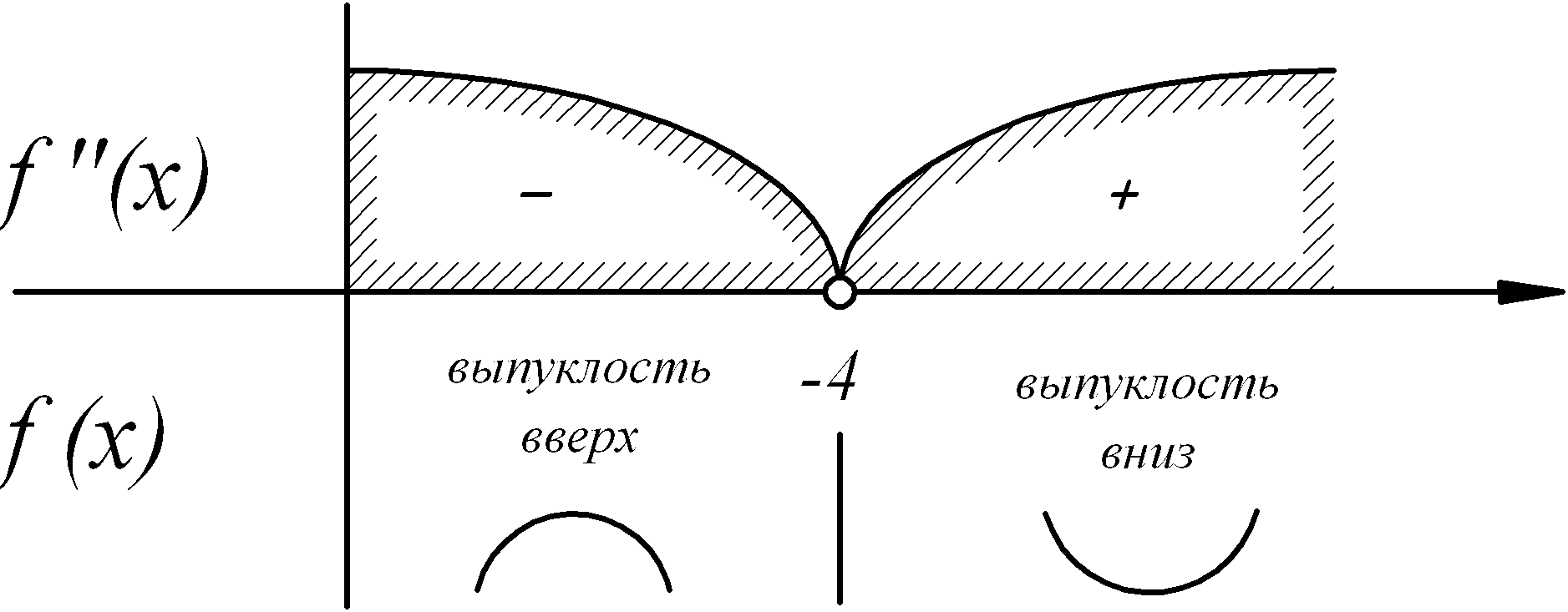
7. Вторая производная и исследование функции на выпуклость и вогнутость. Найти точки перегиба (если они существуют) и значение f(x) в точках перегиба (табл. 6)
|
П |
||||||
|
X
-6
-2
Y
-33
7 |
||||||
|
|
||||||
Как найти область определения функции |
|||
№ |
Вид функции |
Ограничения (f(x) и g(x) существуют!) |
Формулировка |
1 |
|
|
Знаменатель дроби не равен нулю |
2 |
|
|
Под знаком корня четной степени может стоять только неотрицательное выражение |
3 |
|
|
Под знаком логарифма может стоять только положительное выражение |
4 |
(a >0) |
|
В основании логарифма может стоять только положительное выражение, не равное 1 |
5 |
|
|
Под знаком котангенса может стоять
только выражение, не равное
|
6 |
|
|
Под знаком котангенса может стоять
только выражение, не равное
|
7 |
|
|
Под знаком арксинуса и арккосинуса может стоять только выражение, модуль которого меньше или равен единице |
8 |
|
||
9 |
|
|
|
а)
|
x – любое число |
||
б) - целое отрица-тельное или нуль |
|
||
в) - положитель-ное не целое число |
|
||
г) - отрицатель-ное не целое число |
|
||
Таблица 1
Таблица 2
Четные и нечетные функции |
|
Четная функция |
Нечетная функция |
Определение. Функция f называется четной, если ее область определения симметрична относительно начала координат и для любого X из ее области определения
|
Определение. Функция f называется нечетной, если ее область определения симметрична относительно начала координат и для любого X из ее области определения
|
Свойства |
Свойства |
График четной функции симметричен относительно оси 0y |
График нечетной функции симметричен относительно начала координат |
Примеры четных функций |
Примеры нечетных функций |
|
|
|
|
Таблица 3
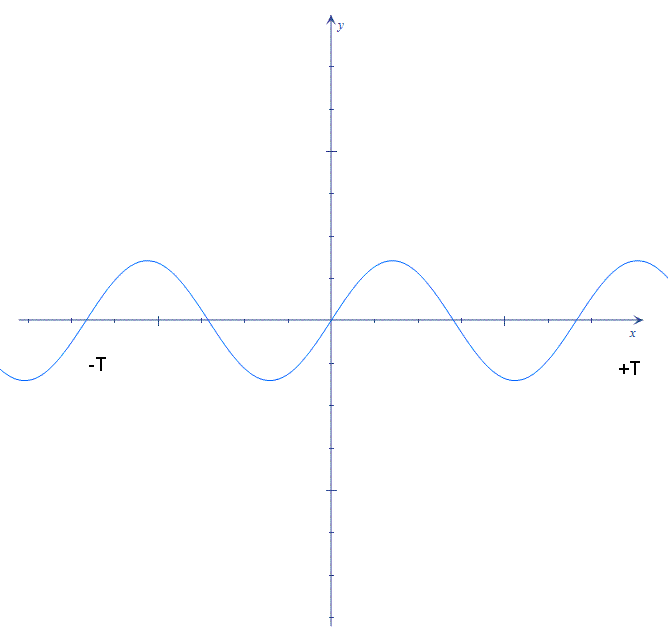
Периодические функции |
|||
Определение.
Функция называется периодической
с периодом
|
|||
Свойства |
|||
1. Если число Т период функции f
, то число
k*T
|
|||
2. Если функция y=f(x)
периодическая с периодом Т, то
функция y=Af(kx+b)
также периодическая и ее период
равен
|
|||
3. Если функция y=f(x) периодическая с периодом Т, то сложная функция (функция от функции) y=φ(f(x)) также периодическая с периодом Т (хотя, возможно, этот период и не является наименьшим по абсолютной величине) |
|||
4. Для построения графика периодической
функции с периодом Т достаточно
построить график на отрезке длиной
Т, а далее – параллельно перенести
этот график вдоль оси 0х на расстояние
|
|||
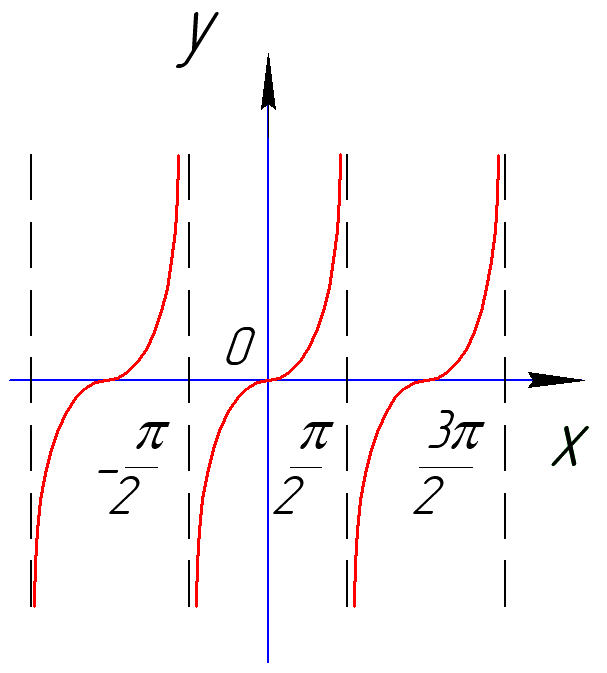
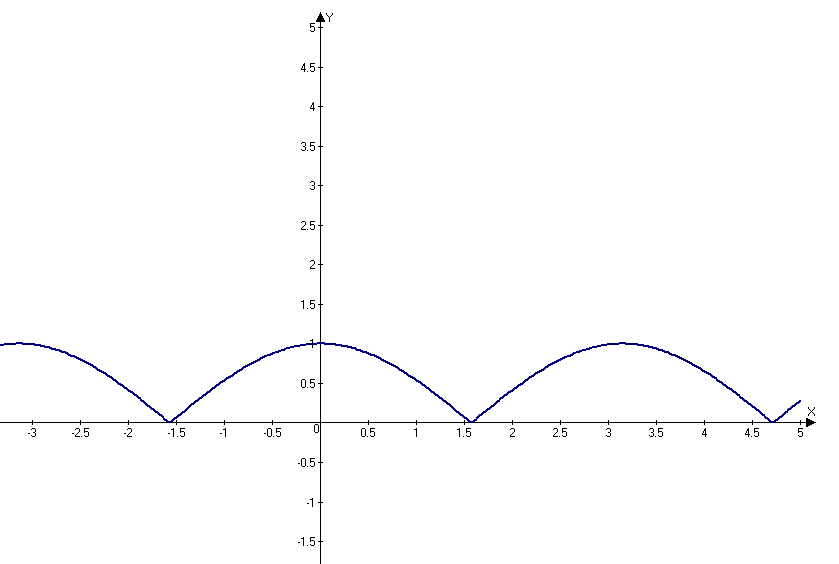
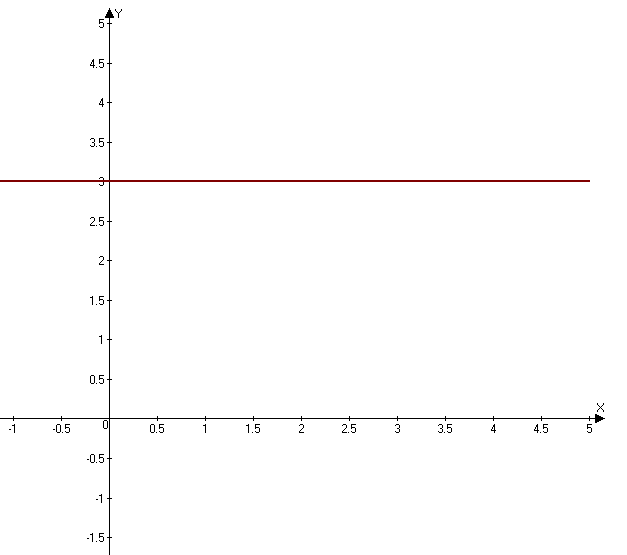
Примеры периодических функций |
|||
y=sin(x) T=2π
|
y=cos(x) T=2π
|
y=tg(x) T=π
|
y=ctg(x) T=π
|
y=sin(3x)
T=
|
y={x}- дробная часть х T=1
|
y=|cos(x)| T=π
|
y=3 T-любое число (Т≠0)
|
Практические приемы нахождения периодов функций |
|||
1. Найти период каждой составляющей функции, которая входит в запись заданной функции. 2. Подобрать интервал (если возможно), внутри которого каждый из найденных периодов укладывается целое число раз. Длина этого интервала и будет периодом заданной функции (хотя, возможно, и не наименьшим по абсолютной величине). Пример:
f(x) =
sin(4x)+tg(3x);
|
|||
Таблица 4
Применение производной к исследованию функции |
|||
Монотонность и постоянство функции |
|||
Достаточное условие возрастания функции |
Достаточное условие возрастания функции |
||
Если в каждой точке интервала (a;b) ƒ ́(x)>0, то функция ƒ(x) возрастает на этом интервале |
|
Если в каждой точке интервала (a;b) ƒ ́(x)<0, то функция ƒ(x) убывает на этом интервале |
|
З но не являются необходимыми условиями возрастания
и убывания функции.
Например,
функция
на всей области определения, хотя в точке
|
|||
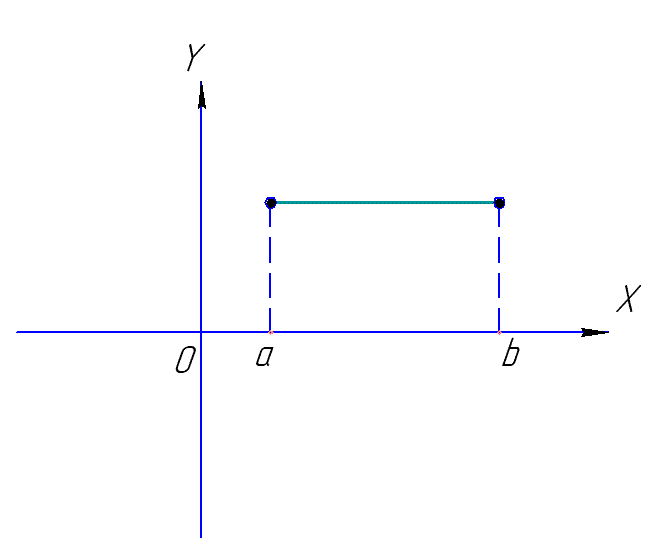
Необходимое и достаточное условие постоянства функции |
|||
Функция
|
|||
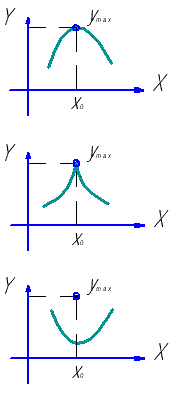
Экстремумы (максимум и минимум) функции |
|
Точка максимума |
Точка минимума |
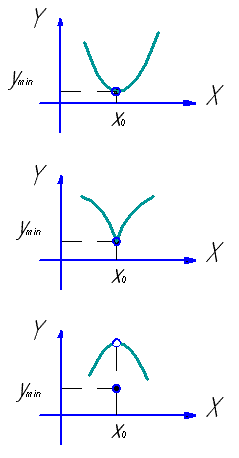
Определение Точка
определения
функции
называется точкой максимума для этой функции, если найдется
( т |
Определение Точка из области определения функции называется точкой минимума для этой функции, если найдется - окрестность ( |
|
|
Точки максимума и минимума называются точками экстремума. Значения функции в точках максимума и минимума называются экстремумами функции (максимумом и минимумом функции) |
|
|
|
Критические точки |
|
Определение. Внутренние точки области определения функции, в которых производная функции равна нулю или не существует, называются критическими. |
|
Необходимое условие экстремума |
Достаточное условие экстремума |
В точках экстремума
производная функции
равна нулю или не существует
- точка экстремума
|
Если функция
непрерывна
в точке
и
производная
в точке знак меняется с «+» на «-» - точка максимума
в точке знак меняется с «-» на «+» точка минимума |
Пример графика функции , имеющей экстремумы ( |
|
|
|
Исследование функции
|
|
Схема |
Пример
|
1. Найти область определения и интервалы, на которых функция непрерывна |
Область определения:
Функция непрерывна в каждой точке своей области определения |
2. Найти производную
|
|
3. Найти критические
точки, т.е. внутренние точки области
определения, в которых
|
|
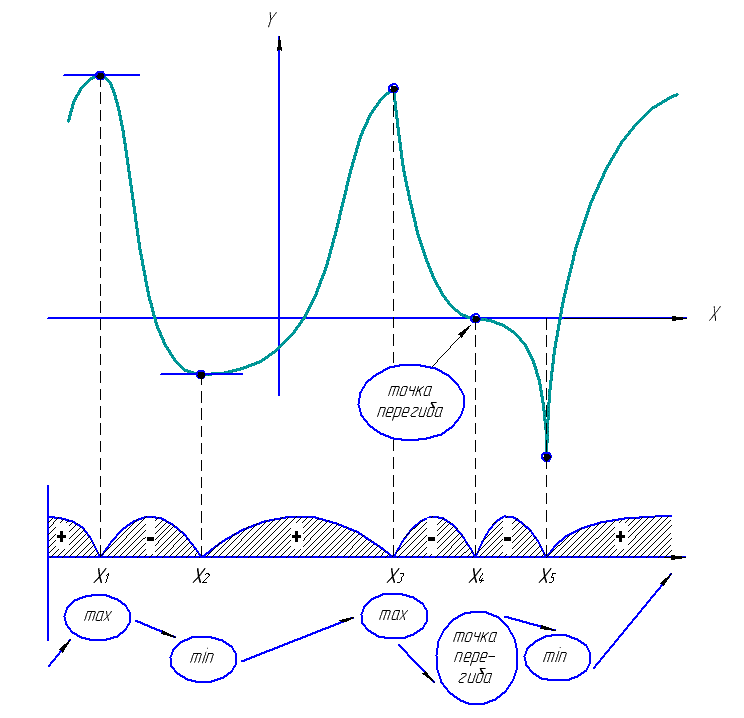
4. Отметить критические точки на области определения, найти знак производной и характер поведения функции на каждом интервале, на которые разбивается область определения. |
|
5. Относительно каждой критической точки определить, является ли она точкой максимума, минимума или не является точкой экстремума |
|
6. Записать требуемые результаты исследования (промежутки монотонности и экстремумы) |
возрастает
при
при
|
убывает
при
|
|
Точки экстремума:
Экстремумы:
|
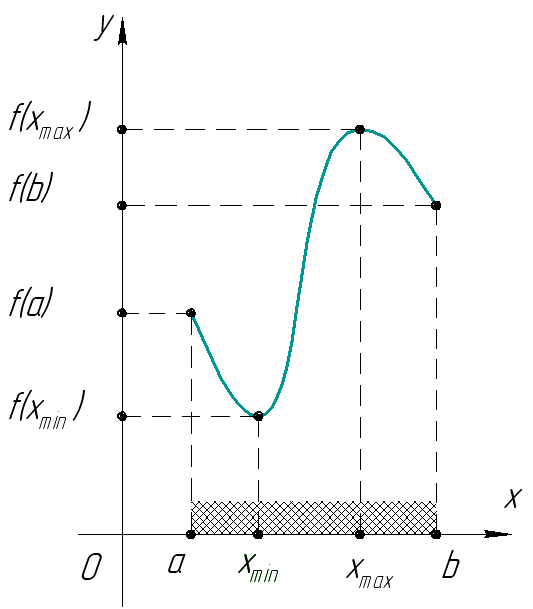
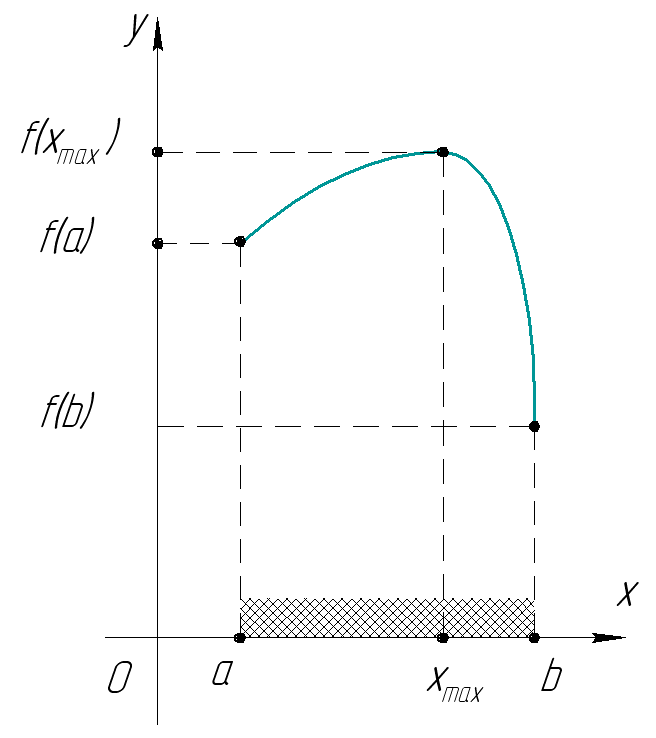
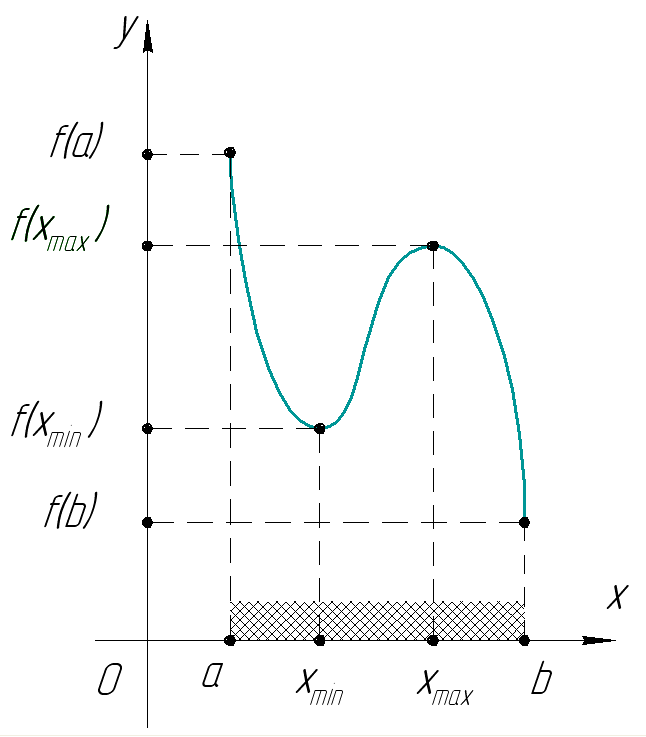
Наибольшее и наименьшее значение функции, непрерывное на отрезке |
|||
Свойства |
|||
Если функция непрерывна на отрезке и имеет на нем конечное число критических точек, то она принимает свое наибольшее и наименьшее значение на этом отрезке или в критических точках, принадлежащих этому отрезку, или на концах отрезка |
|||
Примеры |
|||
|
|
|
|
|
|
|
|
Нахождение наибольшего и наименьшего значения функции, непрерывной на отрезке |
|||
Схема |
Пример Найти наибольшее и наименьше значение функции:
|
||
1. Найти производную
|
|
||
2. Найти критические точки ( |
|
||
3. Выбрать критические точки, принадлежащие заданному отрезку |
Заданному отрезку [1;3] принадлежит только критическая точка х = 2 |
||
4. Вычислить значение функции в критических точках и на концах отрезка |
|
||
5. Сравнить полученные значения и выбрать из них наименьшее и наибольшее |
|
||
АСИМПТОТЫ ГРАФИКА ФУНКЦИИ |
||
Определение. Асимптота кривой – это прямая, к которой неограниченно приближается кривая при удалении ее в бесконечность. |
||
Вертикальные асимптоты (х = а) |
||
асимптота Вертикальная асимптота х = а может быть в точке а, если точка а ограничивает открытие промежутки области при х→а f(x) → ∞ определения данной функции и возле точки а функция уходит в бесконечность |
||
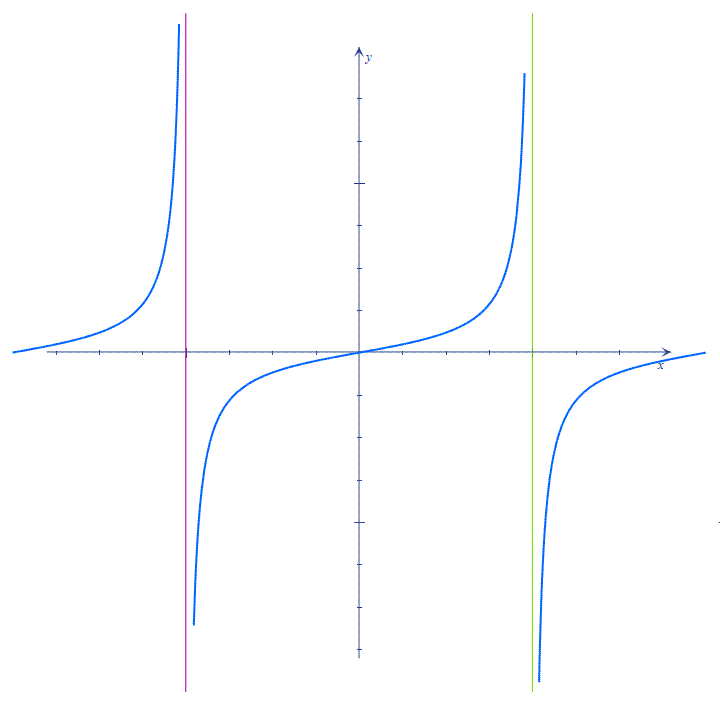
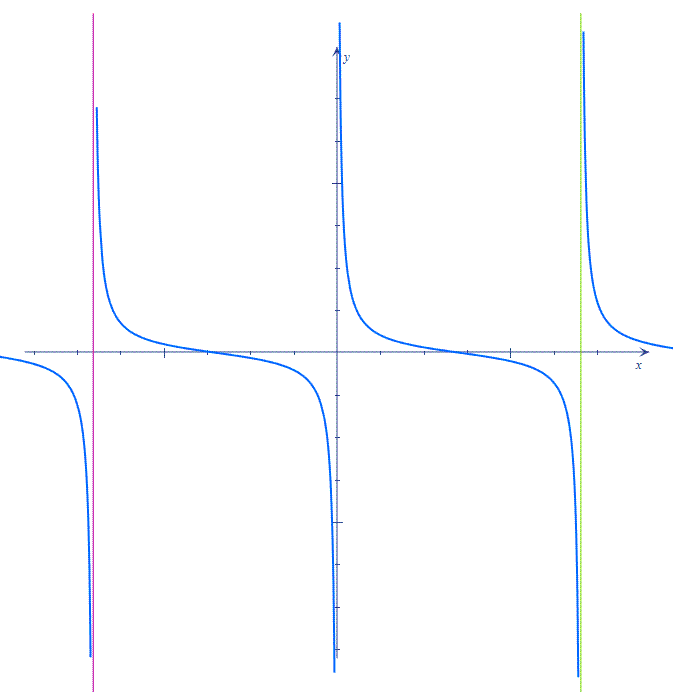
Примеры вертикальных асимптот |
||
|
|
|
О.О.
При х→0 (справа) y→+∞ При х→0 (слева) y→-∞
X = 0 – вертикальная асимптота
|
О.О.
При х→0 (справа) y→-∞
X = 0 – вертикальная асимптота
|
О.О.
При
х→ При х→ (справа) y→-∞ X = - вертикальная асимптота
|
Таблица 5.
Наклонные и горизонтальные асимптоты |
|
1. Если f(x) – дробно-рациональная функция, в которой степень числителя на единицу больше степени знаменателя, то выделяем целую часть и используем определение асимптоты. |
|
Пример 1 |
Пример 2 |
При
|
При
|
|
|
2. В общем случае уравнения наклонных и горизонтальных асимптот y = kx + b могут быть получены с использованием формул: |
|
|
|
Для примера 1 |
Для примера 2 |
|
|
Таблица 6.
ВТОРАЯ ПРОИЗВОДНАЯ И ТОЧКИ ПЕРЕГИБА |
|
Понятие второй производной |
|
|
Пусть функция
|
Пример.
|
|
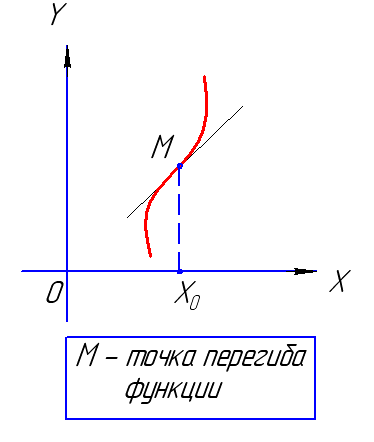
Понятия выпуклости, вогнутости и точек перегиба графика функции |
|
Пусть функция
определена
на промежутке (а; в), а в точке
Тогда
к графику этой функции в точке
|
|
|
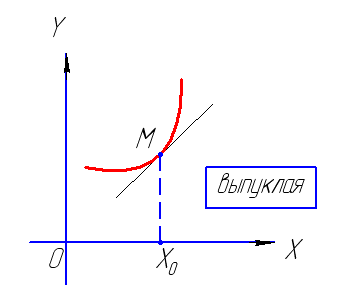
Если в некоторой окрестности точки М все точки кривой графика функции (кроме самой точки М) лежат выше касательной, то говорят, что кривая (и сама функция) в точке М выпуклая (точнее, строго выпуклая). Также иногда говорят, что в этом случае график функции направлен выпуклостью вниз. |
|
Если в некоторой окрестности точки М все точки кривой графика функции (кроме самой точки М) лежат ниже касательной, то говорят, что кривая (и сама функция) в точке М вогнутая (точнее, строго вогнутая). Также иногда говорят, что в этом случае график функции направлен выпуклостью вверх. |
|
Если точка
- точка перегиба функции В
некоторой окрестности точки
:
при
|
Достаточные усовия выпуклости и вогнутости функции, которая
имеет первую и вторую производную при
|
|||
Условие выпуклости |
Условие вогнутости |
||
Если в каждой
точке интервала
|
|
Если в каждой
точке интервала
|
|
Замечание: Эти условия являются только достаточными, но не являются необходимыми.
Например, график
функции
хотя
в точке
|
|
||
Нахождение точек перегиба функции, которая имеет вторую производную на заданном интервале |
|||
Необходимое условие |
Достаточное условие |
||
В точке перегиба функции ее вторая производная равна нулю или не существует |
Если функция имеет первую и вторую производную на интервале и ее вторая производная меняет знак при переходе аргумента через точку , то точка является точкой перегиба функции |
||
Исследование функции на выпуклость, вогнутость и точки перегиба |
|||
Схема |
Пример.
|
||
1. Найти область определения и интервалы, на которых функция непрерывна |
Область определения:
|
||
2. Найти вторую производную |
|
||
3. Найти внутренние
точки области определения, в которых
|
|
||
|
|||
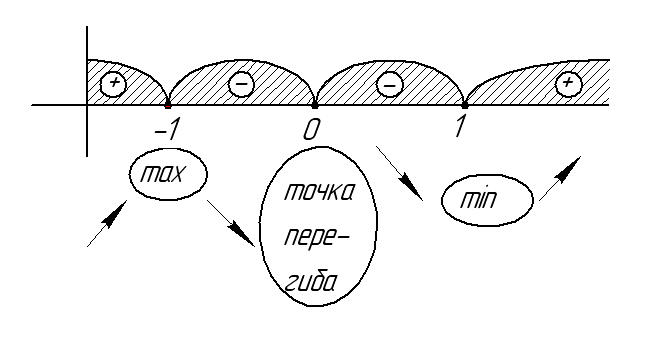
4. Отметить найденные точки на области определения, найти знак производной и характер поведения функции на каждом интервале, на которые разбивается область определения |
|
||
5. Записать требуемый результат исследования (интервалы выпуклости и вогнутости и точки перегиба) |
В интервале
|
||
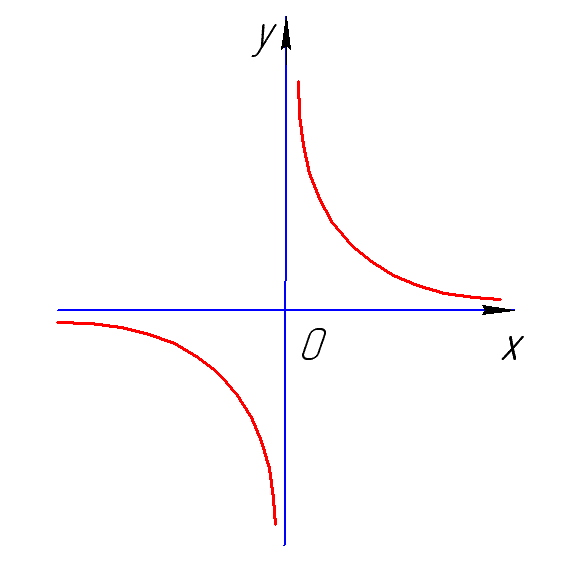
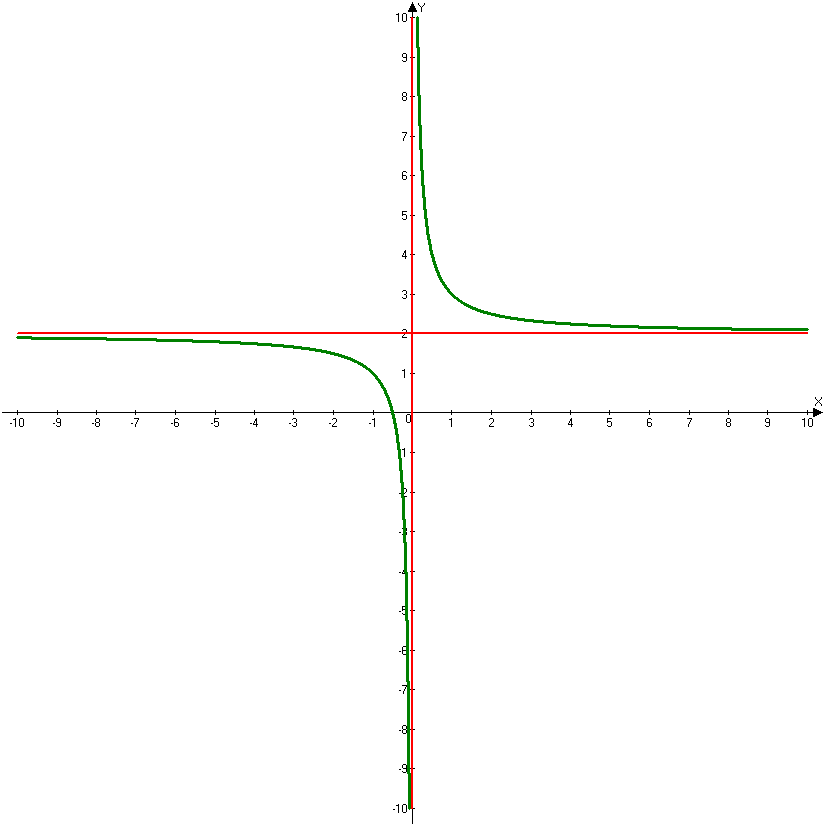
Пример 1:
Исследовать функцию и построить график функции.
1. Область определения функции:
Т.к. знаменатель заданной функции не должен быть равен нулю, то можем записать:
![]()
Функция определена на трех указанных участках.
2.
![]()
Функция четная, график функции симметричен оси OY.
Функция не периодическая.
3. Точки пересечения с осями координат.
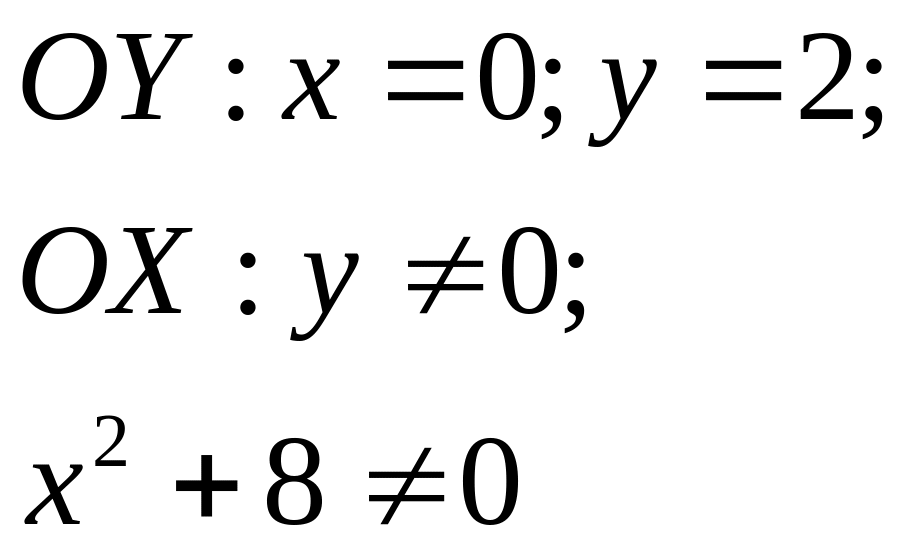
Точка пересечения с осью OY (0;2), точек пересечения с осью OX нет.
4. Производная и критические точки.

5. Промежутки возрастания, убывания, точки экстремума.
На рисунке представлено изменение знака первой производной и поведение функции на участках области определения.
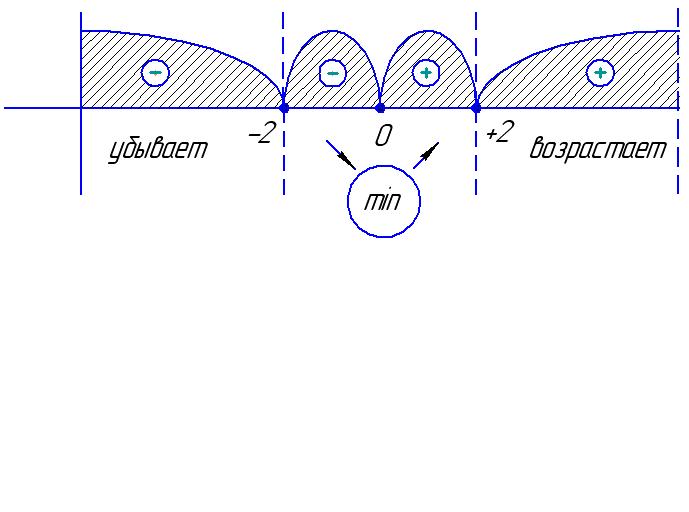
![]()
Точка Х0(0;2) – точка минимума функции.
6. Поведение функции на концах области определения и асимптоты.
При :
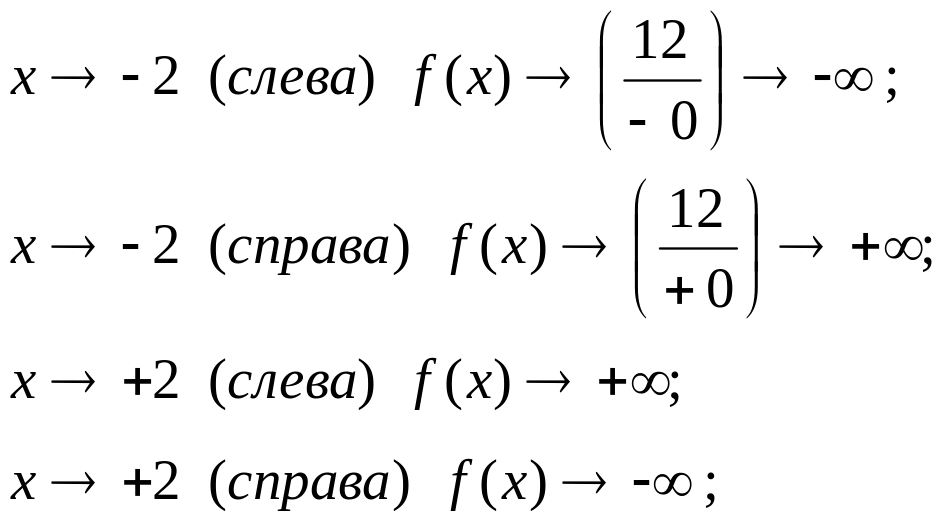
Следовательно, мы
имеем две вертикальные асимптоты
![]()
Наклонные и горизонтальные асимптоты типа: y=kx+b находим по формулам:

Уравнение асимптоты примет вид: y=0*x-1=-1.
Горизонтальная асимптота: Y=-1.
7. Вторая производная и исследование функции на выпуклость и вогнутость.

![]() - не существует в
точках +2 и -2.
- не существует в
точках +2 и -2.
Знак производной меняется в указанных точках.
На рисунке представлено изменение знака второй производной и поведение функции на участках области определения.
![]()
![]()
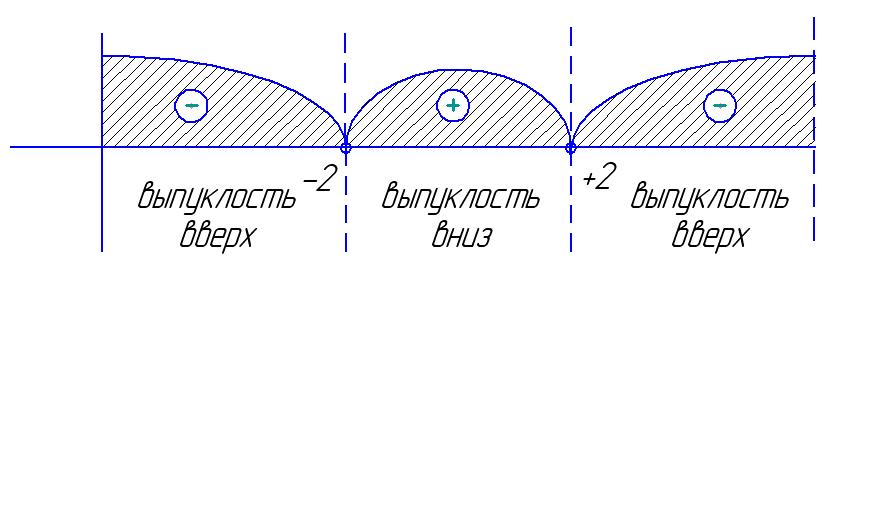
![]()
8. Контрольные точки.
Для более наглядного представления поведения графика функции определим значение функции в точках:

9. График функции представлен на рисунке.
Красным цветом отмечены асимптоты графика и найденные по результатам исследования точки.
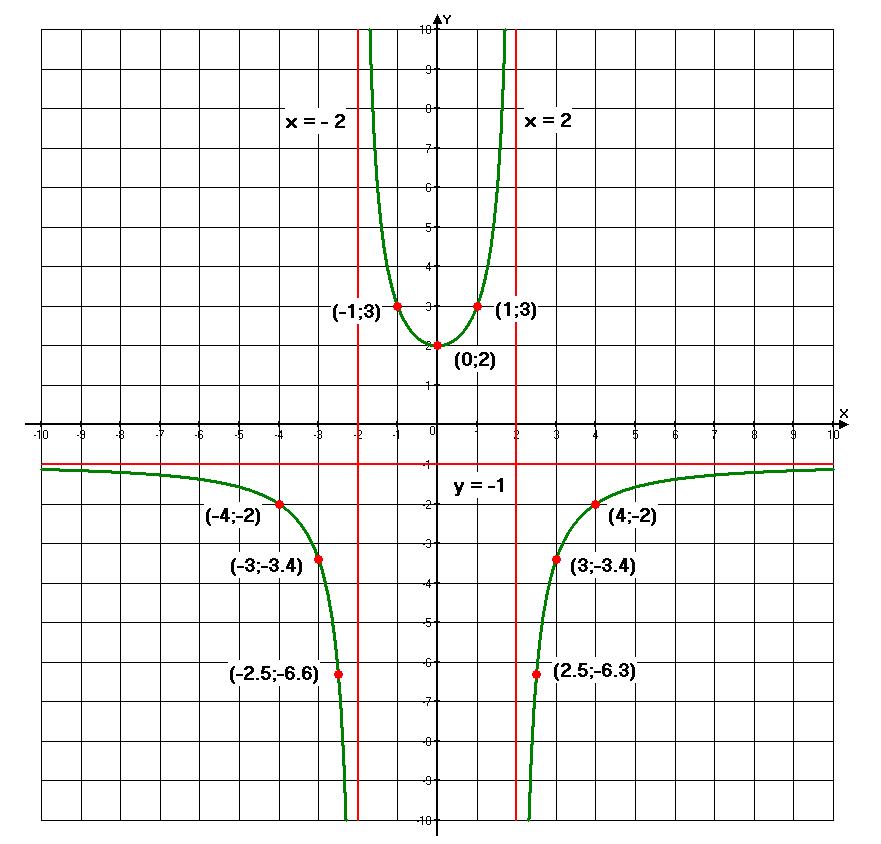
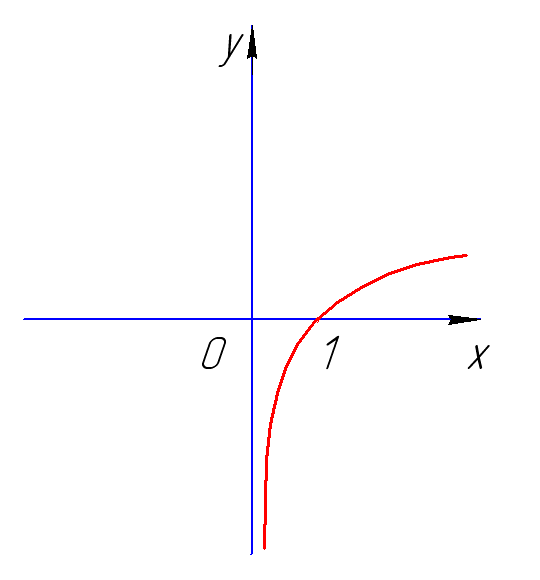
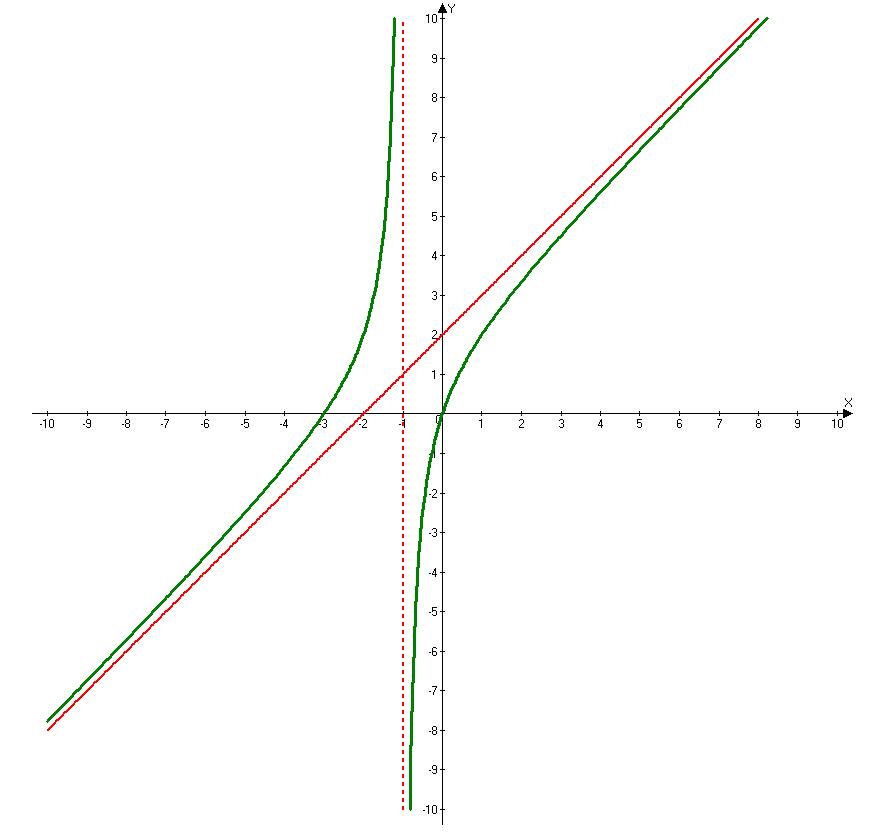
Пример 2:
Исследовать функцию и построить график функции.
1. Область определения функции:
Т.к. под знаком логарифма может стоять только положительное выражение, то можем записать следующее:
![]()
Функция определена на указанном участке.
2.
![]()
Функция ни нечетная, ни четная, не периодическая.
3. Точки пересечения с осями координат.
![]()
Точек пересечения с осью OY нет. Точка пересечения с осью ОХ: х=8.
4. Производная и критические точки.
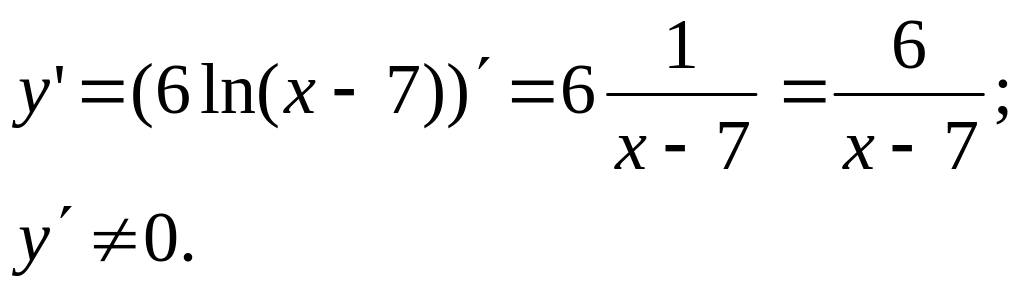
5. Промежутки возрастания, убывания, точки экстремума.
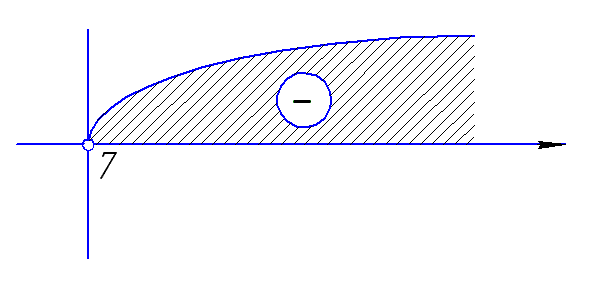
На рисунке представлено изменение знака первой производной и поведение функции на участках области определения.
![]() точек экстремума
нет.
точек экстремума
нет.

возрастает на всей области определения
6. Поведение функции на концах области определения и асимптоты.
При :
![]()
Следовательно, мы
имеем вертикальную асимптоту
![]()
Наклонные и горизонтальные асимптоты типа: y=kx+b находим по формулам:

наклонных и горизонтальных асимптот нет.
7. Вторая производная и исследование функции на выпуклость и вогнутость.

Вторая производная не меняет знак на всей области определения.
выпуклость вверх
8. Контрольные точки.
Для более наглядного представления поведения графика функции определим значение функции в точках:
![]()
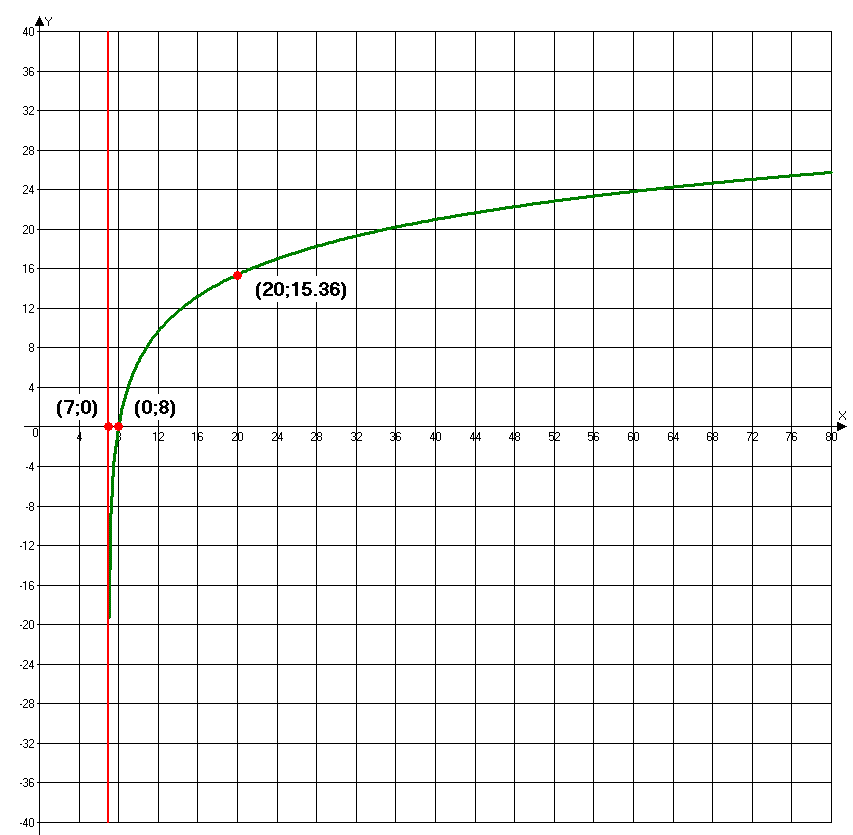
9. График функции представлен на рисунке.
Красным цветом отмечены асимптоты графика и найденные по результатам исследования точи.
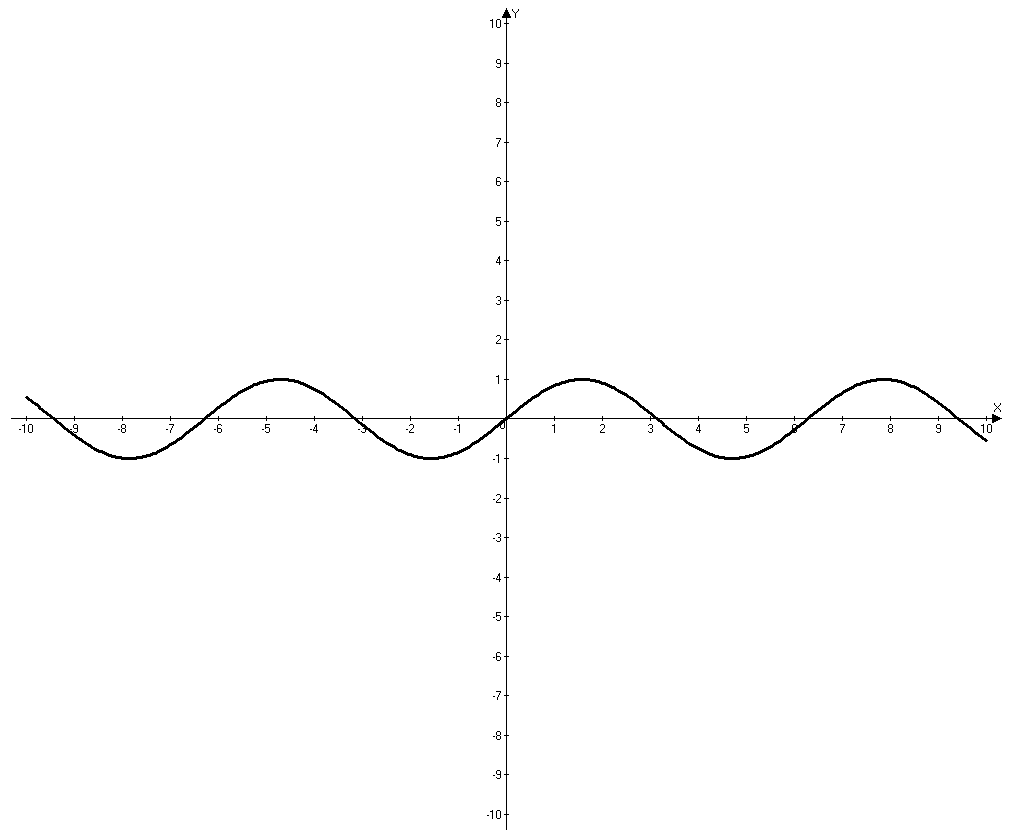
Пример 3:
Исследовать функцию и построить график функции.



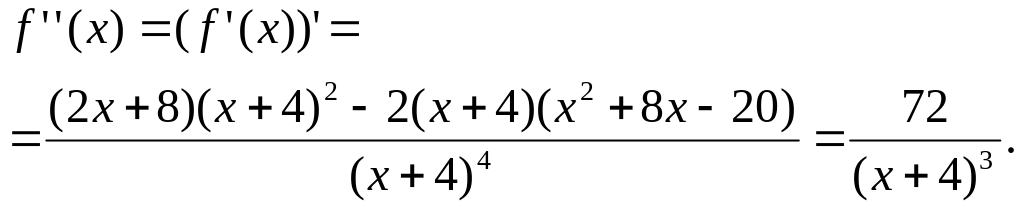
 оскольку
оскольку
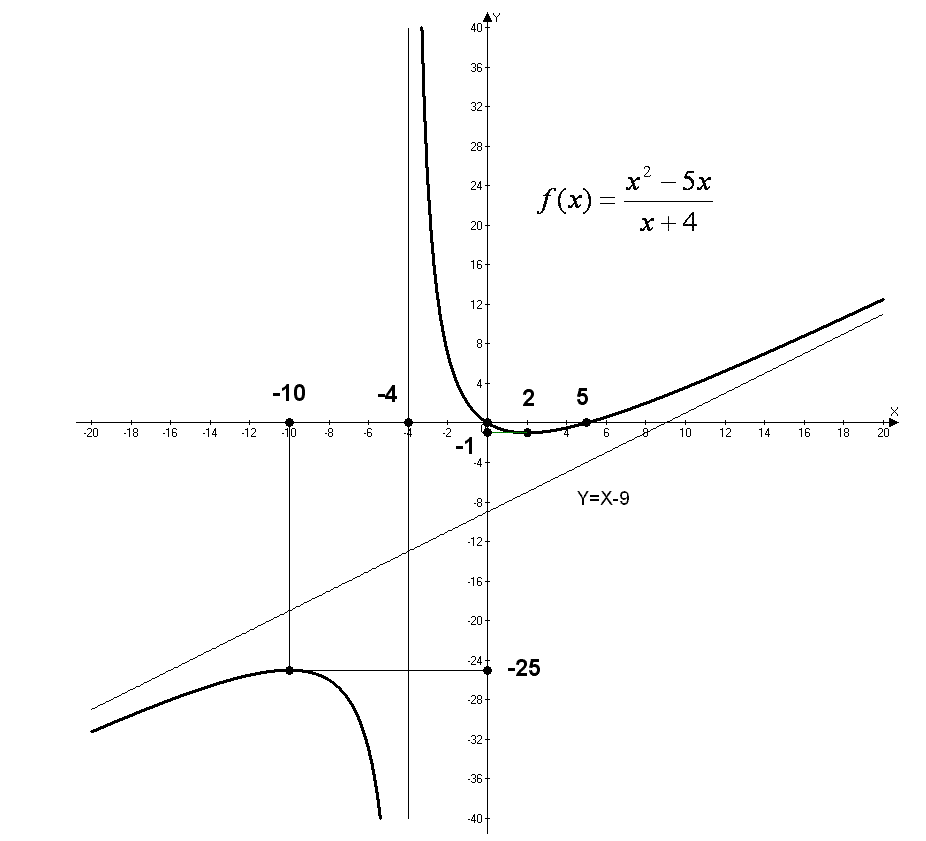



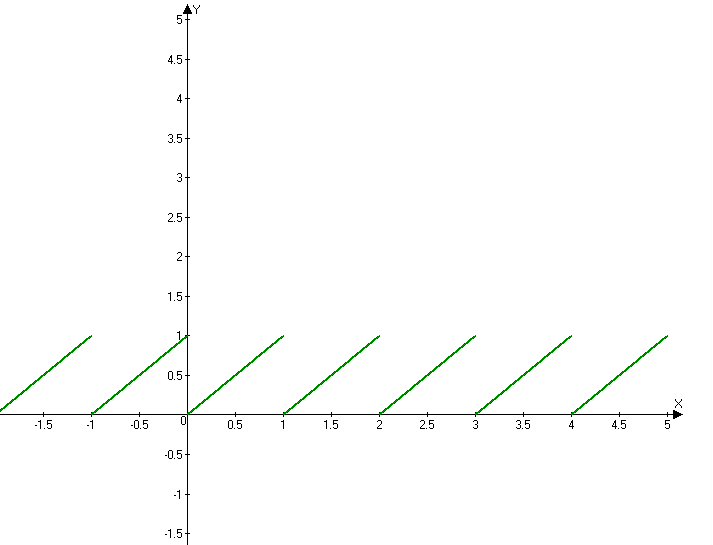
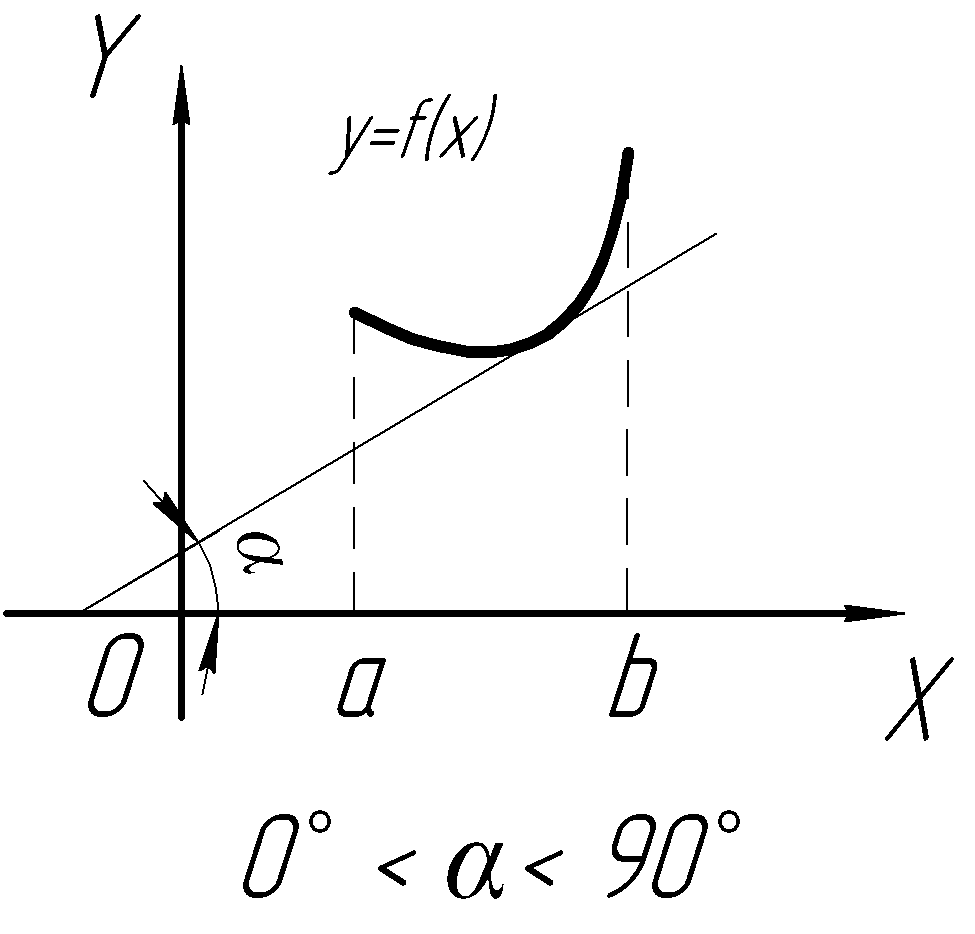
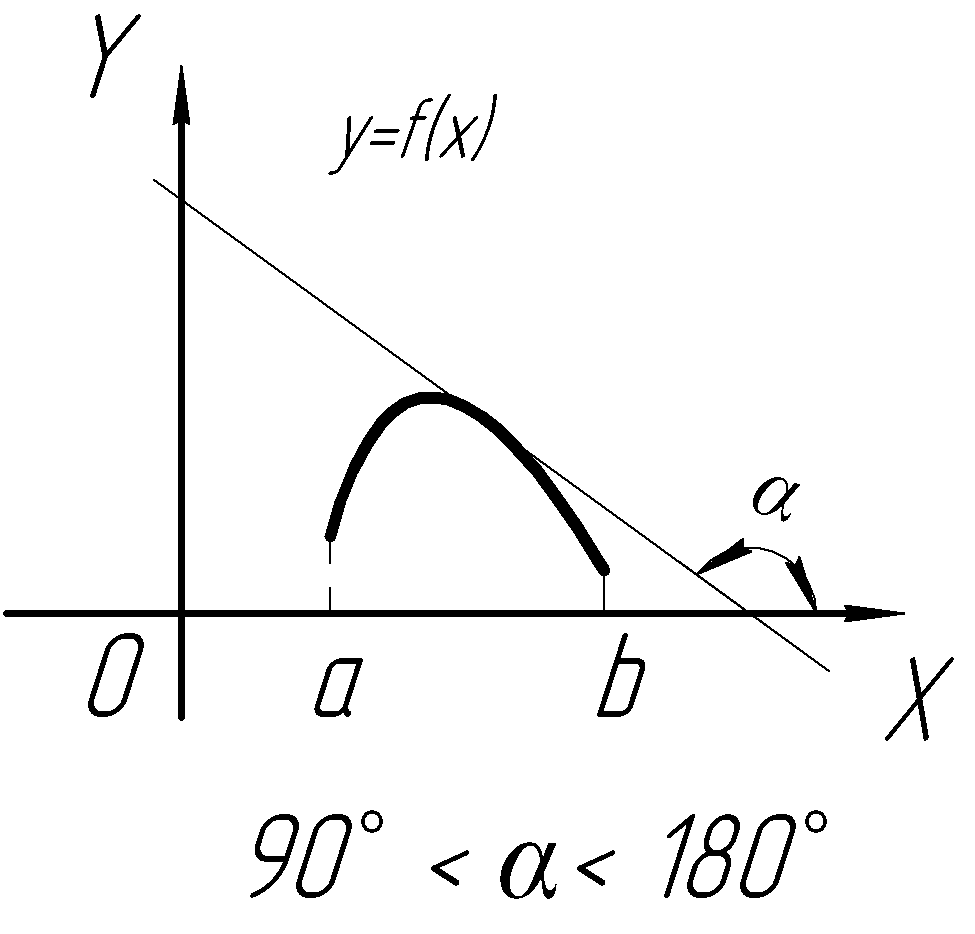
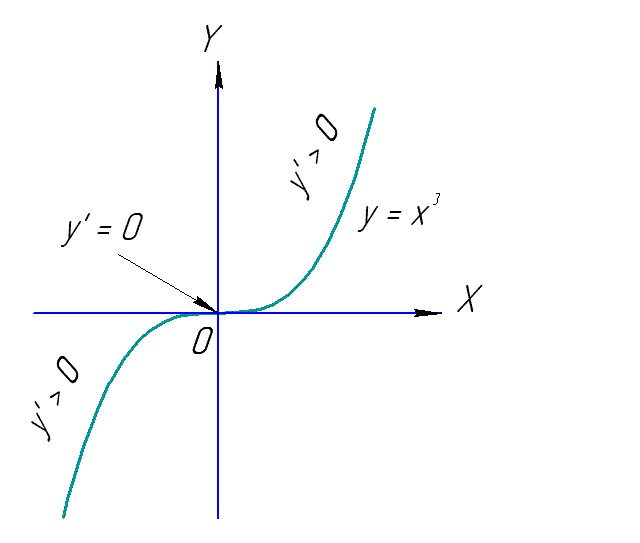 амечание. Эти
условия являются только достаточными,
амечание. Эти
условия являются только достаточными,
 акая,
что для всех
акая,
что для всех
 )
точки
,
такая,
что для всех
из этой окрестности
выполняется
неравенство
)
точки
,
такая,
что для всех
из этой окрестности
выполняется
неравенство