
- •Глава XIV Теория аналитических функций.
- •§79. Функции и функциональные ряды. Элементарные функции.
- •§80. Производная и интеграл.
- •§80. Производная и интеграл (продолжение).
- •§81. Интеграл Коши и его следствия.
- •§ Ряд Лорана и изолированные особые точки однозначных аналитических функций.
- •§83. Вычеты и их приложения.
- •Конформные отображения
Конформные отображения
Дробно-линейное
отображение (окружность в окружности)
представляется 3-мя точками:
![]() тогда
тогда
![]()
разность где встречается ∞ заменяется единицей.
№220. Написать какую-либо дробно-линейную функцию, которая переводит круг
 в
нижнюю полуплоскость.
в
нижнюю полуплоскость.
Решение.
На границе данного круга выберем три точки, например, z1=0, z2=2, z3=-2i. на окружности задается направление обхода, при котором круг оказывается справа.
Выберем теперь в плоскости w на действительной оси (которая является границей нижней полуплоскости) три точки w1, w2, w3 таким образом, чтобы при соответствующем обходе границы нижняя полуплоскость оставалась справа. Можно взять, например, w1=0, w2=1, w3=∞. По выбранным трем парам соответственных точек , используя формулу (7.4), запишем искомую дробно-линейную функцию:
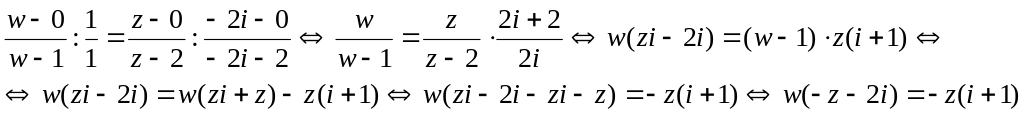
![]() - искомое отображение.
Это не единственное решение, т.к. точки
z1,
z2,
z3,
w1,
w2,
w3
– произвольные.
- искомое отображение.
Это не единственное решение, т.к. точки
z1,
z2,
z3,
w1,
w2,
w3
– произвольные.
Отобразить полосу
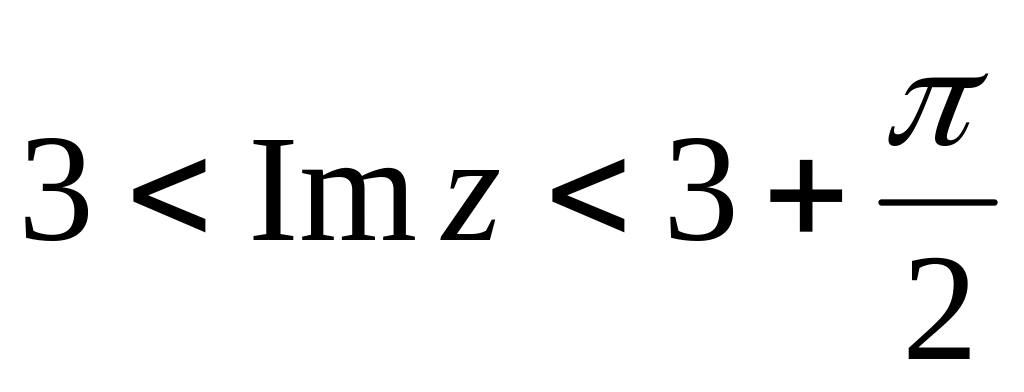 на верхнюю полуплоскость:
на верхнюю полуплоскость:Рассматривая отображение w1=z-3i, получим полосу
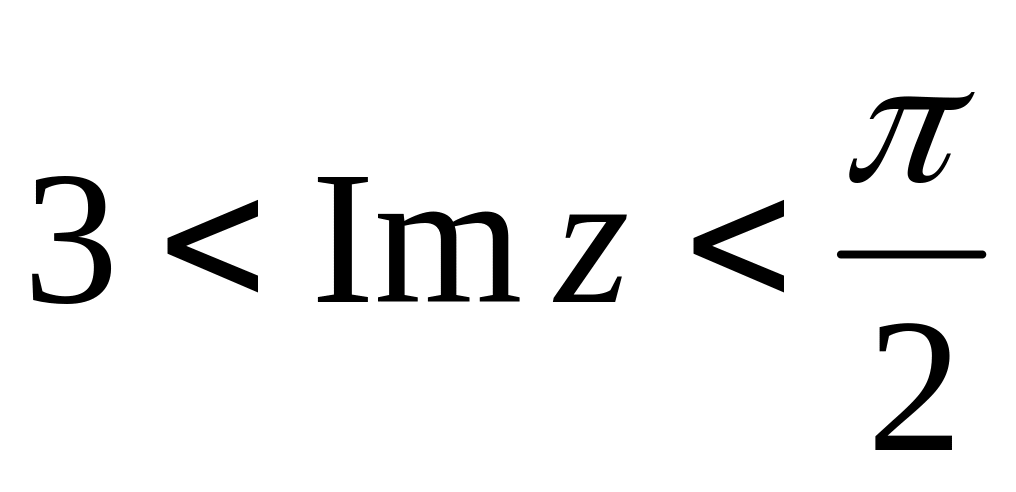
с помощью отображения
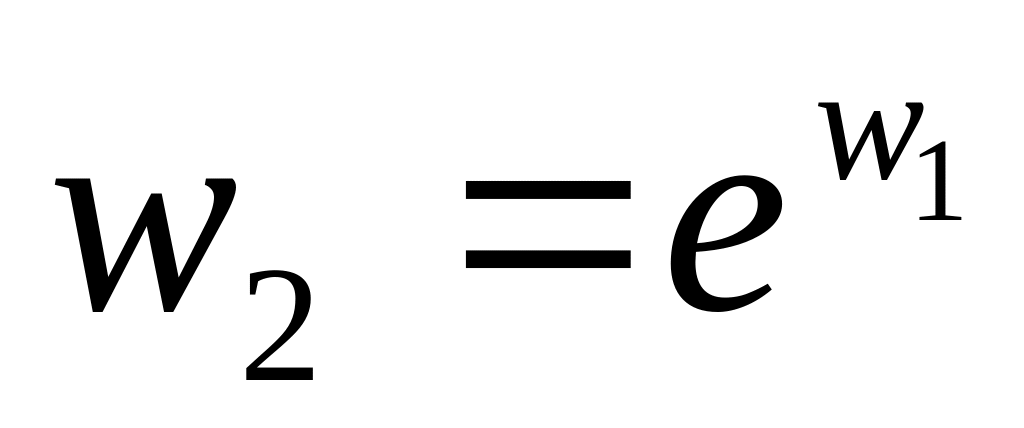 (полоса 0<y<h
(h<2π)
преобразуется в угол раствора h
с вершиной в начале координат)
(полоса 0<y<h
(h<2π)
преобразуется в угол раствора h
с вершиной в начале координат)
![]() преобразует полосу
в
преобразует полосу
в
![]()
наконец, отображение w3=w2 (угол
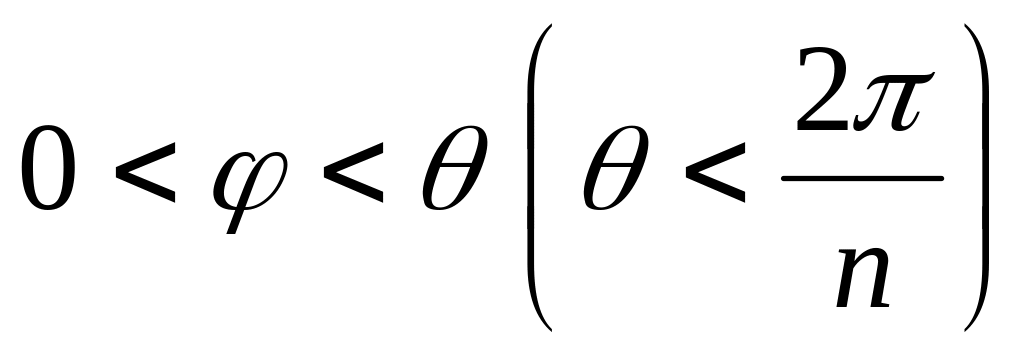 в угол
в угол
 ).
В нашем случае
).
В нашем случае

Найти функцию, отображающую область
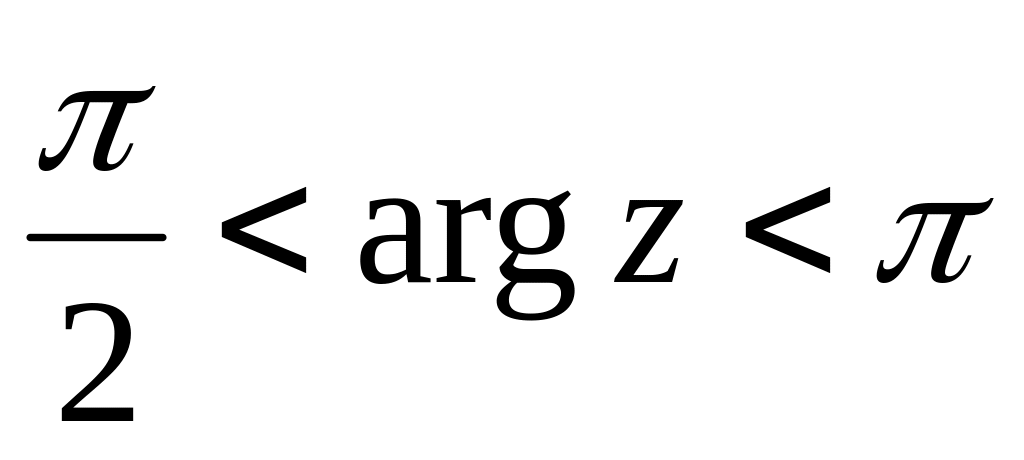 на область
на область
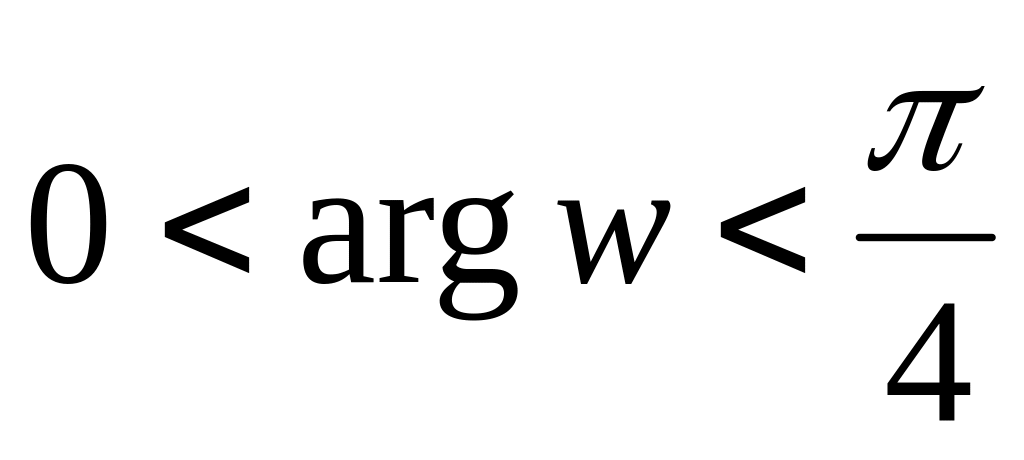 .
.осуществим поворот вокруг нуля на
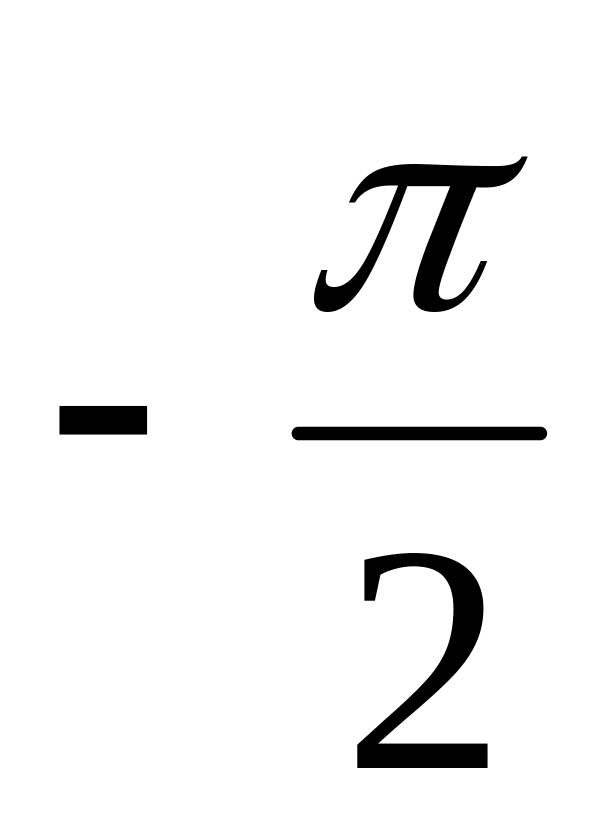 ,
это осуществляет функция
,
это осуществляет функция
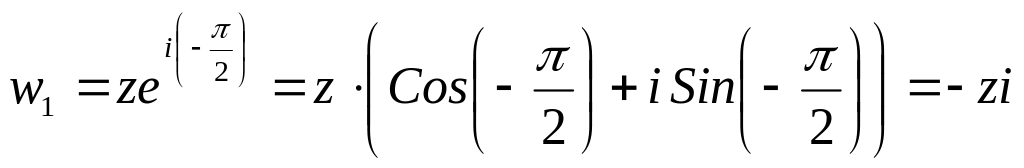
Следовательно,
при данном повороте угол
![]() преобразуется в
преобразуется в
![]() .
.
Рассмотрим отображение
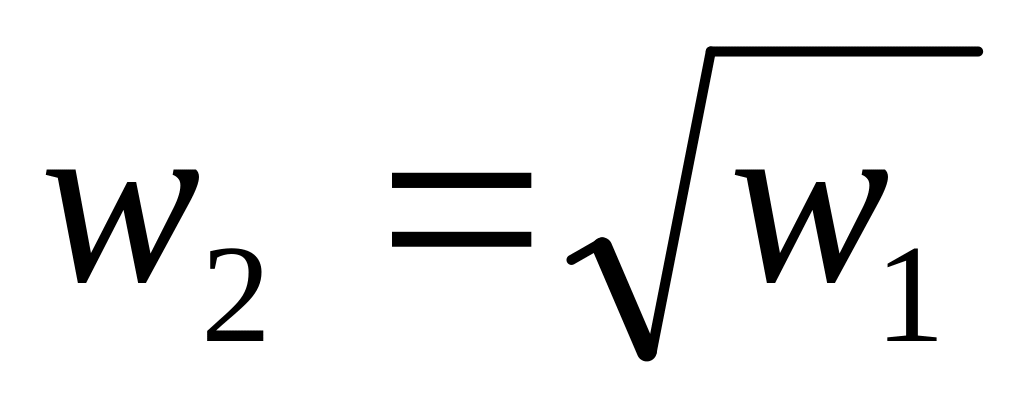 преобразующее угол
преобразующее угол
 в угол
в угол
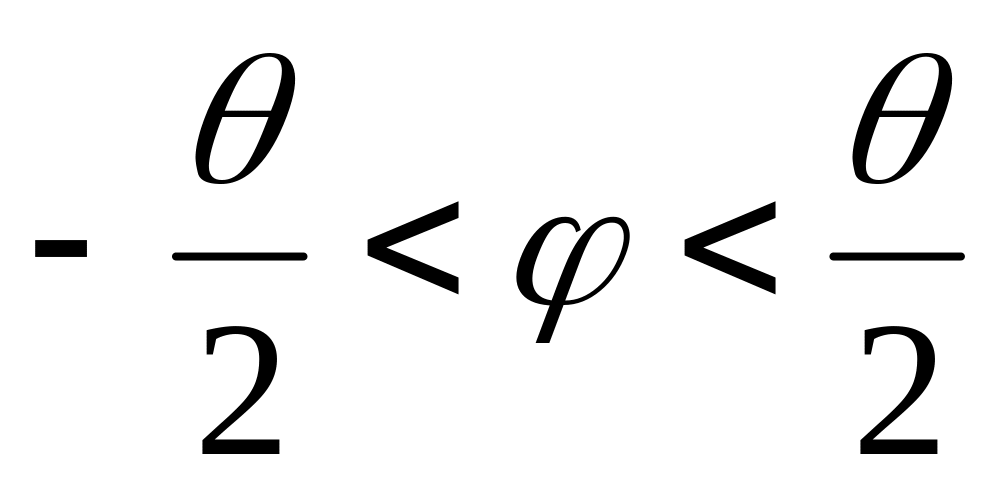 .
В нашем случае
.
В нашем случае
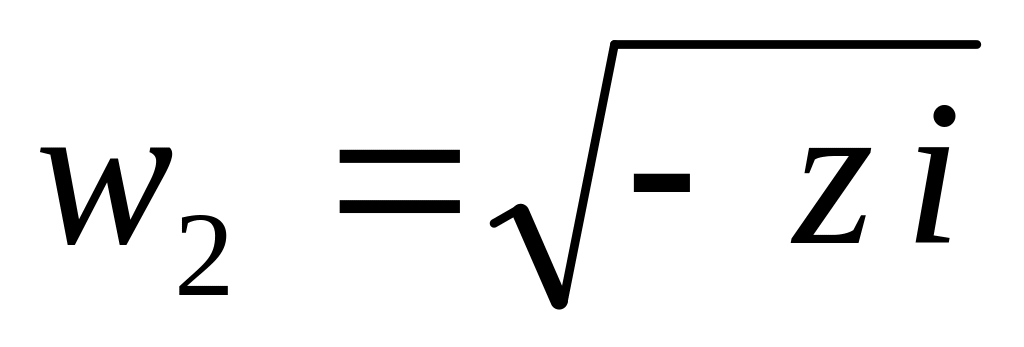
Отобразить угол раствора
 с вершиной в точке z=2+i
ограниченный лучами Arg
(z-2-i)=0+2kπ,
с вершиной в точке z=2+i
ограниченный лучами Arg
(z-2-i)=0+2kπ,
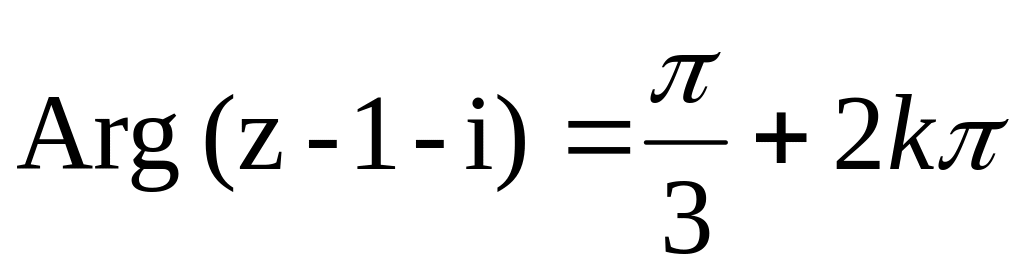 на нижнюю полуплоскость.
на нижнюю полуплоскость.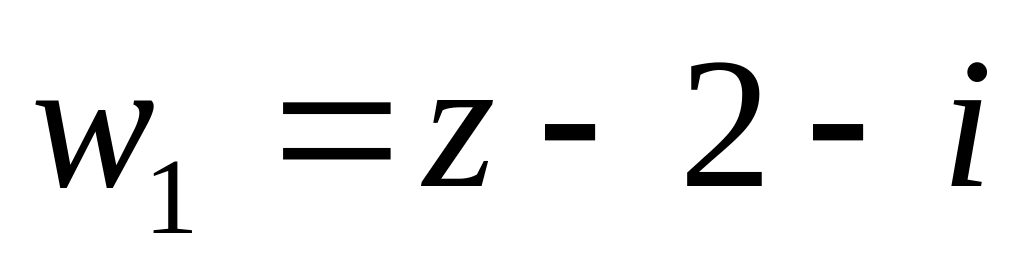 (переводит угол
с вершиной в начале координат)
(переводит угол
с вершиной в начале координат)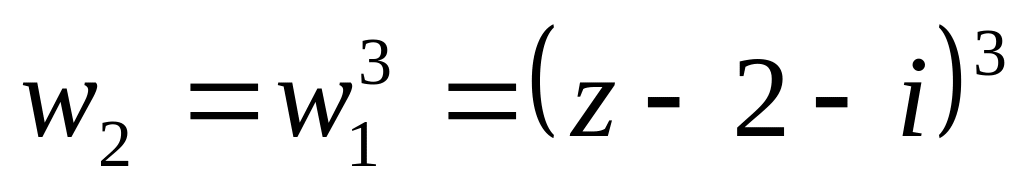 угол в верхней
полуплоскости
угол в верхней
полуплоскости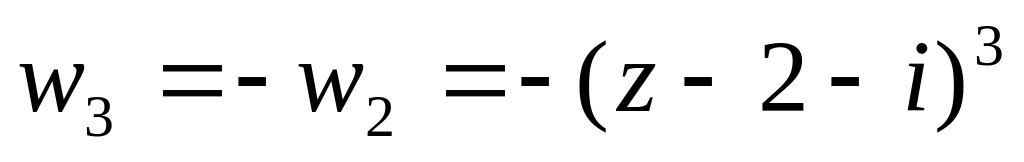 - искомое
отображение.
- искомое
отображение.
