§81. Интеграл Коши и его следствия.

Пусть – аналитическая функция в области D и L – кусочно-гладкий контур , который вместе со своей внутренностью D^* целиком принадлежит D. Тогда для любой точки справедливы равенства:

Пусть – аналитическая функция в области D и точка . Тогда в круге , где R – расстояние от точки z₀ до границы области D, можно представить в виде суммы степенного ряда:

, где

Если функция в круге представляется в виде суммы степенного ряда , то этот ряд единственный и является рядом Тейлора этой функции, т.е. .

Если – аналитическая функция в области D, то в одной точке модуль не может иметь максимума, т.е. не существует такой, что для всех .(принцип максимума модуля)

Функция , имеющая непрерывные частные производные второго порядка в области D и удовлетворяющая в этой области уравнению Лапласа:

,

называется гармонической в D. Две гармонические в области D функции и называются сопряженными, если

для всех точек .

Для наперед заданной гармонической функции в односвязной области D всегда можно построить аналитическую функцию в этой области, действительная часть которой равна . Множество всех таких аналитических функций содержится в формуле :

,

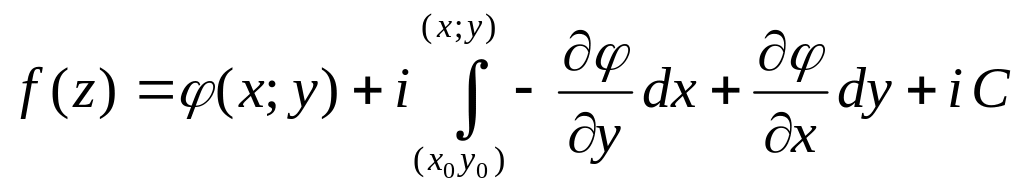где С – действительная постоянная, , , .

§ Ряд Лорана и изолированные особые точки однозначных аналитических функций.

Функция , аналитическая в кольце разлагается в этом кольце в ряд Лорана:

,

причем этот ряд единственный и его коэффициенты a_n определяются по формуле:

,

где Гр – окружность .

Если – однозначная аналитическая функция в области , то в этой области она представляется в виде суммы ряда Лорана:

.

Пусть – аналитическая в области . В этой области ее можно представить в виде суммы ряда Лорана:

.

При этом изолированная особая точка z₀ функции называется:

а) устранимой, если в разложении коэффициенты a_n=0, n = -1; -2;…

б) полюсом порядка , если в этом разложении коэффициенты для n=-(m+1);-(m+2);…, причем полюс называется простым, если m=1 и кратным, если m>1.

в) существенно особой точкой если среди коэффициентов a_n (n = -1; -2;…) содержится бесконечное множество коэффициентов, отличных от нуля.

Если – однозначная аналитическая функция в области , то в этой области она представляется в виде суммы ряда Лорана:

.

Бесконечно удаленная точка при этом называется бесконечно удаленной изолированной особой точкой функции . Эта точка называется:

а) устранимой особой точкой, если в разложении коэффициенты a_n=0 для n =1;2;…

б) полюсом порядка , если , причем полюс называется простым, если m=1 и кратным, если m>1.

в) существенно особой точкой, если среди коэффициентов a_n (n =1; 2;…) содержится бесконечное множество коэффициентов, отличных от нуля.

Для того чтобы изолированная особая точка z₀, конечная или бесконечно удаленная, аналитической функции была устранимой (полюсом), необходимо и достаточно, чтобы существовал конечный (бесконечный) предел рассматриваемой функции в этой точке.

Если в достаточно малой окрестности изолированной особой точки z₀ конечной или бесконечно удаленной, однозначная аналитическая функция ограничена, то z_0­ – устранимая особая точка функции .

Если z_0­ – существенно особая точка, конечная или бесконечно удаленная, однозначной аналитической функции , то для любого комплексного числа А, конечного или бесконечно удаленного, существует последовательность точек z_n , , такая что .

В задачах 2830-2851 найти изолированные особые точки аналитической функции и выяснить их характер.

№2830.

Решение

Очевидно, особые точки содержатся среди, тех при которых знаменатель обращается в нуль и в ∞.

Отсюда, .

Т.к. ,

то - простые полюса,

а ∞ - устранимая особая точка.

№2831

Решение

Очевидно, - простые полюсы.

Т.к. ,

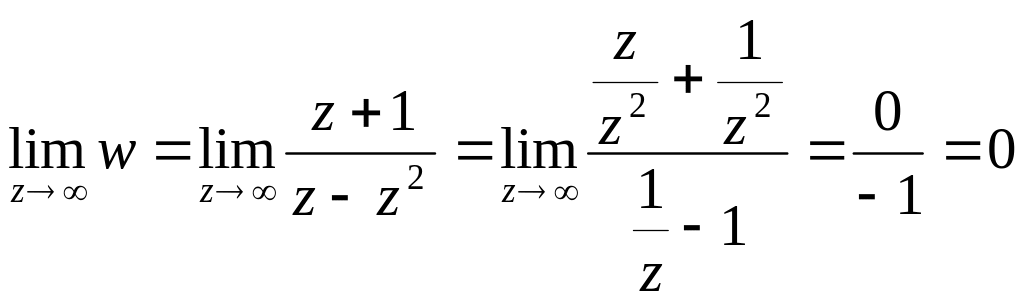то ∞ - устранимая особая точка.

Функция называется аналитической в точке z₀, если она дифференцируема в каждой точке некоторой окрестности точки z₀.

№2832

Решение

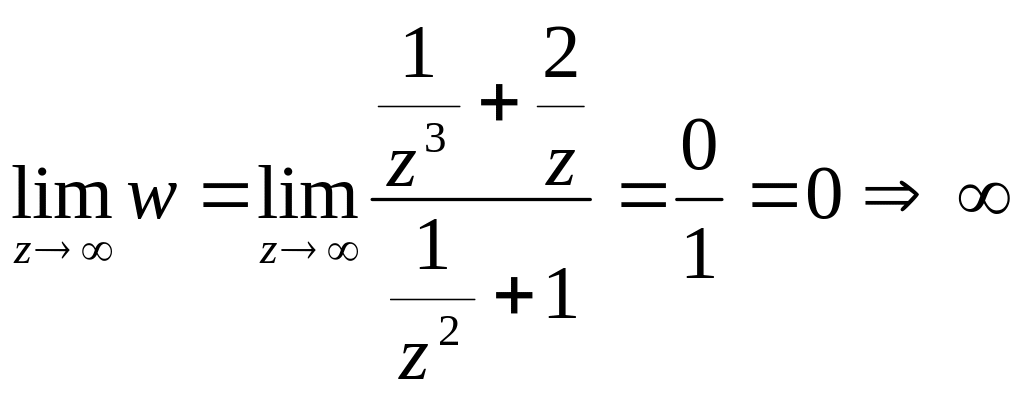- устранимая особая точка.

Т.к. , причем

,

то – простые полюсы.

№2833.

Решение.

– простой полюс.

– полюс второй кратности.

№2834.

Решение.

– устранимая особая точка.

полюс третьей кратности.

№2835.

Решение.

– устранимая особая точка.

– простой полюс, – полюсы второй кратности.

№2836.

Решение

– устранимая особая точка.

– не существует, т.к. не существует ∞ - существенно особая точка.

№2837.

Решение.

– устранимая особая точка.

– не существует, т.к. не существует пределов при и при .

Поэтому, ∞ - существенно особая точка.

№2838.

Решение

Нет конечных особых точек.

– не существует, следовательно ∞ - существенно особая точка.

№2839.

Решение

– устранимая особая точка.

не существует, следовательно ∞ - существенно особая точка.

№2840.

Решение

– полюс третьей кратности

не существует, следовательно ∞ - существенно особая точка.

№2842.

Решение

Нет конечных особых точек.

не существует, следовательно ∞ - существенно особая точка.

№2843.

Решение

∞ – полюс третьей кратности.

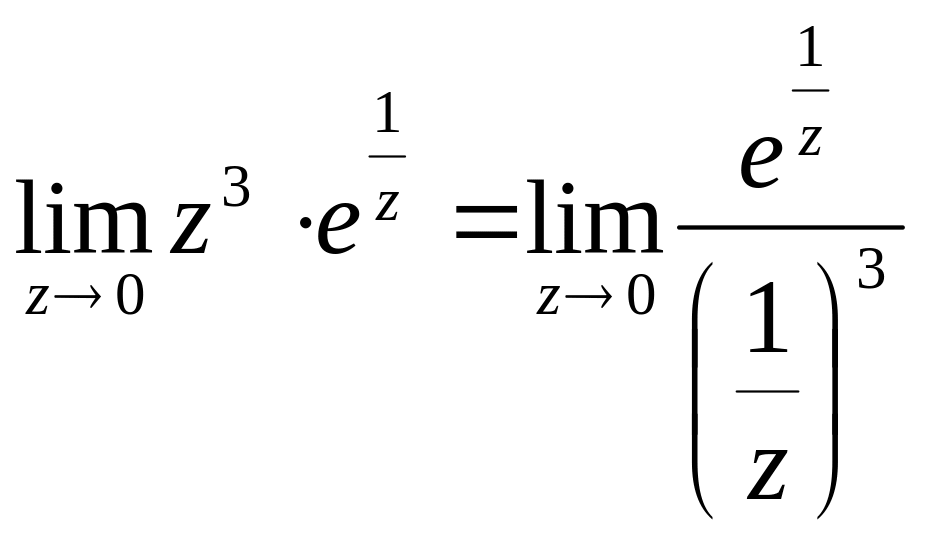не существует, следовательно z=0 - существенно особая точка (см. №2838, 2837, 2842).

№2844.

Решение

– простые полюсы.

не существует, следовательно ∞ - существенно особая точка.

№2845.

Решение

z=1

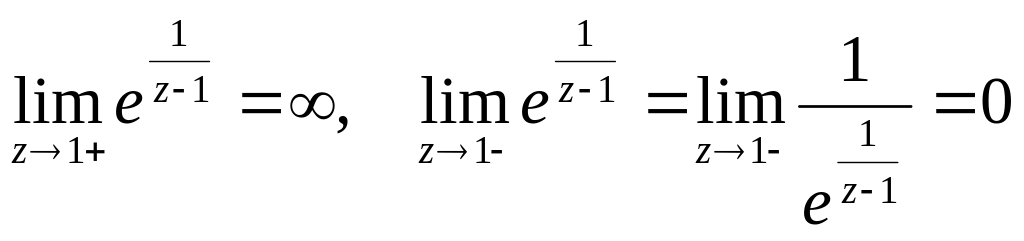
Нет предела в точке z=1, следовательно z=1 - существенно особая точка.

∞ - устранимая особая точка.

№2846.

Решение

z=1

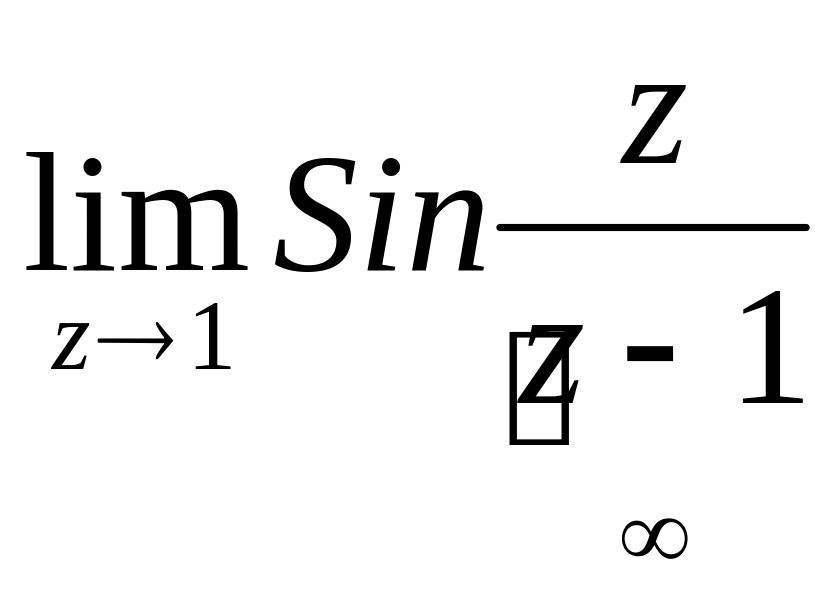не существует, следовательно z=1 – существенно особая точка.

- устранимая особая точка.

№2847.

Решение

z=2

не существует, следовательно z=2 – существенно особая точка.

∞ - устранимая особая точка.

№2848.

Решение

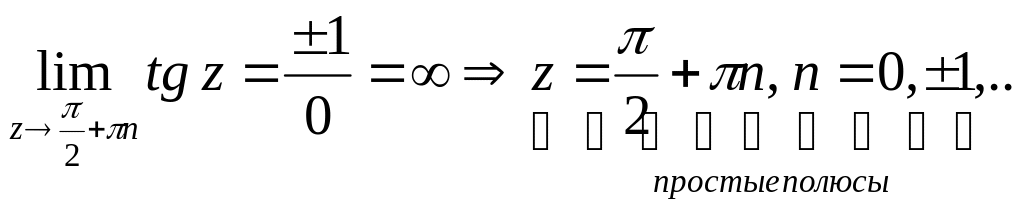
Т.к. эти точки нельзя заключать в круг радиуса R, то ∞ не является изолированной особенностью.

№2849.

Решение

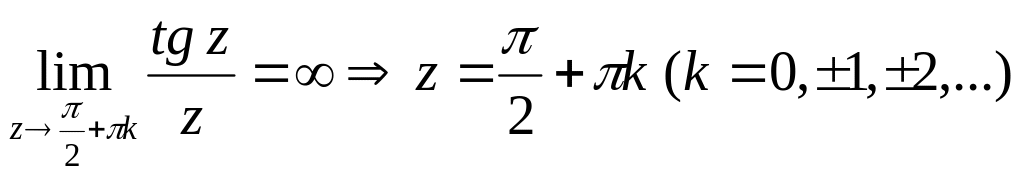- простые полюсы.

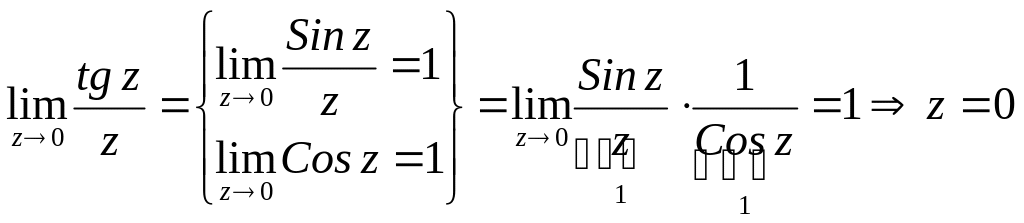- устранимая особая точка.

№2850.

Решение

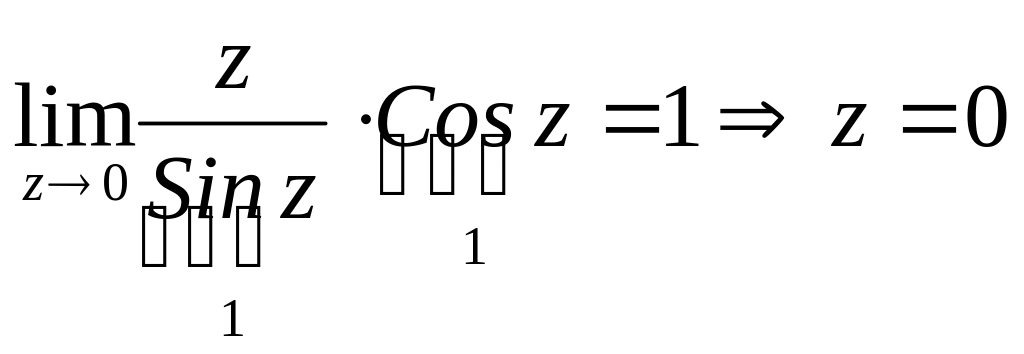- устранимая особая точка.

- простые полюсы.

№2851.

Решение

- полюс второй кратности.

- простые полюсы.

Точка z₀ называется нулём кратности m аналитической функции , если в окрестности этой точки представляется в виде степенного ряда

,

где , причем нуль называется простым, если m=1, и кратным, если m>1.