§80. Производная и интеграл.

Для того чтобы функция была дифференцируема в точке необходимо и достаточно чтобы функции u(x,y) и v(x,y), рассматриваемые как действительные функции от двух действительных переменных x и y, были дифференцируемы в точке (x_­,y) и чтобы имели место равенства:

(условие Коши-Римана) При этом производная может быть вычислена по формулам:

№2756. Проверить выполнение условий Коши-Римана и найти производную функции в следующих задачах. (2756-2759)

w=z². Пусть z=x+iy, тогда w=( x+iy)²=x²-y²+2xyi= , где u(x;y)=x²-y², v(x;y)=2xy.

Проверим условие Коши-Римана:

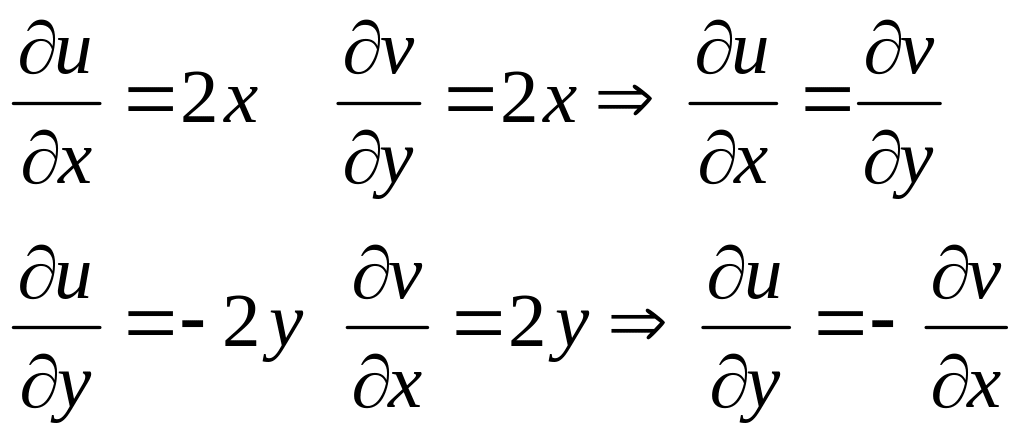т.е. условие Коши-Римана выполняется

№2757.

w=z²+2z-1

Пусть z=x+iy, тогда w=x²-y²+2xyi+2x+2yi-1=x²-y²+2x-1+(2xy+2y)i=u(x;y)+iv(x;y)

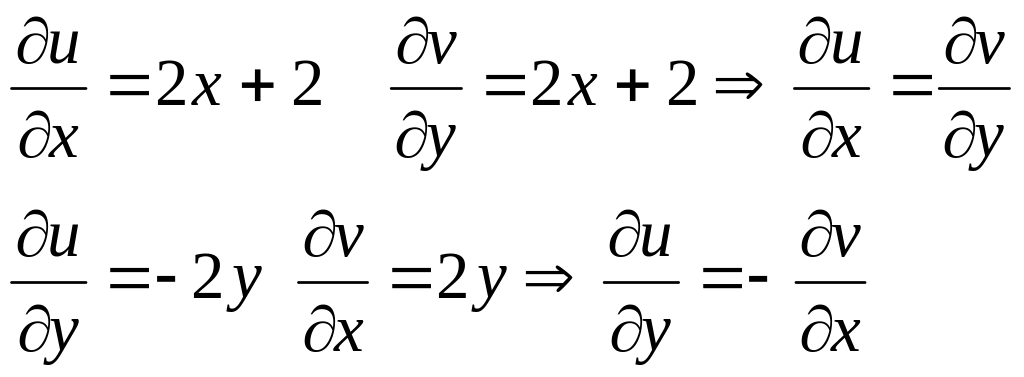т.е. условие Коши-Римана выполняется

№2758.

w=cos 2z

Пусть z=x+iy, тогда

Итак,

Поэтому

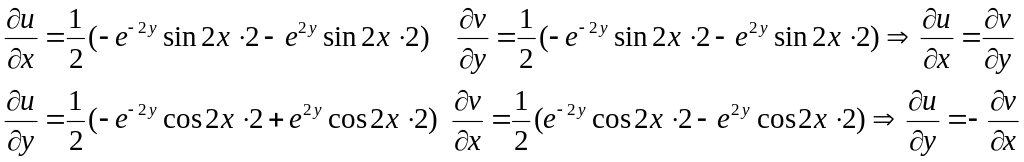
Условие Коши-Римана выполняется.

w´=-2sin 2z

№2761. Доказать, что w=z Im z дифференцируема только в точке z=0, найти w´(0).

Проверим условие Коши-Римана.

Пусть z=x+iy, тогда Im z=y и

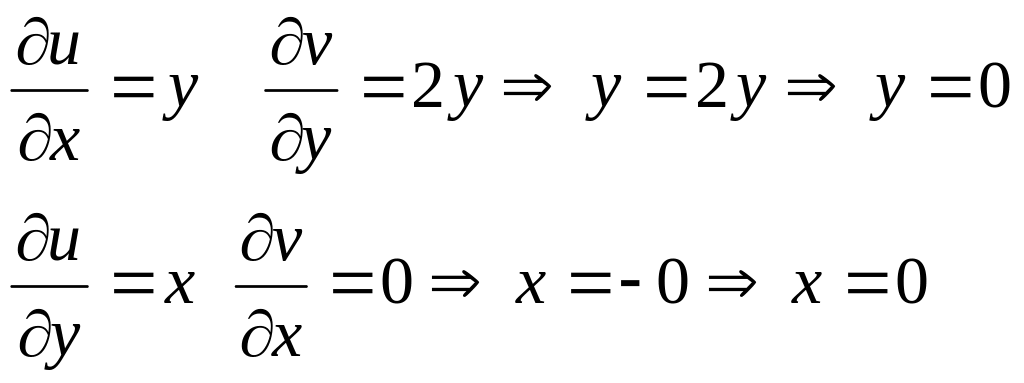
w´(0)=0+i 0=0

№2760. Доказать, что функция нигде не дифференцируема.

Пусть z=x+iy, тогда и

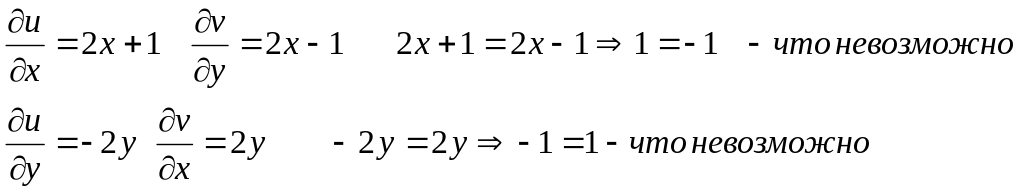
Условие Коши-Римана не выполняется ни в одной точке, следовательно функция нигде не дифференцируема.

§79.

Радиус R сходимости степенного ряда определяется по формуле Коши-Адамара (круг сходимости |z-z₀|<R): 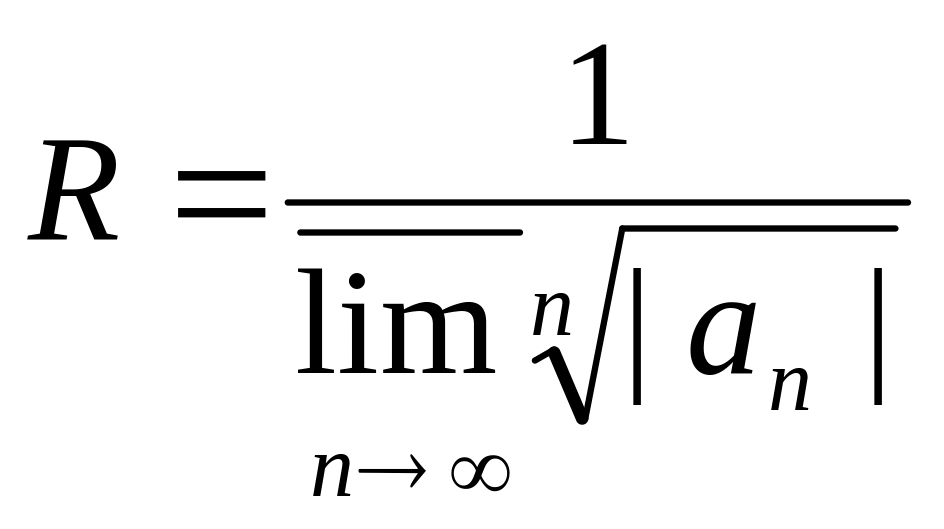, причем R=0, если и R=0, если .

Можно по формуле:

В задачах 2729-2736 определить радиусы сходимости и круг сходимости степенных рядов.

№2729.

(очевидно z₀=0)

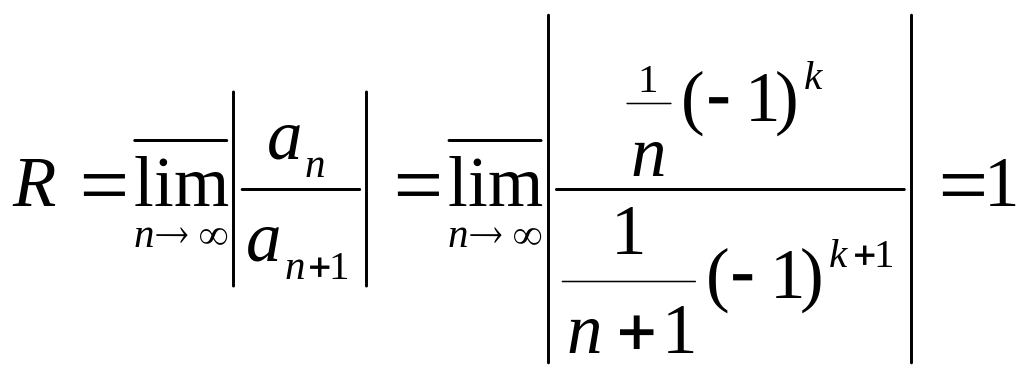
|Z|<1

№2730

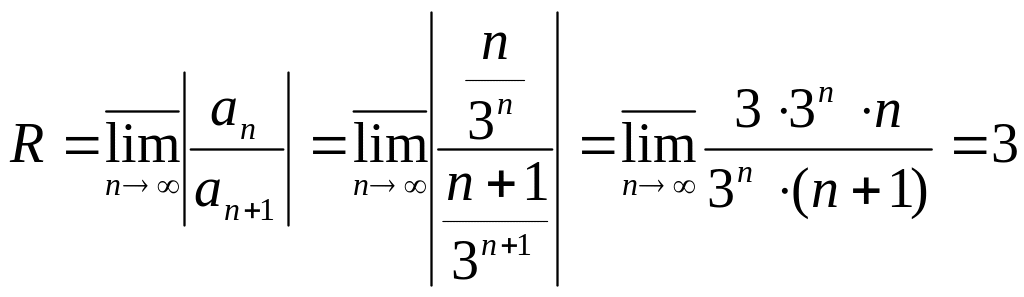, |z-i|<3 - круг сходимости

№2731

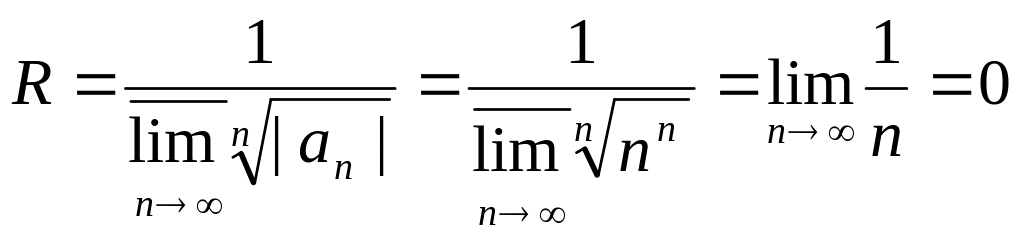
№2732

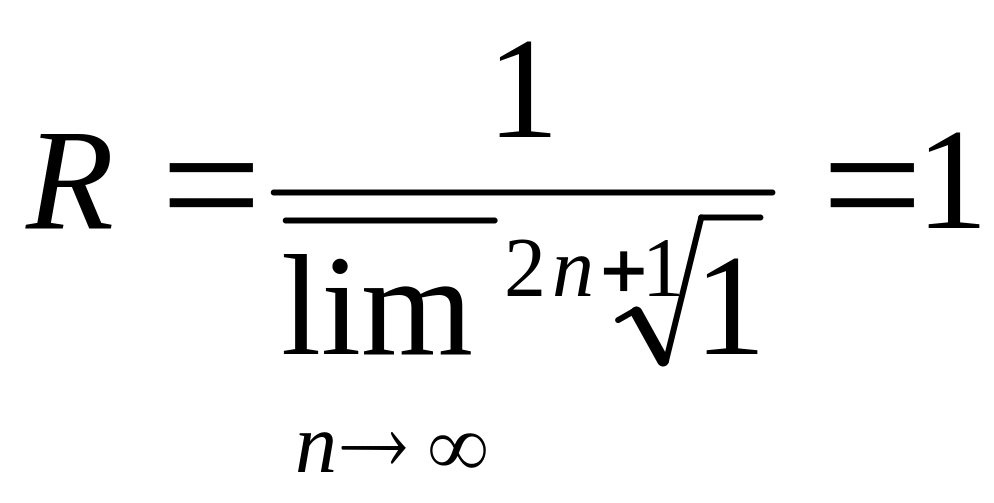
|z-(-1)|<1 (круг сходимости)

№2733

R=1, |z|<1 (круг сходимости)

т.к.

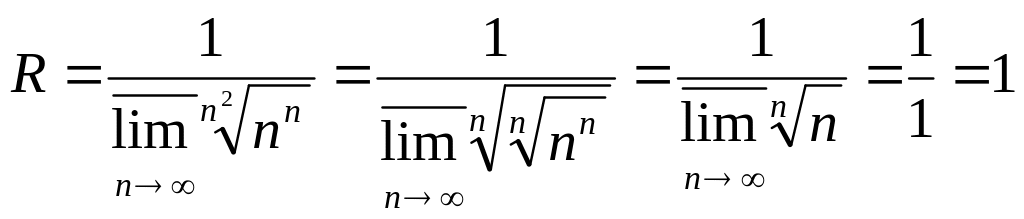
№2734

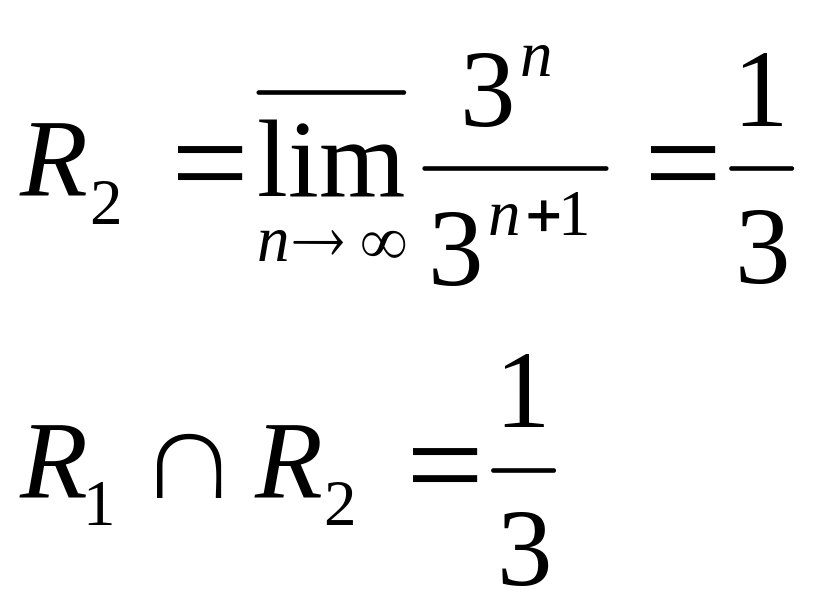
(круг сходимости)

№2735

- круг сходимости

№2735

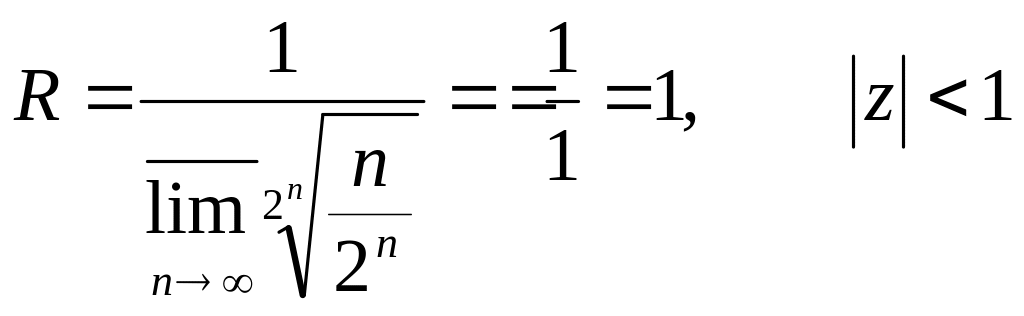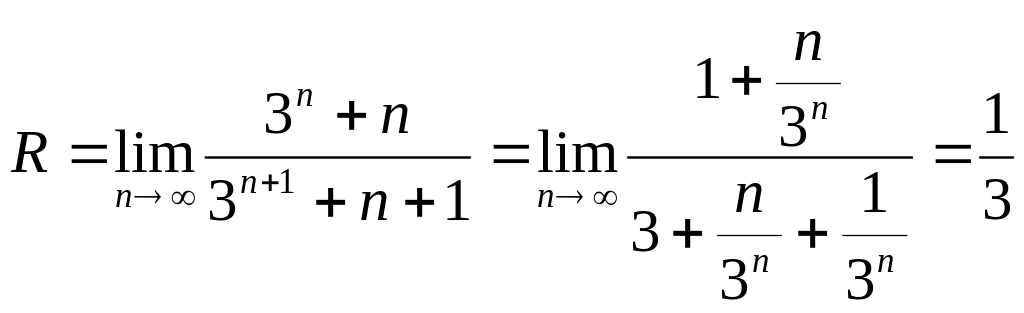
- круг сходимости

§80. Производная и интеграл (продолжение).

Если степенной ряд имеет радиус сходимости R>0, то его сумма дифференцируема в круге |z-z₀|<R, причем

Если функция непрерывна на кусочно-гладкой дуге AB, то:

, где в правой части стоят криволинейные интегралы.

Если уравнение кусочно-гладкой дуги AB записать в виде , то:

, где

№2770. Вычислить интеграл по следующим путям:

1) по отрезку прямой, соединяющему начало координат с точкой z=3+2i;

Решение

Очевидно, . Пусть z=x+iy, тогда , dz=dx+idy; и

2) по полуокружности от точки до точки .

Решение

, следовательно, и есть уравнение нашей полуокружности, т.к. она расположена в верхней полуплоскости. x изменяется от 1 до –1.

Итак, возьмем , , , .

Итак,

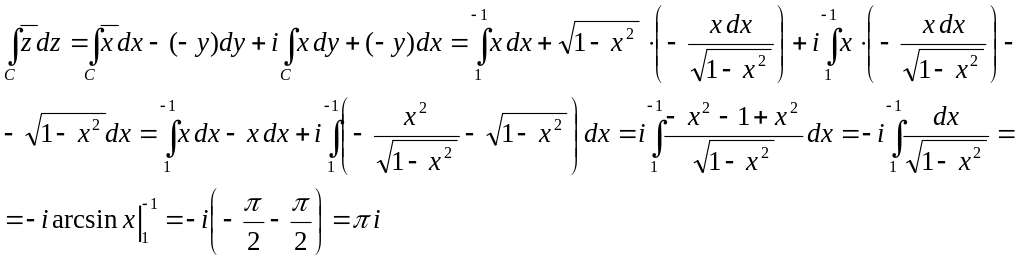
3) По окружности в положительном направлении.

Решение

, ,

.

№2771. Вычислить интеграл по следующим путям:

1. По отрезку прямой, соединяющему начало координат с точкой .

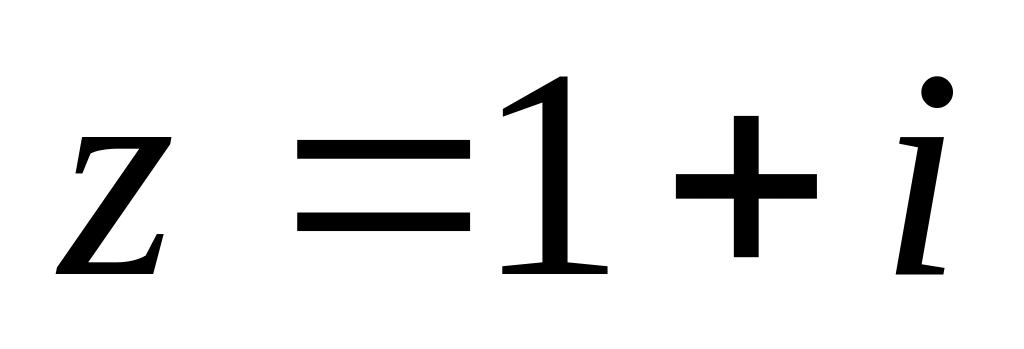Решение

Уравнение прямой: .

.

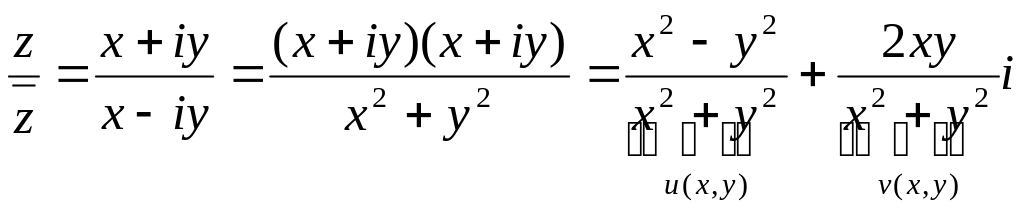
Тогда,

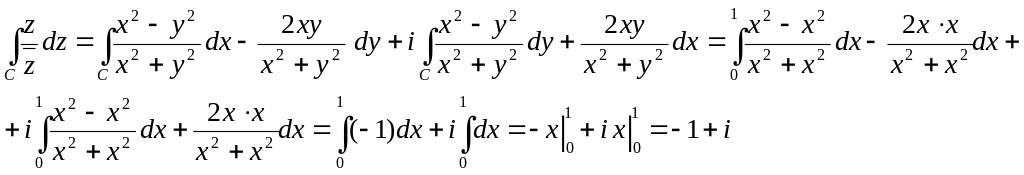
2. По дуге параболы 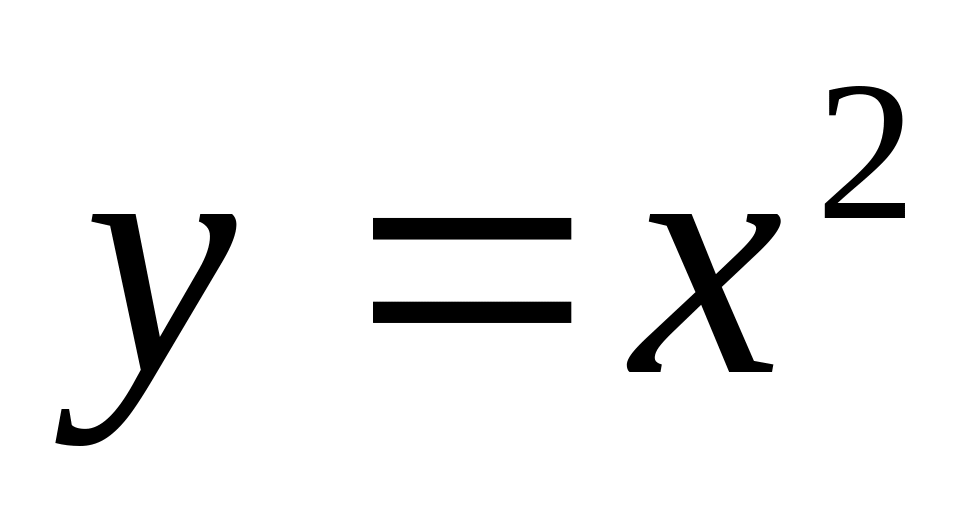от точки до точки .

Решение

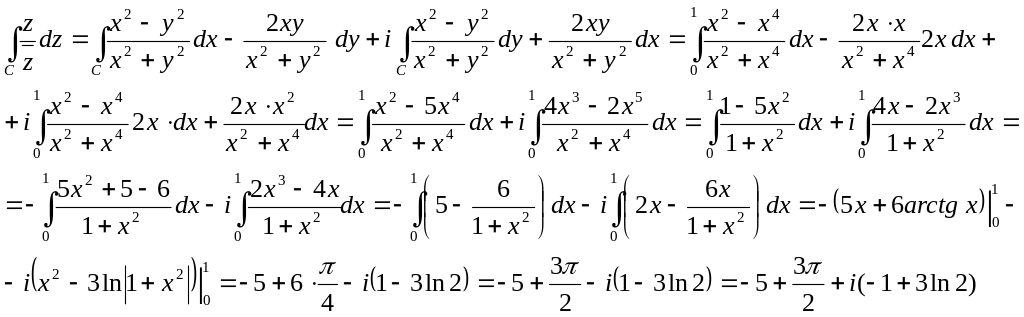
3. По дуге кривой 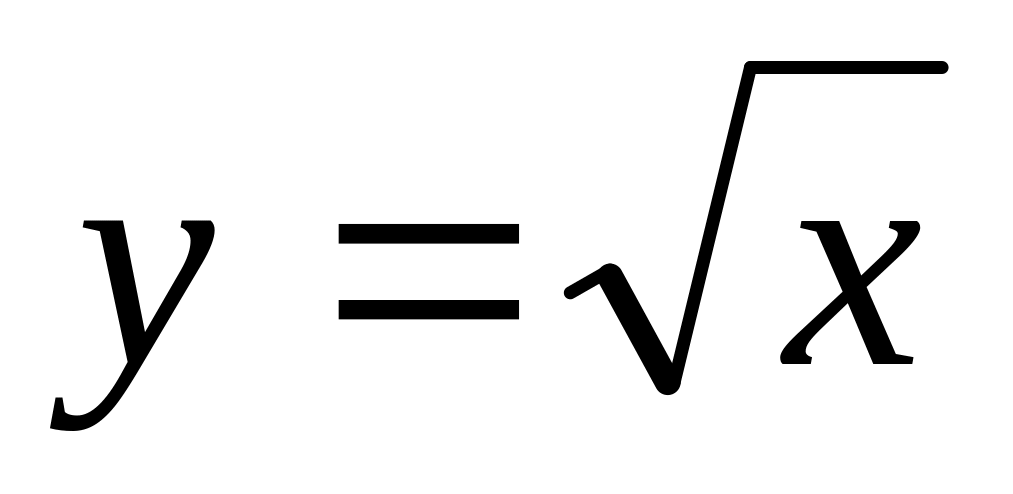от точки до точки .

Решение

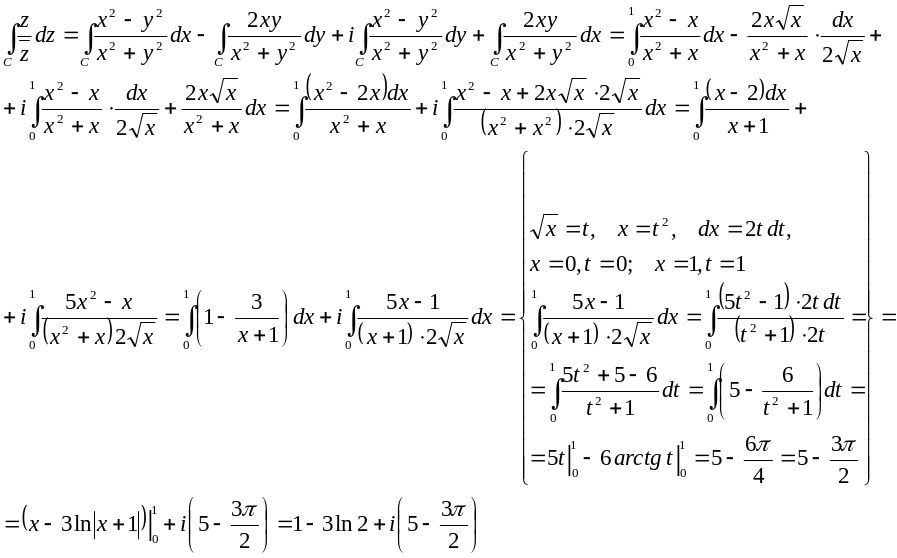
№2772. Вычислить интеграл по следующим путям:

1. По отрезку прямой, соединяющему начало координат с точкой .

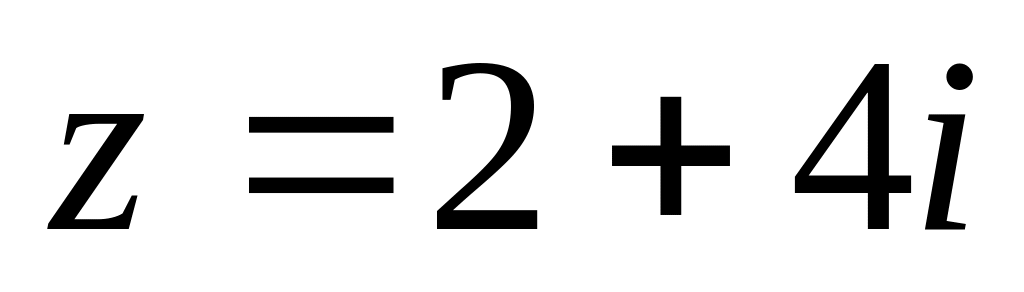Решение

Найдем уравнение прямой:

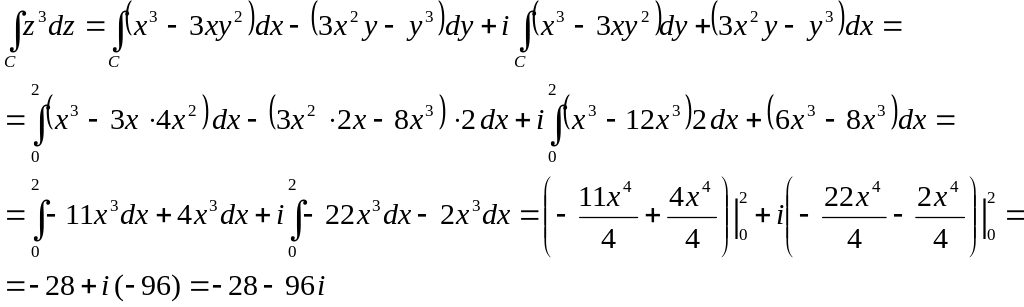
2. По дуге параболы от точки до точки .

Решение