
- •Тема 1. Матрицы и определители
- •Матрицы.
- •1.2.2. Свойства операций сложения (вычитания) матриц:
- •1.2.3. Умножение матрицы на число.
- •1.3. Умножение матриц.
- •1.3.3. Пример.
- •1.4.10.Свойства определителей.
- •1.5. Обратная матрица.
- •1.6.3. Элементарными преобразованиями над матрицей называются преобразования вида:
- •Тема 2. Системы линейных уравнений. (Лекции№3-4)
- •Основные определения.
- •2.3. Совместность систем алгебраических уравнений.
- •Матричный способ решения систем линейных алгебраических уравнений.
- •2.5. Решение систем линейных уравнений методом Гаусса.
- •2.5.3. Последовательность элементарных преобразований расширенной матрицы системы.
- •Решение однородных систем линейных уравнений.
- •Решение систем однородных линейных уравнений:
- •Контрольное домашнее задание №3. Тема: Системы линейных уравнений.
- •Тема 3. Векторная алгебра. (Лекции№5-6)
- •3.1. Общие определения
- •3.2. Линейные операции над векторами.
- •3.3. Действия над векторами в координатной форме
- •3.4. Базис на плоскости и в пространстве.
- •3.4.1. Линейная зависимость и независимость векторов.
- •3.4.4. Выводы:
- •3.4.11. Расстояние между двумя точками в пространстве.
- •3.4.12. Деление отрезка в заданном отношении.
- •3.5. Скалярное произведение векторов.
- •3.5.2. Свойства скалярного произведения:
- •3.6. Векторное произведение двух векторов.
- •3.7. Смешанное произведение трех векторов.
- •3.8. Практическое занятие№4. «Нелинейные операции с векторами»
3.6. Векторное произведение двух векторов.
3.6.1.
Векторным
произведением двух векторов
и
![]() называется третий вектор
называется третий вектор
![]() ,
модуль
которого равен площади параллелограмма,
построенного на векторах
и
,
приведенных к общему началу, и который
перпендикулярен перемножаемым векторам
и направлен в такую сторону, чтобы
кратчайший поворот от
к
вокруг
происходил против часовой стрелки, если
смотреть из конца вектора
.
Обозначение
векторного
произведения
,
модуль
которого равен площади параллелограмма,
построенного на векторах
и
,
приведенных к общему началу, и который
перпендикулярен перемножаемым векторам
и направлен в такую сторону, чтобы
кратчайший поворот от
к
вокруг
происходил против часовой стрелки, если
смотреть из конца вектора
.
Обозначение
векторного
произведения
![]() .
.
3.6.2. Свойства векторного произведения:
 .
. , .
Векторы , и образуют правую тройку, то есть переход от одного к другому происходит против часовой стрелки.
 .
.

 .
.

 ,
где –
число.
,
где –
число.(1

 ,
где
1
и 2
–числа.
,
где
1
и 2
–числа.
3.6.3. Необходимое и достаточное условие коллинеарности двух векторов:
![]() .
.
3.6.4. Векторное произведение двух базисных ортов равно третьему, если они составляют правую тройку:
![]() ,
,
![]() ,
,
![]() , но
, но
![]() .
.
3.6.5. Векторное произведение выражается через координаты своих сомножителей следующим образом. Пусть , , тогда, используя свойства 2. и 4. получим:
![]()
![]()
![]() =
=
= .
(6)
.
(6)
3.6.6. Пример.
Дано:
![]() ,
,
![]() .
Вычислить
,
его модуль (площадь параллелограмма,
построенного на перемножаемых векторах).
.
Вычислить
,
его модуль (площадь параллелограмма,
построенного на перемножаемых векторах).
Решение.
1.
 =
=![]() ==
–7
==
–7
![]() +14
+14![]() –7
–7![]() .
.
2.
![]()
3.6.7.
Пример. Дано
![]() ,
.
Найти площадь треугольника, построенного
на этих векторах.
,
.
Найти площадь треугольника, построенного
на этих векторах.
Решение.
1)
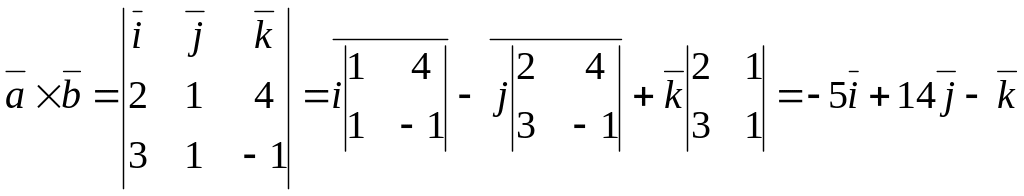 .
.
2)
Находим модуль векторного произведения,
то есть площадь параллелограмма,
построенного на перемножаемых векторах:
![]()
3) Искомая площадь треугольника равна половине площади параллелограмма, то есть S=7,5 ед. кв.
3.7. Смешанное произведение трех векторов.
3.7.1.
Смешанным произведением трех векторов
называется число, равное скалярному
произведению вектора
![]() на вектор
на вектор
![]() .
Обозначение: (
.
Обозначение: (![]()
или
или
![]() c.
c.
Формулу для вычисления смешанного произведения получают умножением склярно вектора на вектор :
(

![]()

(7)
(7)
Свойства смешанного произведения:
*
Операции векторного и скалярного
произведения можно менять местами, то
есть (
=![]()
).
).
*
Смешанное произведение не меняется при
круговой перестановке его сомножителей,
то есть
![]() =
=
.
При нарушении порядка расстановки
векторов произведение меняет знак.
=
=
.
При нарушении порядка расстановки
векторов произведение меняет знак.
Геометрическая интерпретация смешанного произведения трех некомпланарных векторов: его модуль равен объему параллелопипеда, построенного на перемножаемых векторах как на ребрах.
Выводы:
–Условие компланарности трех векторов: если смешанное произведение =0, то эти векторы компланарны.
–Три вектора линейно зависимы, если их смешанное произведение равно нулю, так как три вектора на плоскости линейно зависимы.
3.8. Практическое занятие№4. «Нелинейные операции с векторами»
3.8.1. Примеры решения задач.
1). Вычислить смешанное произведение векторов =(2, 5, 0) ; =(-3, 7, 0) ;
=(0, 0, 2).
Решение.
=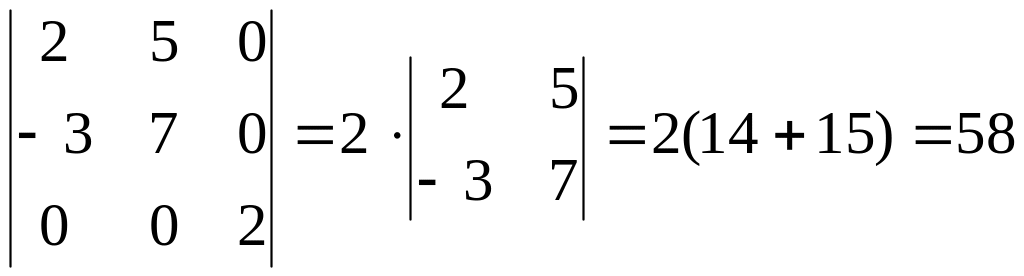 .
.
2) . Проверить компланарны ли вектора W(1,0,3), V(1,2,0) , и R(1,1,).
Решение.
Вычисляем смешанное : WVR
= .
Смешанное произведение трех векторов
не равно нулю. Следовательно, эти вектора
не компланарны.
3) Для векторов
АВ=2i+5j+к
и АС=–3i+7j–к
найти скалярное
(АВАС)
и векторное
произведения N=
АВАС,
угол между
АВ и
АС, вычислить
смешанное произведение трех векторов
(АВАСN)
и
определить
компланарны ли эти вектора.
.
Смешанное произведение трех векторов
не равно нулю. Следовательно, эти вектора
не компланарны.
3) Для векторов
АВ=2i+5j+к
и АС=–3i+7j–к
найти скалярное
(АВАС)
и векторное
произведения N=
АВАС,
угол между
АВ и
АС, вычислить
смешанное произведение трех векторов
(АВАСN)
и
определить
компланарны ли эти вектора.
Решение.
* Находим скалярное произведение двух векторов (АВАС)=2(-2)+57-1=28.
* Вычисляем косинус
угла между этими векторами:
![]()
* Находим векторное произведение векторов N= АВАС=
= ,
затем вычисляем смешанное произведение
трех векторов:
,
затем вычисляем смешанное произведение
трех векторов:
(АВАСN)= 984.
984.
3.8.3. Контрольное домашнее задание № 4. Тема: Нелинейные операции над векторами. Исходные данные по вариантам:
1. АВ=(1,2,2), АС=(3,3,-3). 2. АВ=(-1,2,-2), АС=(-3,3,3).
3. АВ=(2,2,-1), АС=(3,-3,3). 4. АВ=(1,2,2), АС=(3,3,-3).
5. АВ=(1,–2,2), АС=(2,6,-3). 6. АВ=(1,2,2), АС=(6,2,-3).
7. АВ=(1,2,2), АС=(3,2,-6). 8. АВ=(1,2,2), АС=(2,4,-4).
9. АВ=(4,2,4), АС=(3,3,-3). 10. АВ=(–4,–4,2), АС=(3,3,-3).
11. АВ=(–4,4,2), АС=(1,2,-2). 12. АВ=(1,2,2), АС=(6,2,-3).
13. АВ=(1,2,2), АС=(6,3,-2). 14. АВ=(4,6,12), АС=(3,3,-3).
15. АВ=(6,12,–4), АС=(3,3,-3). 16. АВ=(1,2,2), АС=(–6,4,-12).
17. АВ=(1,2,2), АС=(6,12,-4). 18. АВ=(1,2,2), АС=(2,1,-2).
Задание: 1.Найти вектор N= АВАС, вычислить модули векторов, скалярное произведение векторов (АВАС) и косинус угла ВAС. 2. Вычислить смешанное произведение трех векторов (АВАСN), определить компланарны ли эти вектора
Доцент кафедры ММИЭ Шапошников Б.И.
