67

5.3. Дисперсия

В теории измерений важное значение имеет 2-ой центральный момент, называемый дисперсией результатов наблюдений, или дисперсией случайной погрешности D[X].

Для случайной непрерывной величины:

D[X]=D[ ]=M[(X-m_x)²]=M[ ²] = (X-m_x)²p_х(x)dx= ²p_( )d . . . . (5.13).

Для случайной дискретной величины:

D[X]=μ₂= . . . . . . . . . . .(5.14),

где = . . . . . . . .(5.15).

Дисперсией случайной дискретной величины является математическое ожидание разницы квадрата отклонений каждого значения этой величины от ее математического ожидания: D(X)=M[X-M(X)]². Исходя из этого определения, для того, чтобы найти дисперсию, надо вычислить сумму произведений возможных значений квадрата отклонения на их вероятности.

Пример. Найти дисперсию случайной величины Х, которая задана следующим законом распределения:

Х	1	2	5
р	0,3	0,5	0,2

Найдем математическое ожидание величины Х:

М (Х )=1·0,3+2·0,5+5·0,2=2,3.

Определим все возможные значения квадратов отклонений:

[x₁-M(X)]²=(1-2,3)²=1,69,

[x₂-M(X)]²=(2-2,3)²=0,09,

[x₃-M(X)]²=(5-2,3)²=7,29.

Закон распределения величин [x₁-M(X)], [x₂-M(X)]², [x₃-M(X)]² тот же, что и Х.

Отсюда дисперсия:

D(X) = M[X-М(X)]²=1,69·0,3+0,09·0,5+7,29·0,2=0,507+0,045+1,458=2,01.

Не сложно доказать, что дисперсия равна разности между математическим ожиданием квадрата случайной величины и квадратом ее математического ожидания:

D(X)=M[X-M(X)]²=М[Х²-2ХМ(Х)+М²(Х)]=М(Х²)-2М(Х)М(Х)+М²(Х),

поскольку математическое ожидание М(Х) является величиной постоянной, то 2М(Х) и М²(Х) также постоянные величины. Следовательно D(X)=М(Х²) -[М(Х)]².

Найдем дисперсию случайной величины предыдущего примера по этой формуле:

М(Х²)=1·0,3+4·0,5+25·0,2=0,3+2,0+5,0=7,3,

М(Х)=1·0,3+2·0,5+5·0,2=0,3+1,0+1,0=5,29

D(X)=М(Х²) -[М(Х)]²=7,3-5,29=2,01.

Дисперсия случайной погрешности является характеристикой рассеяния результатов наблюдений относительно математического ожидания.

Дисперсия имеет размерность квадрата измеряемой физической величины, поэтому значительно чаще в метрологической практике пользуются средним квадратическим отклонением (СКО) результатов наблюдений, являющимся квадратным корнем из дисперсии: = СКО имеет размерность измеряемой физической величины.

Плотность вероятности результатов наблюдений при различных значениях СКО погрешности имеет следующий вид:

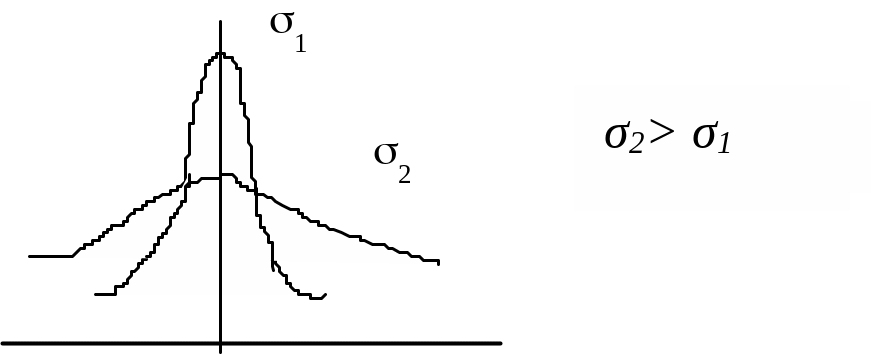
Рис. 5.4

Чем больше , тем более пологой и «расплывчатой» становится функция распределения.

Дисперсия обладает четырьмя свойствами.

Свойство 1. Дисперсия постоянной величины равно нулю: D(C)=0.

Доказательство. По определению дисперсия случайной величины равна разницы квадрата отклонений каждого значения этой величины и ее математического ожидания: D(X)=M[X-M(X)]². Тогда D(С)=M[С-M(С)]². В соответствии с первым свойством математического ожидания (математическое ожидание постоянной величины равно самой величине) имеем: D(С)= M(С-С) ²=М(0)²=0. Это говорит также о том, что постоянная величина сохраняет одно и то же значение и рассеяния не имеет.

Свойство 2. Постоянный множитель можно выносить за знак дисперсии, возведя его в квадрат:

D (CX)=C²D(X). . . . . . . (5.16).

Доказательство. По определению дисперсия случайной величины D(CX)=М[CX-M(CX)²]. В соответствии со вторым свойством математического ожидания (постоянный множитель можно выносить за знак математического ожидания)

D(CX)=M[CX-CM(X)]²=M[C²(X-M(X)²]=C²M[X-M(X)]²=C²D(X).

Свойство 3. Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин: D(X+Y)=D(X)+D(Y). . . . . (5.17).

Доказательство. По формуле для дисперсии имеем:

D(X+Y) = M[(X+Y)²]-[M(X+Y)]².

Раскрыв скобки, и используя свойство математического ожидания суммы нескольких величин и произведения двух независимых случайных величин, получим:

D(X+Y)=M[(X²+2XY+Y²)]-[M(X)+M(Y)]²=M(X²)+2M(X)·M(Y)+M(Y²)-M²(X)-2M(X)·M(Y)-M²(Y)=M(X²)-[M(X)]²+M(Y²)-[M(Y)]²=D(X)+D(Y).

Следствиями этого свойства является то, что дисперсия суммы нескольких взаимно независимых случайных величин равна сумме дисперсий этих величин, а также то, что дисперсия суммы постоянной величины и случайной величины равна дисперсии случайной величины, т.е. ·D(C+X)=D(C)+D(X)=D(X). . . . . (5.18).

Свойство 4. Дисперсия разности двух независимых случайных величин равна сумме дисперсий этих величин: D(X-Y) = D(X)+D(Y).

Доказательство. В силу третьего свойства D(X-Y)= D(X)+ D(-Y). По второму свойству дисперсии D(-Y)=(-1)² D(Y)= D(Y). Следовательно, D(X-Y)= D(X)+ D(Y). .(5.19).

На основании этого свойства среднее квадратическое отклонение суммы конечного числа взаимно независимых случайных величин равно квадратному корню из суммы квадратов средних квадратических отклонений этих величин:

σ(Х₁+ Х₂+…+Х_n)= . . . .(5.20).

Известно, что по закону распределения можно найти числовые характеристики случайной величины. Это в свою очередь означает, что если несколько случайных величин имеют одинаковые законы распределения, то их числовые характеристики одинаковы.

Рассмотрим n независимых случайных величин Х₁, Х₂, …, Х_n, которые имеют одинаковые распределения, а следовательно, и одинаковые характеристики (математическое ожидание, дисперсию и др.). С точки зрения теории измерений наибольший интерес представляет изучение числовых характеристик среднего арифметического этих величин.

Обозначив среднее арифметическое рассматриваемых случайных величин как = , установим связь между числовыми характеристиками этого среднего арифметического и соответствующими характеристиками математического ожидания, дисперсии и среднего квадратического отклонения среднего арифметического значения случайной величины.

1.Математическое ожидание среднего арифметического одинаково распределенных взаимно не связанных случайных величин равно математическому ожиданию а каждой из величин: М ( ) = а.

2.Дисперсия среднего арифметического n одинаково распределенных независимых случайных величин в n раз меньше дисперсии D каждой из величин: D ( )=D/ n.

3.Среднее квадратическое отклонение среднего арифметического n одинаково распределенных независимых случайных величин в раз меньше среднего квадратического отклонения σ каждой из величин: σ ( ) = σ/ .

Пример. Среднее квадратическое отклонение каждой из 16 одинаково распределенных взаимно независимых случайных величин равно 10. Найти среднее квадратическое отклонение среднего арифметического этих величин.

=