4.Разложение в ряд Фурье четных и нечетных функций
Если разлагаемая на отрезке в ряд Фурье функция является четной или нечетной, то это отражается на формулах коэффициентов Фурье (вычисление их упрощается) и на виде самого ряда (он становится неполным).
Приведем здесь несколько очевидных свойств четных и нечетных функций.
1. Произведение четной функции на четную функцию есть функция четная.
2. Произведение нечетной функции на нечетную функцию есть функция четная.
3. Произведение четной функции на нечетную функцию есть функция нечетная.
4. Если
-
четная функция, то
.
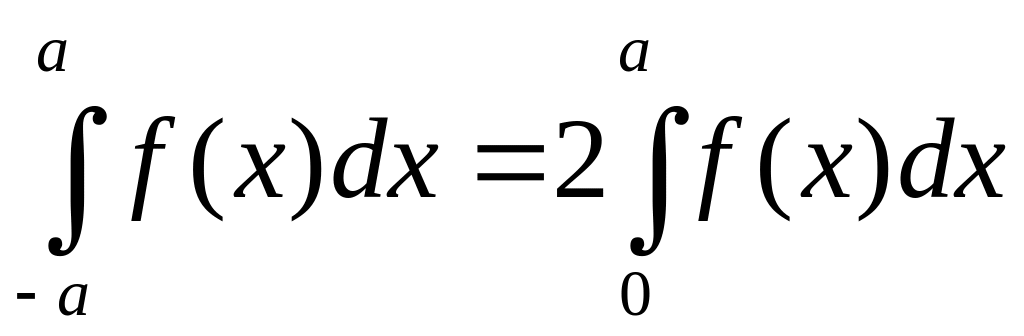5. Если
-
нечетная функция, то
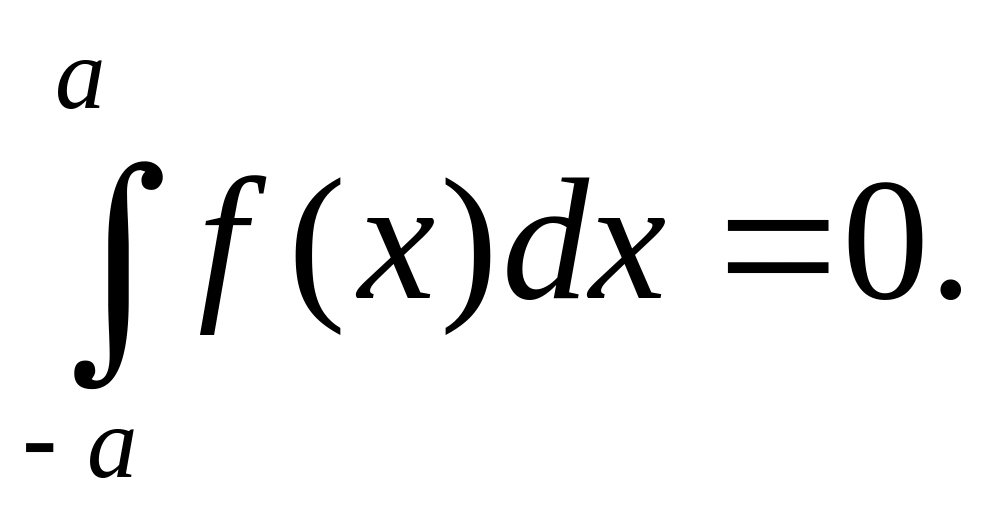
Используя указанные свойства, вычислим коэффициенты Фурье и построим ряды Фурье для четной и нечетной функций.
Если функция четная, то коэффициенты Фурье приобретают вид:
Ряд Фурье для
четной функции:
.
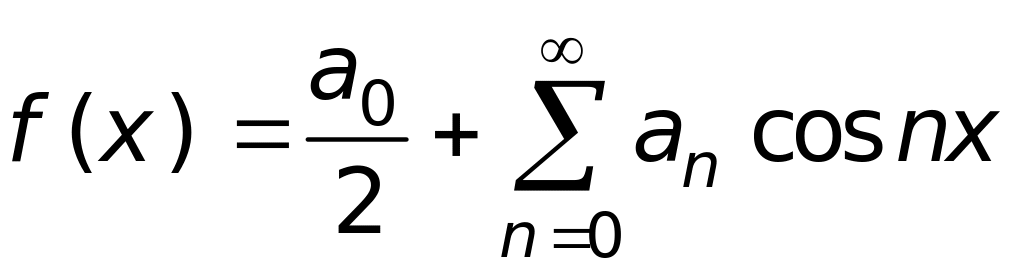Если функция нечетная, то коэффициенты Фурье приобретают вид:
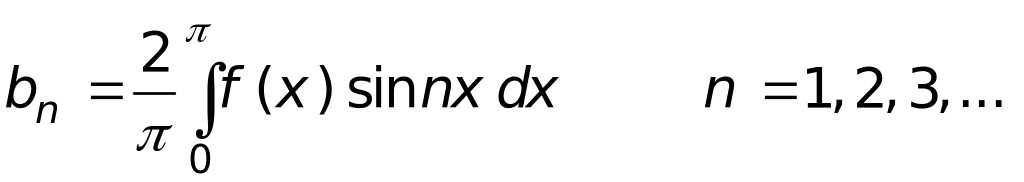
Ряд Фурье для
нечетной функции:
.
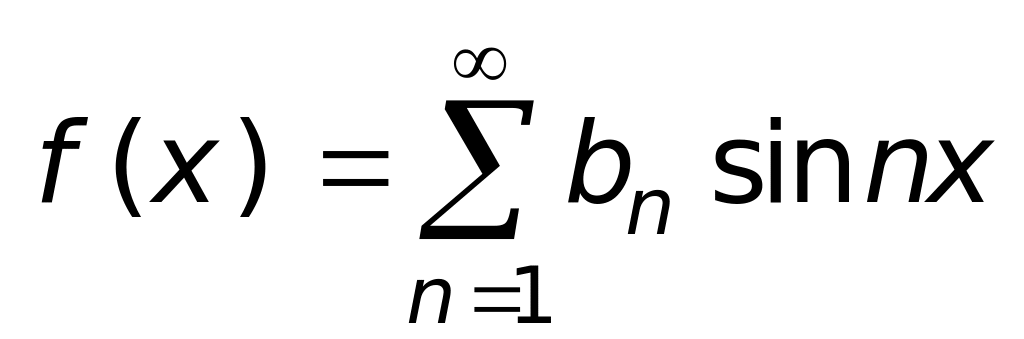Такие неполные тригонометрические ряды часто называют рядами по косинусам или рядами по синусам, а разложения функций разложение по синусам или разложение по косинусам.
Пример.
Разложить в ряд
Фурье функцию периода 2,
заданную на интервале
формулой
Функция четная, поэтому коэффициенты Фурье определяются так:
Таким образом,
Ряд Фурье, соответствующий функции , имеет вид
Данная функция удовлетворяет условиям теоремы Дирихле, следовательно, ряд сходится на всей числовой оси и имеет своей суммой функцию .
5.Разложение в ряд Фурье функций произвольного периода
Разлагать в ряд Фурье можно и периодические функции с периодом отличным от .
Пусть функция
,
определенная на отрезке
,
имеет период
и удовлетворяет на этом отрезке условиям
Дирихле.
Сделав подстановку
,
данную функцию
преобразуем в функцию
,
которая определена на отрезке
и имеет период
.
Разложение функции
в ряд Фурье на отрезке
имеет вид
,
где
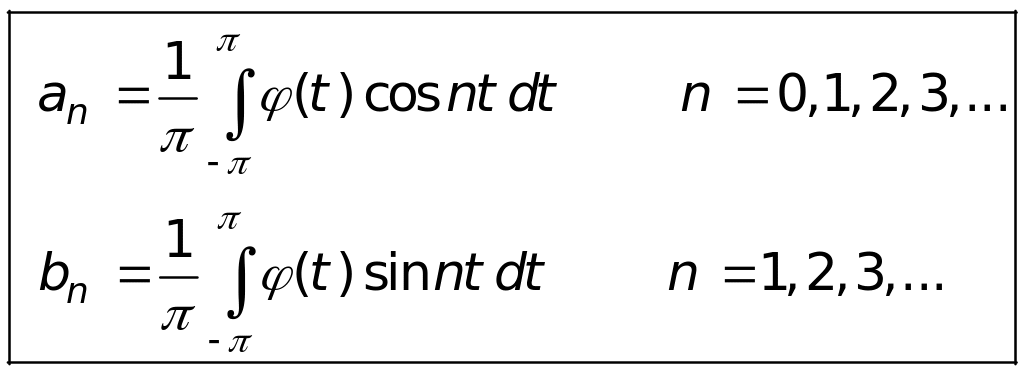
Возвращаясь к
исходной переменной, и учитывая
,
получим
Правила разложения четных и нечетных функций и здесь остаются в силе.
Пример.
Разложить в ряд
Фурье функцию, заданную в промежутке
уравнением
.
Решение. Разложение в ряд Фурье необходимо выполнить только на интервале изменения аргумента , поэтому функцию можно представить периодической с периодом равным 2 (см. рис. 6).
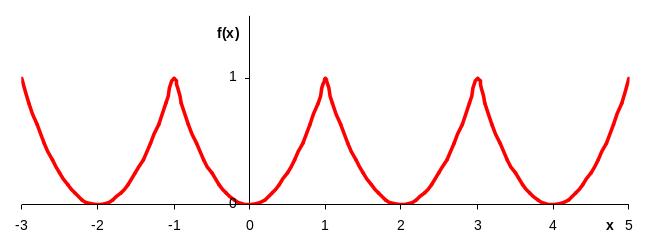
Рис. 6. График функции в заданном интервале изменения аргумента с периодическим продолжением на оси
Заданная функция
является четной, определенной в интервале
,
поэтому коэффициенты ряда Фурье равны
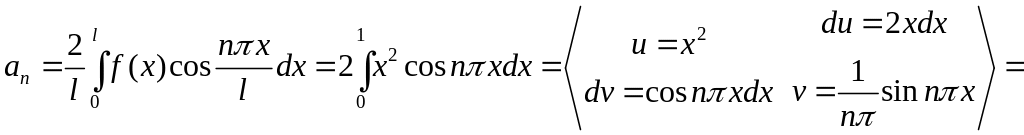
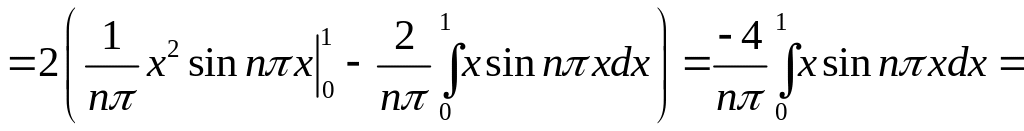
В итоге получаем искомый ряд Фурье
.
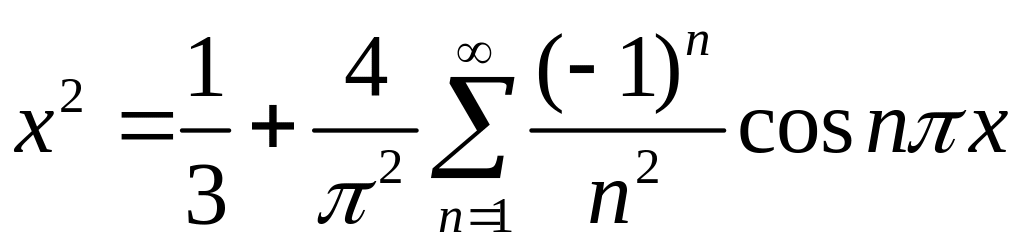Ниже (рисунки 7 и 8) приведена графическая иллюстрация к решению примера.
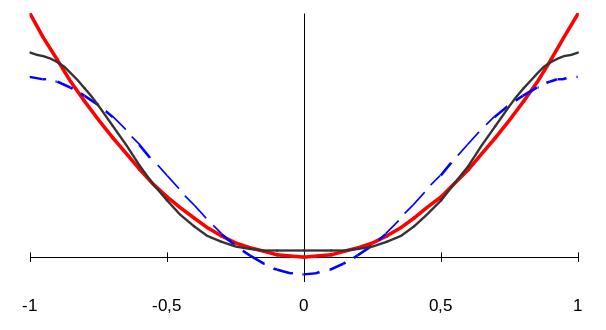
Рис.7. Графики исходной функции (толстая кривая), суммы нулевого и первого члена (пунктир), суммы нулевого, первого и второго членов ряда (тонкая кривая)
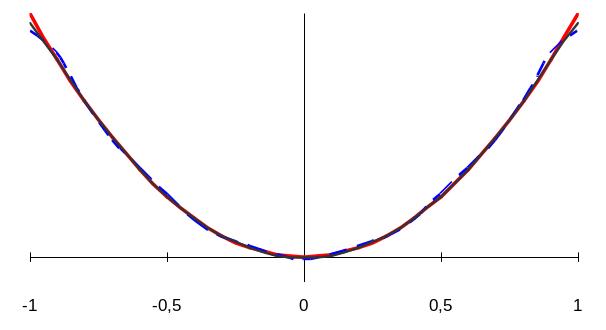
Рис.8. Графики исходной функции (толстая кривая), суммы нулевого и трех первых членов ряда (пунктир), суммы нулевого и пяти первых членов ряда (тонкая кривая)
6. Представление непериодической функции рядом Фурье
Пусть - непериодическая функция, заданная на всей числовой оси. Так как сумма тригонометрического ряда является периодической функцией, то, очевидно, что данная непериодическая функция не может быть разложена в ряд Фурье.
Рассмотрим теперь
эту функцию на интервале
и попытаемся построить ряд Фурье, который
имел бы ее своей суммой в этом интервале.
Следует отдельно отметить, что построенный
ряд Фурье справедлив, как разложение
заданной функции только (и только) на
интервале
,
а не на всей числовой оси.
Для построения
ряда Фурье рассмотрим вспомогательную
функцию
с периодом
,
значения которой совпадают со значениями
функции
.
Если для функции
выполняются условия теоремы Дирихле,
то ее можно представить соответствующим
рядом Фурье. Этот ряд на интервале
во всех точках непрерывности функции
имеет своей суммой
=
.
Иначе говоря,
вместо заданной функции в ряд Фурье
разлагается вспомогательная периодическая
функция с симметричным (относительно
)
интервалом. Так как суммы полученного
ряда аппроксимируют вспомогательную
функцию на интервале
,
то этот ряд можно использовать и для
исходной функции, но только на указанном
на интервале
,
Иногда приходится
иметь дело с функциями, заданными только
в интервале
.
В этом случае мы можем сначала продолжить
(доопределить) по какому-либо закону
функцию на интервал
, а затем продолжить ее на всю числовую
прямую периодически с периодом
.
Продолжить функцию из интервала
на интервал
можно произвольным образом.
Чаще всего продолжают четным или нечетным образом. Если функция продолжается четным образом, то ряд Фурье содержит только косинусы и свободный член. Если же функция продолжается нечетным образом, то ряд Фурье содержит только синусы.
Пример.
Разложить в ряд косинусов функцию
.
Решение. Продолжим
функцию
на отрезок
четным образом.
Разлагаем в ряд
функцию
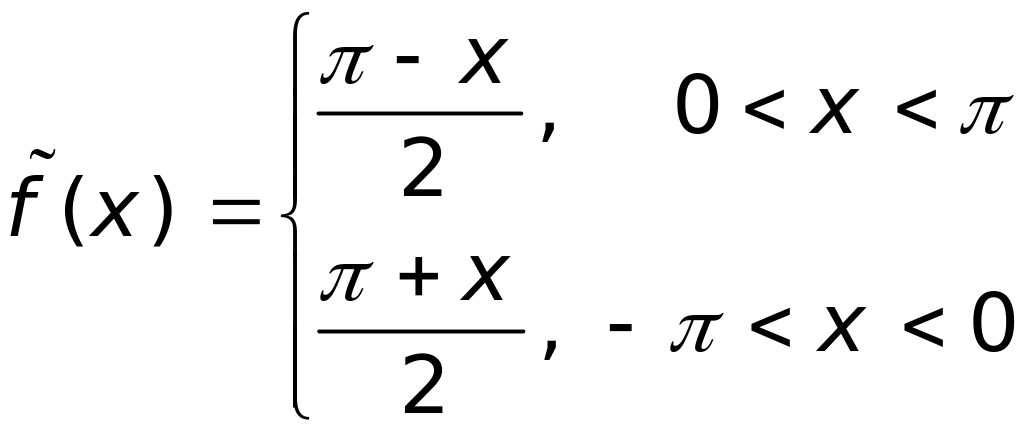с периодом
.
Функция удовлетворяет условиям теоремы Дирихле, поэтому
.
Таким образом
,
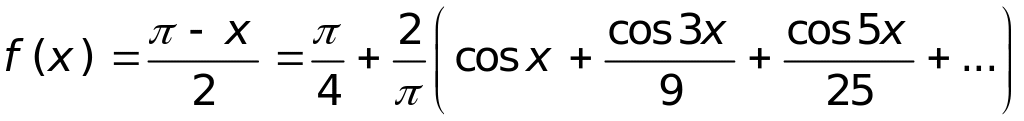где
.