2.Тригонометрический ряд Фурье
Покажем, что практически любую периодическую функцию можно представить в виде ряда, членами которого являются простые гармоники, с помощью, так называемого, тригонометрического ряда.
Тригонометрическим рядом называется функциональный ряд вида
где действительные
числа
-
называются коэффициентами
ряда.
Свободный член
ряда записан в виде
для единообразия получающихся в
дальнейшем формул.
Приведем формулы, которые понадобятся нам в дальнейшем.
Считая
и
целыми положительными, находим:
Предположим, что
функция
оказалась такой, что для неё нашлось
разложение в сходящийся ряд Фурье, то
есть
.
(*)
(Следует обратить
внимание, что суммирование идёт по
индексу
).
Если ряд сходится,
то его сумму обозначим
.
Почленное
интегрирование (законное в силу
предположения о сходимости ряда) в
пределах от
до
даёт
Умножая (*) на
и почленно интегрируя в пределах от
до
,
получим
Умножая (*) на
и почленно интегрируя в пределах от
до
,
получим
При вычислении
трех последних интегралов учтено, что
только некоторые из слагаемых равны
только при
.
Именно поэтому в правых частях у
коэффициентов ряда выполнена замена
индекса
на индекс
.
Итак, получаем
выражения для коэффициентов разложения:
(**)
Числа , определяемые по вышеприведенным формулам, называются коэффициентами Фурье, а тригонометрический ряд с такими коэффициентами – рядом Фурье.
3.Разложение в ряд Фурье 2-периодических функций
Пусть - произвольная периодическая функция с периодом 2
Выясним условия, при которых ряд Фурье функции сходится и имеет своей суммой как раз функцию .
Будем рассматривать
функции
,
имеющие период
.
Такие функции называются
-
периодическими.
Сформулируем теорему, представляющую достаточное условие разложимости функции в ряд Фурье.
Теорема Дирихле
(примем без доказательства).
Пусть
-периодическая
функция
на отрезке
удовлетворяет двум условиям:
1. кусочно-непрерывна, т.е. непрерывна или имеет конечное число точек разрыва I рода;
2. кусочно-монотонна, т.е. монотонна на всем отрезке, либо этот отрезок можно разбить на конечное число интервалов так, что на каждом из них функция монотонна.
Тогда соответствующий функции ряд Фурье сходится на этом отрезке и при этом:
1. В точках
непрерывности функции сумма ряда
совпадает
с самой функцией:
.
2. В каждой точке
разрыва функции сумма ряда равна
т.е. равна среднему арифметическому пределов функции справа и слева.
3. В точках
и
(на концах отрезка) сумма ряда равна
Таким образом, если интегрируемая на отрезке функция удовлетворяет условиям теоремы Дирихле, то на отрезке имеет место равенство (разложение в ряд Фурье):
и говорят: функции соответствует (поставлен в соответствие) её ряд Фурье.
Условиям Дирихле удовлетворяет большинство функций, которые встречаются в математике и ее приложениях.
Пример 1.
Разложить в ряд
Фурье функцию
с периодом 2,
заданную на интервале
формулой
.
Решение. Найдем коэффициенты ряда Фурье:
.
При вычислении последних интегралов использовался метод интегрирования по частям.
При вычислении
интеграла учтено, что при любом целом
очевидны равенства
и
.
Получаем следующие коэффициенты ряда
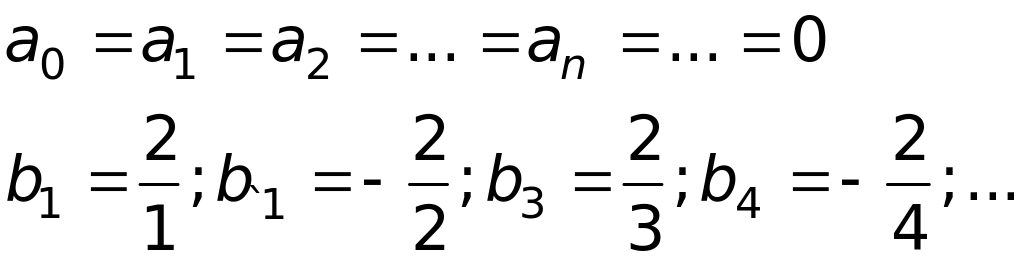
Следовательно, ряд Фурье для заданной функции имеет вид
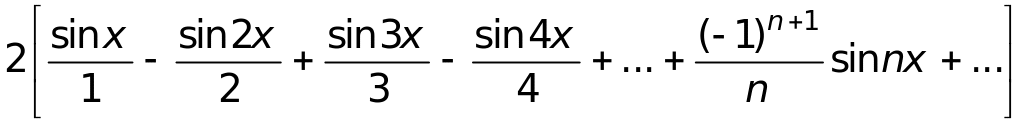
Окончательно
получаем:
Так как функция удовлетворяет условиям Дирихле, то в любой точке непрерывности сумма ряда равна значению функции.
Из этого разложения можно получить интересное следствие.
Полагая
,
получим
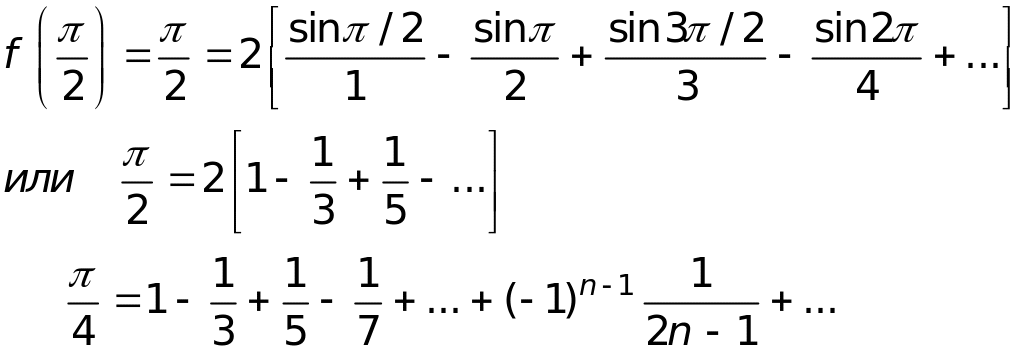
Пример 2.
Разложить в ряд
Фурье
-периодическую
функцию, заданную на отрезке
формулой
Решение. На рис.1 изображен график данной функции
Находим коэффициенты ряда:
А
налогично
находим
.
Рис.1. График заданной для разложения функции
Итак, исходной функции соответствует ряд Фурье
Пример 3.
Разложить в ряд
Фурье
-периодическую
функцию
.
Решение. График
функции вместе с периодическим
продолжением на оси
показан на рис.2
Найдем коэффициенты искомого ряда Фурье:
Рис. 2. График - периодической функции
Последний интеграл вычисляем с использованием метода интегрирования по частям:
Окончательно
получаем
.
Для значений
=
1,2,… получаем
Для значений
=
1,2,… получаем
Искомый ряд Фурье записываем в виде
или (с учетом вычисленных коэффициентов ряда)
.
На рис. 3 показан график исходной функции, а также графики: сумм нулевого и первого членов ряда, сумм нулевого, первого и второго членов ряда.
Рис. 3. Графики исходной функции (толстая линия), суммы двух членов разложения (пунктир), суммы 3 членов разложения (сплошная кривая)
На рис. 4 показан график исходной функции, а также графики: сумм нулевого члена ряда и членов ряда с 1-го по 5-ый, сумм нулевого члена ряда и членов ряда с 1-го по 10-ый.
Рис. 4. Графики исходной функции (толстая линия), суммы 6 членов разложения (пунктир), суммы 11 членов разложения (сплошная кривая)
На рис.5 показан график исходной функции, а также графики: сумм нулевого члена ряда и членов ряда с 1-го по 20-ый, сумм нулевого члена ряда и членов ряда с 1-го по 50-ый.
Рис. 5. Графики исходной функции (толстая линия), суммы 21 членов разложения (пунктир), суммы 51 членов разложения (сплошная кривая)