
- •2. Дифференцируемость и аналитичность
- •3. Элементарные функции комплексной переменной
- •Операционное исчисление Содержание:
- •1. Функция оригинал и изображение по Лапласу
- •2. Теоремы преобразования Лапласа
- •3. Методы определения оригинала по известному изображению
- •4. Решение дифференциальных уравнений и систем операционным методом.
- •5. Примеры решения задач
- •5.1 Пример выполнения задания 1
- •5.2. Рекомендация к выполнению задания 2
- •5.4 Пример выполнения задания 4
- •6. Вопросы и задачи для самостоятельной работы
1. Функции комплексной переменной. Непрерывность. Области и границы
Если
х
и
у
-
действительные переменные,
![]() -
мнимая единица, то переменная
-
мнимая единица, то переменная
![]() называется
комплексной переменной. Действительную
и мнимую
части комплексной переменной Z
обозначают
называется
комплексной переменной. Действительную
и мнимую
части комплексной переменной Z
обозначают
![]() .
.
Если
каждому значению Z
из
множества Z
поставить
в соответствие одно или
несколько значений другой комплексной
переменной![]() то
комплексная
переменная
W
называется
функцией Z
в
области Z,
и
пишут
то
комплексная
переменная
W
называется
функцией Z
в
области Z,
и
пишут
![]()
Функция![]() называется
однозначной, если каждому значению
называется
однозначной, если каждому значению
![]() ,
ставится
в соответствие только одно значение W,
и
многозначной, если несколько
значений W.
,
ставится
в соответствие только одно значение W,
и
многозначной, если несколько
значений W.
Если![]() - действительная
часть функции W,
- действительная
часть функции W,
![]() - мнимая
часть функции W,
то
функция
- мнимая
часть функции W,
то
функция
![]() записывается
в
виде суммы действительной и мнимой
части.
записывается
в
виде суммы действительной и мнимой
части.
![]() (1.1)
(1.1)
Однозначная
функция
![]() при
при
![]() имеет
определенный предел с (z0
и с – комплексные числа), если для всякого
имеет
определенный предел с (z0
и с – комплексные числа), если для всякого
![]() найдется
такое число
найдется
такое число
![]() ,
что из неравенства
,
что из неравенства
![]() следует
неравенство
следует
неравенство
![]() .
При
этом пишут
.
При
этом пишут
![]()
Функция
![]() называется
непрерывной в точке
называется
непрерывной в точке
![]() ,
если
она определена в некоторой
окрестности
,
если
она определена в некоторой
окрестности
![]() и в самой этой точке и
и в самой этой точке и![]()
Функция, непрерывная в каждой точке некоторой области D, называется непрерывной в этой области.
Для
непрерывности
![]() в
точке
в
точке
![]() необходимо
и достаточно, чтобы функции
необходимо
и достаточно, чтобы функции
![]() были
непрерывными в точке
были
непрерывными в точке![]()
Пример 1. Исследовать на непрерывность функцию
![]()
РЕШЕНИЕ. Запишем функцию в виде (1).

Отсюда
следует, что функции
![]() и
и
![]() непрерывны на плоскости
непрерывны на плоскости
![]() значит
данная функция W
также
непрерывна на всей комплексной плоскости
Z.
значит
данная функция W
также
непрерывна на всей комплексной плоскости
Z.
Область D - это множество точек, обладающих свойством открытости (вместе с точкой области D принадлежит и достаточно малый круг с центром в этой точке) и свойством связности (две любые точки D можно соединить ломаной, полностью лежащей в D).
Замкнутой областью D называют область D с присоединенной к ней границей Г.
Область D называют ограниченной, если она принадлежит некоторому кругу
![]()
Порядком связности ограниченной области D называется число связных частей, на которые разбивается её граница. Граница может состоять из замкнутых линий, разрезов и точек.
Границы области могут задаваться уравнениями кривых, которые рассмотрим на примере. Пример 2. Определить виды кривых:
a)
![]()
РЕШЕНИЕ
![]() -
уравнение окружности с центром в точке
-
уравнение окружности с центром в точке
![]() и радиусом R.
и радиусом R.
![]()
РЕШЕНИЕ Это уравнение равносильно уравнению.
![]()
![]() и
образующего с положительным направлением
оси X
угол
и
образующего с положительным направлением
оси X
угол
![]()
![]()
РЕШЕНИЕ
В данном случае действительная и мнимая части комплексного переменного заданы параметрически. Исключим параметр t из уравнений
![]() ,
,
![]()
2. Дифференцируемость и аналитичность
Пусть
функция
![]() определена
в некоторой окрестности точки Z.
Функция
дифференцируема в точке
Z,
если
существует предел.
определена
в некоторой окрестности точки Z.
Функция
дифференцируема в точке
Z,
если
существует предел.

Этот
предел называется производной функции
![]() в точке Z. Функция дифференцируемая в
каждой точке области D и имеющая в этой
области непрерывную производную
в точке Z. Функция дифференцируемая в
каждой точке области D и имеющая в этой
области непрерывную производную
![]() называется
аналитической в области D.
называется
аналитической в области D.
Функция
![]() аналитическая в точке,
аналитическая в точке,
![]() если
является аналитической в некоторой
окрестности точки Z0.
если
является аналитической в некоторой
окрестности точки Z0.
Для
того чтобы функция
![]() была
аналитической в области D,
необходимо и достаточно одновременное
существование в этой области непрерывных
частных производных функций
была
аналитической в области D,
необходимо и достаточно одновременное
существование в этой области непрерывных
частных производных функций
![]() удовлетворяющим
условиям Коши-Римана:
удовлетворяющим
условиям Коши-Римана:
 (1.2)
(1.2)
При
выполнении условий (2) производная
![]() может быть вычислена по одной из формул
может быть вычислена по одной из формул
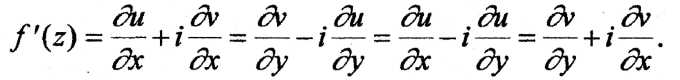 (1.3)
(1.3)
Для
аналитических функций правила
дифференцирования и таблица производных
элементарных функций комплексной
переменной такие же, как для функций
действительной переменной, что
иллюстрирует следующий пример. Пример
3, Проверить выполнение условий Коши-Римана
для функции
![]() является
дифференцируемой и аналитической на
всей комплексной плоскости Z:
является
дифференцируемой и аналитической на
всей комплексной плоскости Z:
![]()
Таким
образом,
![]()
3. Элементарные функции комплексной переменной
1.
Функции комплексной переменной
![]() определяются
как суммы следующих рядов, сходящихся
во всей плоскости комплексного
переменного:
определяются
как суммы следующих рядов, сходящихся
во всей плоскости комплексного
переменного:
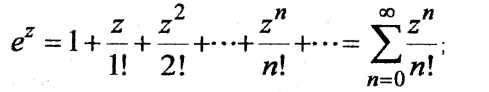 (1.4)
(1.4)
 (1.5)
(1.5)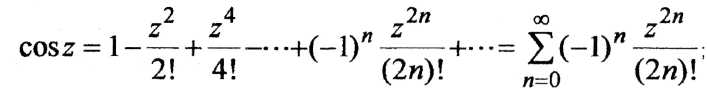 (1.6)
(1.6) (1.7)
(1.7)
 (1.8)
(1.8)
Из определения функций (10.4)-(10.8) следуют формулы, связывающие их:
![]() (1.9)
(1.9)
![]() (1.10)
(1.10)
![]() (1.11)
(1.11)
![]() (1.12)
(1.12)
![]() (1.13)
(1.13)
![]() (1.14)
(1.14)
![]() (1.15)
(1.15)
![]() (1.16)
(1.16)
Элементарные функции (1.4) – (1.8) являются однозначными и непрерывными на всей комплексной области Z.
2.
Показательная функция
![]() совпадает с обычной функцией
совпадает с обычной функцией
![]() для нее справедлива теорема сложения
для нее справедлива теорема сложения
![]()
Функция
![]() периодическая
с чисто мнимым основным периодом
периодическая
с чисто мнимым основным периодом
![]()
![]()
Тригонометрические
функции
![]() для
действительных
для
действительных
![]() совпадает
с обычным синусом и косинусом,
периодичны с действительным периодом
совпадает
с обычным синусом и косинусом,
периодичны с действительным периодом![]() -
нечетная,
-
нечетная,
![]() - четная функция; подчиняются обычным
тригонометрическим соотношениям:
- четная функция; подчиняются обычным
тригонометрическим соотношениям:
![]() и
т.п.
и
т.п.
Функция
![]() называется
гиперболическим синусом; функция
называется
гиперболическим синусом; функция
![]() называется
гиперболическим конусом. Гиперболические
функции
называется
гиперболическим конусом. Гиперболические
функции
![]() выражаются
через тригонометрические функции
формулами (1.15,1.16).
выражаются
через тригонометрические функции
формулами (1.15,1.16).
С помощью функций (1.4) - (1.8) вводятся другие элементарные функции. 3 Логарифмическая функция определяется как функция, обратная показательной:
если:
![]()
Для нее справедливо свойство логарифмов:
![]()
![]() ,
получаем
,
получаем
![]() (1.17)
(1.17)
В
формуле (1.17) символ
![]() может
обозначать любое значение аргумента,
поэтому
каждое комплексное число имеет
бесчисленное множество логарифмов.
может
обозначать любое значение аргумента,
поэтому
каждое комплексное число имеет
бесчисленное множество логарифмов.
Выражение
![]() называется
главным значением
логарифмической
функции и обозначается, как
называется
главным значением
логарифмической
функции и обозначается, как
![]() Многозначная
логарифмическая функция обозначается
Многозначная
логарифмическая функция обозначается
![]()
![]() (1.18)
(1.18)
4. Общая показательная функция:
![]() (1.19)
(1.19)
Эта
функция представляет собой совокупность
отдельных, не связанных между собой
однозначных функции, отличающихся
множителями
![]() где
k-
целое
число. Главное значение этой многозначной
функции равно
где
k-
целое
число. Главное значение этой многозначной
функции равно
![]()
где
![]() -
произвольное комплексное число.
-
произвольное комплексное число.
Полагая,
![]() ,
получаем
,
получаем
![]()
![]() (1.20)
(1.20)
где
![]() -
произвольное комплексное число.
-
произвольное комплексное число.
Полагая
![]() ,
получаем
,
получаем
![]()
![]() (1.21)
(1.21)
где
k
– целое число. При
![]() функция
функция
![]() всегда
имеет бесконечно много значений.
всегда
имеет бесконечно много значений.
Если
![]() ,
то
получаем многозначную функцию - корень
n-й
степени
,
то
получаем многозначную функцию - корень
n-й
степени
![]()
При
![]() имеем
частный случай однозначной степенной
функции
имеем
частный случай однозначной степенной
функции
![]()
К основным элементарным функциям комплексной переменной относится также дробно-рациональная функция и её частные случаи.
Дробно-рациональная функция:
 (1.22)
(1.22)
Частные случаи этой функции:
а)линейная
функция
![]() - комплексные числа
- комплексные числа
б)степенная
функция
![]()
в)дробно-линейная
функция

