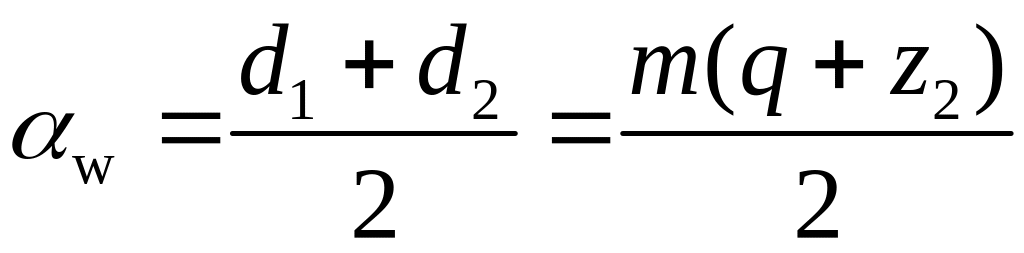7.3 Скольжение в зацеплении червячной передачи. Кпд пе­редачи

7.3.1 Витки червяка скользят по зубьям колеса, как в винто­вой паре. На рисунке 7.7 иллюстрировано зацепление зуба колеса с витком червяка. Будем считать, что их контакт происходит на делительных диа­метрах червяка и колеса . На этом основании окружные скорости в точке контакта для червяка и колеса выразятся соответственно

; .

Таблица 7.1 − Основные геометрические параметры передачи с архимедовым червяком

Наименование параметра	Обозначение, формула
Ч Е Р В Я К
Угол профиля витка в осевом се­чении
Расчетный шаг
Расчетный модуль
Делительный диаметр
Число заходов
Ход витка
Угол подъема линии витка
Диаметр вершин витков
Диаметр впадин витков
К О Л Е С О Ч Е Р В Я Ч Н О Е
Делительный диаметр
Диаметр вершин зубьев
Диаметр впадин зубьев
Наибольший диаметр колеса
Ширина венца колеса	при 1 и 2 при 4
Условный угол обхвата червяка колесом
Межосевое расстояние передачи
Передаточное отношение пере­дачи

Скорость скольжения направлена по касательной к линии витка червяка. Как скорость относительная, она равна геометрической разности абсолютных скоростей червяка и колеса . Из рисунка 7.7 следует, что

.

Так как практически всегда то в червячной передаче

.

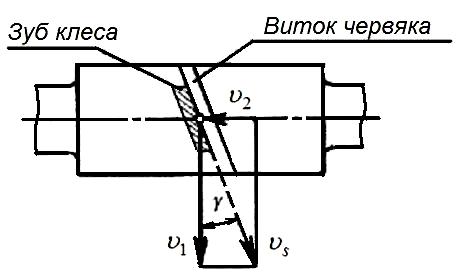
Рисунок 7.7 − Иллюстрация к определению скорости скольжения в зацеплении червячной пары

Скорость скольжения в червячном зацеплении больше окружной скорости как червяка, так и колеса. Это служит причиной понижен­ного КПД передачи и повышенного износа зубьев.

В зацеплении зубчатых колес скольжение также имеется (см. под­раздел 4.5). Но здесь его скорость всегда значительно меньше окружных скоростей зубьев в точке зацепления. Поэтому КПД зубчатой передачи всегда выше, чем КПД червячной передачи и к тому же он более стаби­лен (см. таблицу 2.1).

7.3.2 КПД червячной передачи, как и передачи зубчатой, выража­ется формулой (2.7). В неё, помимо потерь в подшипниках и потерь гид­равлических, входят потери в зацеплении . В отношении червячной передачи потери в зацеплении рассматривают для двух случаев, когда ведущий червяк и когда ведущее колесо.

При ведущем червяке КПД зацепления

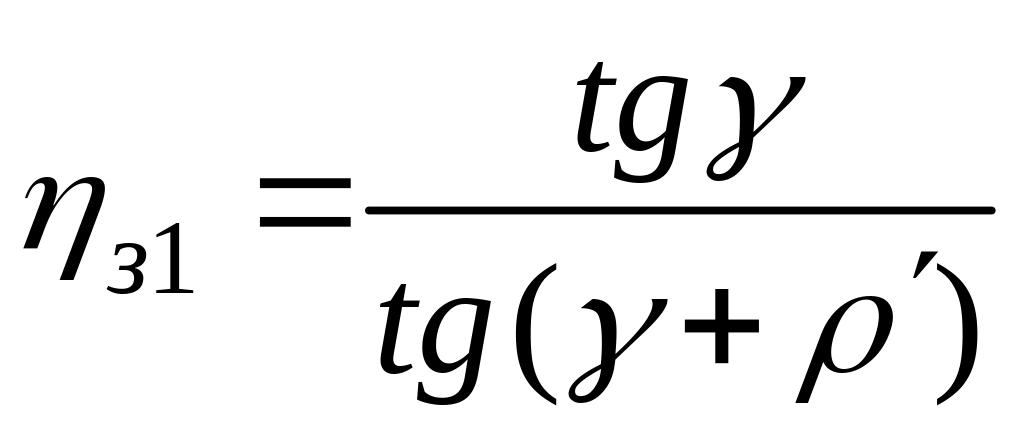, (7.1)

где − угол подъема линии витка червяка (см. пункт 7.2.8);

− приведенный угол трения.

Если ведущим звеном передачи является колесо, то КПД зацепле­ния

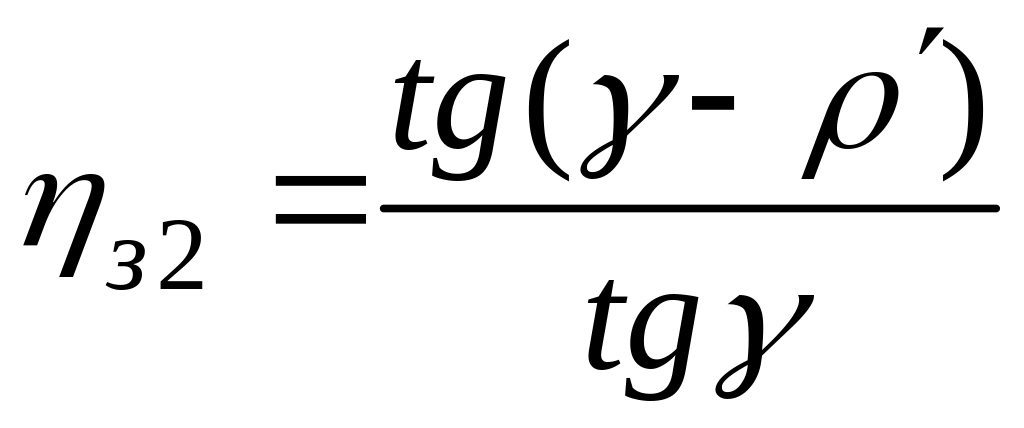. (7.2)

Примечания:

1 Напомним, что в теоретической механике углом трения назы­вают угол, тангенс которого равен коэффициенту трения.

2 Формулы (7.1) и (7.2) заимствованы из теории винтовой пары и приводятся без вывода (7, с. 179).

Если проанализировать, как меняется КПД зацепления, рассчитан­ный по формулам (7.1) и (7.2) при различных соотношениях между и , то можно установить следующее:

– при , т.е. при отсутствии трения, КПД по обеим формулам по­лучается равным единице, что полностью закономерно;

– КПД по формуле (7.1) с увеличением угла примерно до 40° (точ­нее до ) увеличивается, а затем уменьшается, как пока­зано на рисунке 7.8. При этом, разумеется, для всех углов КПД тем выше, чем меньше или, иными словами, чем меньше коэффици­ент трения.

Заметим, что в реальных передачах угол далеко не дости­гает 40°. Ведь а при максимальном для стандартной передачи числе заходов и минимальном получаем Это соответствует

– КПД по формуле (7.1) может быть теоретически сколь угодно малым, но он всегда остается большим нуля;

– для передачи с ведущим червячным колесом КПД зацепления по формуле (7.2) при обращается в нуль. Этот случай проявляется в том, что передача движения от колеса к червяку ока­зыва­ется невозможной. Такую передачу именуют самотормозящей. Само­тормозящую передачу, при попытке вращения за колесо, можно сло­мать, но повернуть нельзя.

Свойство самоторможения червячных передач используется в тех­нике, чаще всего в грузоподъёмных машинах и механизмах. Оно позво­ляет упростить эти машины, отказавшись от тормозов, препятствующих обратному вращению под воздействием веса груза.

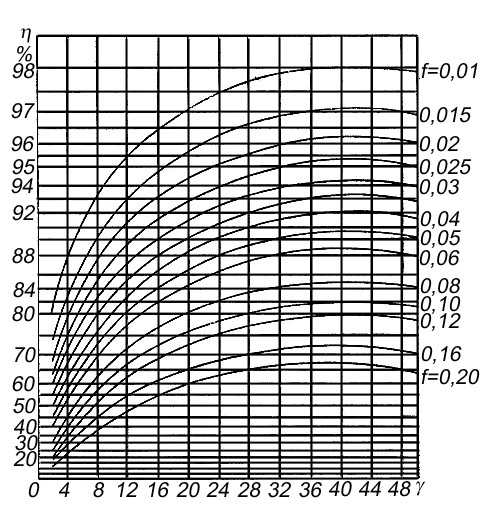
Рисунок 7.8 − Зависимость КПД червячного зацепления при веду­щем червяке от угла подъёма линии витка червяк для разных значе­ний коэффициента трения

Свойство самоторможения проявляется при . Если в фор­мулу (7.1) для КПД червячного зацепления при ведущем червяке под­ставить , то получим

.

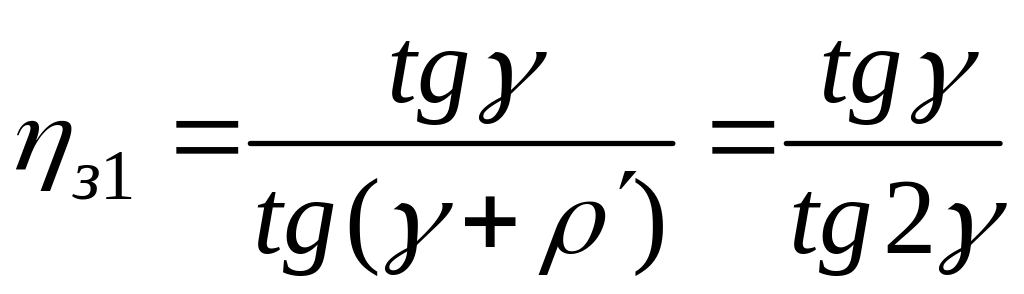Воспользовавшись известной из тригонометрии зависимостью

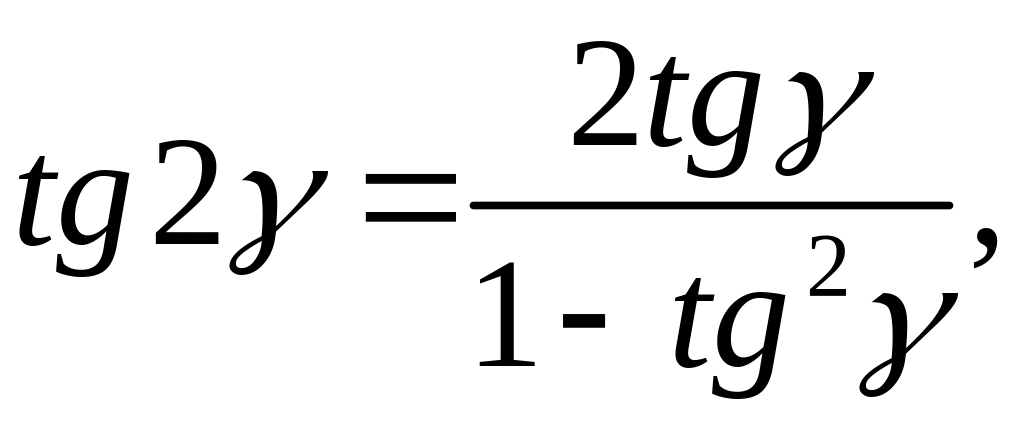
далее получим

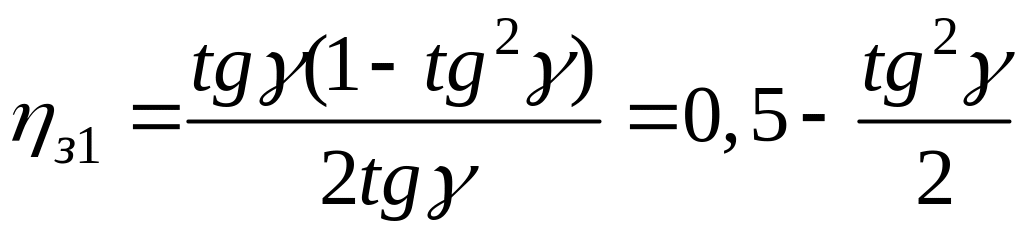. (7.3)

Таким образом, получается, что самотормозящая передача при ве­дущем червяке имеет КПД зацепления всегда меньше 0,5. А ведь КПД передачи в целом ещё меньше, так как в ней есть и другие потери, кроме потерь в зацеплении (см. формулу (2.7)). Такова цена применения самотормозящих передач в технике.