14. Формула прямоугольников

Дана непрерывная функция на отрезке [a,b]. Требуется вычислить определенный интеграл Разделим отрезок на n равных частей длины точками Обозначим через значения f(x) в этих точках,т.е.

Составим суммы:

Каждая из этих сумм – интегральная сумма для f(x) на отрезке [a,b] и поэтому приближенно вычисляет интеграл.

или

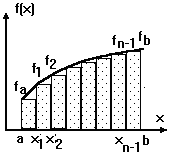
Суть метода прямоугольников для отрезка [a,b] проиллюстрирована на рисунке, при этом площадь под кривой f(x) заменена суммой площадей заштрихованных прямоугольников.

Примечание. Чем больше число шагов n, тем незначительнее ошибка при вычислении интеграла.

15.Формула трапеций.

Эта формула является более точной по сравнению с формулой прямоугольников, что объясняется заменой ступенчатой линии на вписанную ломаную.

y₁ у₂ у_n

a x₁ x₂ b x

Геометрически площадь криволинейной трапеции заменяется суммой площадей вписанных трапеций.

Площади вписанных трапеций вычисляются по формулам:

После приведения подобных слагаемых получаем формулу трапеций:

Число n выбирается произвольно. Чем больше оно будет, тем меньше будет шаг тем с большей точностью вычисляется значение интеграла.

Выбор числа шагов при заданной точности.

Вычислить приближенное значение с заданной точностью означает, что выполняется неравенство: - приближенное значение, - заданная погрешность.

При вычислениях интеграла погрешность учитывается следующим образом: М – наибольшее значение модуля второй производной на заданном отрезке.

13. Методы рационализации.

1. Подстановка Эйлера.

Рассмотрим интеграл где .Такой интеграл приводится к интегралу от рациональной функции нового переменного с помощью следующих подстановок Эйлера.

Первая подстановка Эйлера.

Если a>0, то полагаем:

Возьмем для определенности знак +. Получаем , откуда

, т.е. оказывается рациональной функцией от t. Так как ,x,dx выражаются рационально через t,то преобразуется в интеграл от рациональной функции от t.

Вторая подстановка Эйлера.

Если с>0, то полагаем: Берем для определенности знак +. . Отсюда .Т.к. dx и тоже выражаются рационально через t то, подставляя значения х, и dx в интеграл мы сведем его к интегралу от рациональной функции от t.

Третья подстановка Эйлера.

Пусть и – действительные корни трехчлена .Полагаем: = Так как = ,то Отсюда .Т.к. dx и тоже рационально зависят от t, то данный интеграл преобразуется в интеграл от рациональной функции от t.

Замечание1. Третья подстановка Э.применима не только при а<0,но и при a>0-лишь бы многочлен имел 2 действительных корня.

Замечание 2. Заметим, что для приведения интеграла к интегралу от рациональной функции достаточно первой и третьей подстановок Э. Рассмотрим трехчлен .Если ,то корни трехчлена действительны, и применима 3 подстановка Эйлера. Если , то в этом случае и, трехчлен имеет знак, совпадающий со знаком a. Чтобы был действительным, нужно, чтобы 3член был положительным, a>0.В этом случае применима первая подстановка.