2. Определенный интеграл.

Определенный интеграл. Если при любых разбиениях отрезка [a,b] таких, что и при любом выборе точек на отрезках [хi-1, xi] интегральная сумма стремится к одному и тому же пределу S, то этот предел называют определенным интегралом от функции f(x) на отрезке [a,b]и обозначают

Число а – нижний предел, число b – верхний предел. Отрезок [a,b] – отрезок интегрирования, х – переменная интегрирования.

Функция называется интегрируемой на отрезке [a,b], если для функции f(x) существует предел

Если построить график подынтегральной функции y=f(x), то в случае интеграл будет численно равен площади криволинейной трапеции, ограниченной прямыми х=а, х=b и осью Ох. В этом и заключается геометрический смысл.

Примечание автора. Обязательна графическая иллюстрация.

Физические задачи, решаемые с помощью определенного интеграла.

С помощью определенных интегралов решаются задачи на нахождение работы, скорости, пути, моментов инерции. Это осуществляется путем нахождения площадей, длин дуг, объемов и пр.

3. Теорема существования определенного интеграла. Если функция кусочно-непрерывна на отрезке [a,b], то она интегрируема на этом отрезке.

Примечание автора. В методическом пособии теорема приведена без доказательства.

Свойства определенного интеграла.

Свойство1. Постоянный множитель можно выносить за знак определенного интеграла: если А=const, то

Доказательство.

Свойство2. Определенный интеграл от алгебраической суммы нескольких функций равен алгебраической сумме интегралов от слагаемых.

Доказательство.

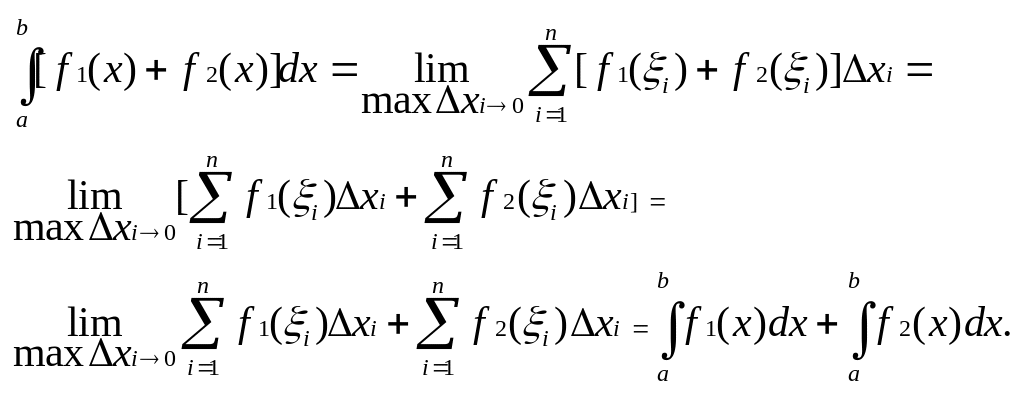
Свойство3. Если на отрезке [a,b], где а<b, функции f(x) и (х) удовлетворяют условию то

Доказательство. Рассмотрим разность

Каждая разность

Сл-но, неотрицательно каждое слагаемое, неотрицательны вся сумма и весь предел.

Свойство4. Если m и М – наименьшее и наибольшее значения функции f(x) на отрезке [a,b] и то

Доказательство. По условию

Подставляя 2 последние выражения в неравенство получаем исходное неравенство.

Свойство5 (теорема о среднем). Если функция f(x) непрерывна на отрезке [a,b], то на этом отрезке найдется такая точка что справедливо равенство:

Доказательство. Пусть a<b, m – наименьшее значение функции, М – наибольшее значение f(x) на отрезке [a,b]. Тогда получаем

Отсюда где

Так как функция непрерывна на отрезке, то она принимает все промежуточные значения, заключенные между m и М. Следовательно, при некотором значении будет то есть

Примечание автора. Доказательство приведено и в одном из следующих вопросов.

Свойство6. Для любых трех чисел a,b,c справедливо равенство если все эти три интеграла существуют.

Доказательство. Допустим сначала, что и составим интегральную сумму для функции f(x) на отрезке [a,b].

Так как предел интегральной суммы не зависит от способа разбиения отрезка, будем разбивать отрезок так, чтобы точка с была точкой деления. Тогда

Переходя к пределу при получим исходное соотношение.

Если на основании доказанного или

Поэтому имеем

Аналогично доказывается это свойство при любом взаимном расположении трех точек.