
- •В.В. Киричевський, н.М. Д’яченко інтегральне числення
- •6.050100 „Економічна кібернетика”
- •1. Неозначений інтеграл
- •1.1. Первісна і неозначений інтеграл
- •1.1.1. Основні властивості неозначеного інтегралу.
- •1.1.2. Таблиця основних інтегралів.
- •1.2. Основні методи інтегрування
- •1.2.1. Безпосереднє інтегрування.
- •1.2.2. Метод підстановки.
- •1.2.2.1. Частковий випадок: метод інтегрування внесення під диференціал.
- •1.2.2.2. Загальний випадок.
- •1.2.3. Інтегрування частинами.
- •1.3. Інтегрування раціональних функцій
- •1.4. Інтегрування тригонометричних функцій
- •1.5. Інтегрування ірраціональних функцій
- •2. Означений інтеграл
- •Поняття означеного інтегралу Римана та його властивості. Геометричний зміст означеного інтегралу
- •2.2. Економічний зміст означеного інтегралу
- •2.3. Обчислення означених інтегралів.
- •3. Застосування означеного інтегралу
- •3.1. Застосування означеного інтегралу в геометрії
- •3.1.1. Обчислення площ плоских фігур.
- •3.1.2. Обчислення довжин плоских дуг
- •3.1.3. Обчислення об’ємів тіл обертання
- •3.2. Застосування означеного інтегралу в економіці
- •4. Невласні інтеграли
- •5. Узагальнення поняття інтегралу
- •5.1. Визначення подвійного інтегралу та його властивості
- •5.2. Обчислення подвійних інтегралів
- •5.3. Геометричний зміст подвійного інтегралу
- •Типове індивідуальне завдання
- •Список літератури
- •Питання, що виносяться на самостійне вивчення
- •Питання, що виносяться на іспит і на колоквіум
- •Інтегральне числення
- •6.050100 „Економічна кібернетика”
1.4. Інтегрування тригонометричних функцій
Оскільки кожна раціональна функція інтегрується в елементарних функціях, то уведення заміни під знаком інтегралу, яке перетворює підінтегральну функцію в раціональну (раціоналізуючої заміни), дозволяє стверджувати, що відповідний інтеграл інтегрується в елементарних функціях.
Інтеграл
виду
|
завжди раціоналізується універсальною тригонометричною підстановкою
 ,
після уведення якої отримаємо
,
після уведення якої отримаємо
![]() ,
,
![]() ,
,
![]() ,
,
тому
![]() .
.
Недоліком наведеної підстановки є громіздкість отримуваних раціональних функцій у багатьох випадках. Саме тому розглянемо заміни, що призводять до більш зручних щодо інтегрування раціональних функцій.
Якщо
 ,
то уводять заміну
,
то уводять заміну
 .
.Якщо
 ,
то уводять заміну
,
то уводять заміну
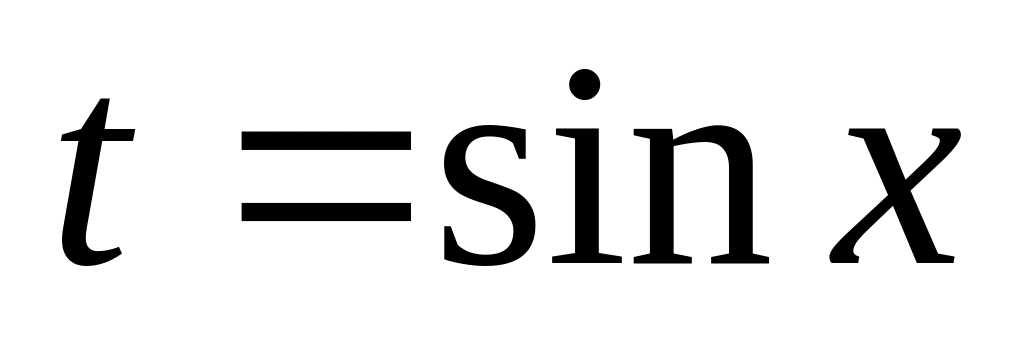 .
.Якщо
 ,
то уводять заміну
,
то уводять заміну
 .
.
Наведемо відповідні приклади.
У наступному прикладі використовується універсальна тригонометрична заміна

![]()
 .
.
Підінтегральна функція в інтегралі
 є непарною відносно синуса, тому зручно
застосовувати другу з наведених замін
є непарною відносно синуса, тому зручно
застосовувати другу з наведених замін
![]()
![]()
![]()
![]() .
.
3. Наступний приклад стосується заміни 4.
![]()
![]()
![]()
![]()
![]() .
.
Інтеграли
виду
|
4.
![]()
![]() .
.
5. Використовуємо формули зниження ступеня
![]()
![]() .
.
Для
інтегрування першої з функцій застосуємо
заміну
![]() ,
а саме:
,
а саме:
![]()
![]() ,
,
а для другої – формулу зниження ступеня
![]() ,
,
останні інтегруємо безпосередньо, тому разом одержимо
![]()
![]()
![]() .
.
1.5. Інтегрування ірраціональних функцій
Інтегрування дробово-лінійних ірраціональностей виду
|
Здійснюємо
підстановкою
![]() ,
звідки
,
звідки
![]() ,
,
![]() .
Ця підстановка раціоналізує підінтегральний
вираз.
.
Ця підстановка раціоналізує підінтегральний
вираз.
(№Д1932)

 .
.
Частковим
випадком дробово-лінійної ірраціональності
є функція
![]() .
.
(№Д1927) Для інтеграла
 у виразі дробово-лінійної
у виразі дробово-лінійної
ірраціональності
треба обрати
![]() ,
тоді після заміни
,
тоді після заміни
![]() отримаємо:
отримаємо:
![]() ,
,
![]()
![]()
![]() .
.
Метод
невизначених коефіцієнтів дає такі
результати:
![]() ,
тому
,
тому


![]()
![]() .
.
Інтегрування
квадратичних ірраціональностей
|
здійснюється підстановками Ейлера, які у даному випадку є універсальними:
перша
основна підстановка Ейлера
![]() ,
якщо
,
якщо
![]() ;
;
друга
основна підстановка Ейлера
![]() ;
;
третя
неосновна підстановка Ейлера
![]() .
.
(№Д1966)
![]()
![]()
![]() Інтегрування
підстановками Ейлера іноді призводить
до обчислення складних раціональних
функцій. Розглянемо один частковий
випадок, що дозволяє спростити таке
інтегрування.
Інтегрування
підстановками Ейлера іноді призводить
до обчислення складних раціональних
функцій. Розглянемо один частковий
випадок, що дозволяє спростити таке
інтегрування.
Інтегрування
квадратичних ірраціональностей виду
|
здійснюється представленням інтегралу у вигляді
![]() ,
,
де
![]() ‑ многочлен степеня
‑ многочлен степеня
![]() з невизначеними коефіцієнтами,
‑ невизначений коефіцієнт.
з невизначеними коефіцієнтами,
‑ невизначений коефіцієнт.
4.
(№Д1946) Обчислити інтеграл
![]() .
.
В чисельнику стоїть многочлен третього степеня, тому многочлен з невизначеними коефіцієнтами треба обрати другого степеня, і тоді отримаємо:
![]() .
.
Для отримання значень невизначених коефіцієнтів треба спочатку продиференціювати обидві частини останньої рівності:

потім
обидві частини помножаємо на квадратичну
ірраціональність
![]() :
:
![]() ,
,
після чого застосовуємо метод невизначених коефіцієнтів

Звідки отримаємо
![]()
![]()
Інтеграл
від диференціального біному
|
якщо
 - ціле, то покладають
- ціле, то покладають
 ,
де
,
де
 - спільний знаменник дробів
- спільний знаменник дробів
 і
;
і
;якщо
 - ціле, покладають
- ціле, покладають
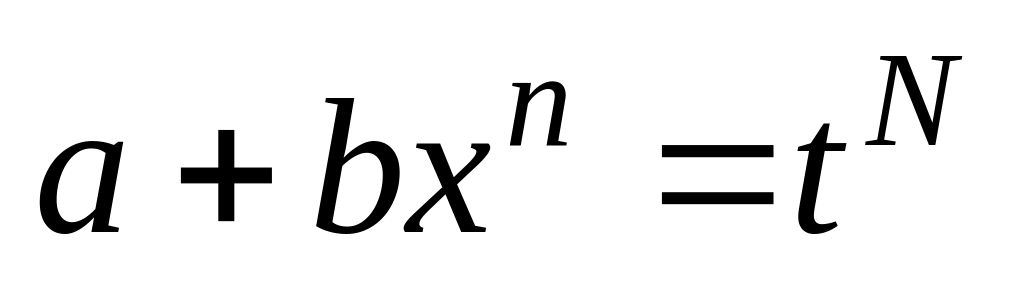 ,
де
- знаменник дробу
;
,
де
- знаменник дробу
;якщо
 - ціле, покладають
- ціле, покладають
 ,
де
- знаменник дробу
.
,
де
- знаменник дробу
.
5. (№Д1987)
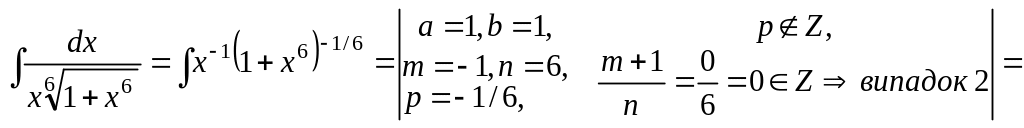

![]()
![]()
![]()
![]()
![]()
![]() .
.
