
- •В.В. Киричевський, н.М. Д’яченко інтегральне числення
- •6.050100 „Економічна кібернетика”
- •1. Неозначений інтеграл
- •1.1. Первісна і неозначений інтеграл
- •1.1.1. Основні властивості неозначеного інтегралу.
- •1.1.2. Таблиця основних інтегралів.
- •1.2. Основні методи інтегрування
- •1.2.1. Безпосереднє інтегрування.
- •1.2.2. Метод підстановки.
- •1.2.2.1. Частковий випадок: метод інтегрування внесення під диференціал.
- •1.2.2.2. Загальний випадок.
- •1.2.3. Інтегрування частинами.
- •1.3. Інтегрування раціональних функцій
- •1.4. Інтегрування тригонометричних функцій
- •1.5. Інтегрування ірраціональних функцій
- •2. Означений інтеграл
- •Поняття означеного інтегралу Римана та його властивості. Геометричний зміст означеного інтегралу
- •2.2. Економічний зміст означеного інтегралу
- •2.3. Обчислення означених інтегралів.
- •3. Застосування означеного інтегралу
- •3.1. Застосування означеного інтегралу в геометрії
- •3.1.1. Обчислення площ плоских фігур.
- •3.1.2. Обчислення довжин плоских дуг
- •3.1.3. Обчислення об’ємів тіл обертання
- •3.2. Застосування означеного інтегралу в економіці
- •4. Невласні інтеграли
- •5. Узагальнення поняття інтегралу
- •5.1. Визначення подвійного інтегралу та його властивості
- •5.2. Обчислення подвійних інтегралів
- •5.3. Геометричний зміст подвійного інтегралу
- •Типове індивідуальне завдання
- •Список літератури
- •Питання, що виносяться на самостійне вивчення
- •Питання, що виносяться на іспит і на колоквіум
- •Інтегральне числення
- •6.050100 „Економічна кібернетика”
1. Неозначений інтеграл
1.1. Первісна і неозначений інтеграл
Нехай
множина
![]() є інтервалом
є інтервалом
![]() ,
променем
,
променем
![]() чи
чи
![]() або числовою прямою
або числовою прямою
![]() .
.
Визначення
1.1.
Функцію
![]() називають первісною
функції
називають первісною
функції
![]() на множині
,
якщо функція
диференційована на
і виконується співвідношення
на множині
,
якщо функція
диференційована на
і виконується співвідношення
![]() .
.
Теорема
1.1.
Якщо дві функції
![]() і
і
![]() – первісні функції
на множині
,
то
– первісні функції
на множині
,
то
![]()
![]() ,
де
,
де
![]() .
.
Визначення 1.2. Сукупність усіх первісних даної функції на множині називають неозначеним інтегралом функції на множині і позначають
![]() .
.
Функцію
називають підінтегральною,
а вираз
![]() - підінтегральним виразом. Якщо
- одна з первісних
на
,
то
- підінтегральним виразом. Якщо
- одна з первісних
на
,
то
![]() .
.
Останнє співвідношення слід розуміти як рівність між двома множинами.
1.1.1. Основні властивості неозначеного інтегралу.
![]()


![]()
![]()
![]() .
.
Властивості лінійності мають місце з точністю до константи.
1.1.2. Таблиця основних інтегралів.
Нехай
![]()
№пп |
|
|
№ пп |
|
|
|
1. |
|
|
|
|
|
|
2. |
|
|
3. |
|
|
|
4. |
|
|
5. |
|
|
|
6. |
|
|
7. |
|
|
|
8. |
|
|
9. |
|
|
|
10. |
|
|
11. |
|
|
|
12. |
|
|
13. |
|
|
|
14. |
|
|
15. |
|
|
|
16. |
|
|
17. |
|
||
18. |
|
|
||||
19. |
|
|
||||
1.2. Основні методи інтегрування
До основних методів інтегрування можна віднести
безпосереднє інтегрування,
метод підстановки (заміни), зокрема метод внесення під диференціал
метод інтегрування частинами.
1.2.1. Безпосереднє інтегрування.
Цей метод передбачає застосування таблиці і властивостей неозначеного інтегралу. Розглянемо приклади.
(№Д16381)

 .
.(№Д1670)






1.2.2. Метод підстановки.
Теорема
1.2.
Якщо функція
![]() визначена і диференційована на множині
і має множину визначення
визначена і диференційована на множині
і має множину визначення
![]() ,
а для функції
,
а для функції
![]() на множині
на множині
![]() існує первісна
існує первісна
![]() ,
тобто
,
тобто
![]() ,
тоді на
функція
,
тоді на
функція
![]() має первісну, що дорівнює
має первісну, що дорівнює
![]() ,
тобто
,
тобто
![]() .
.
1.2.2.1. Частковий випадок: метод інтегрування внесення під диференціал.
Розглянемо приклади
(№Д1675)

 .
.(№Д1679)
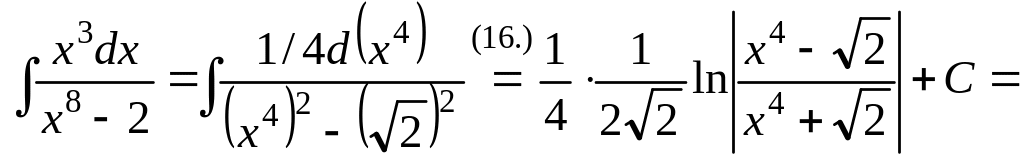
 .
.(№1697)
 .
.(№Д1704)

 .
.
Наступний інтеграл відноситься до найпростіших і інтегрується методами внесення під диференціал і методом безпосереднього інтегрування.
Інтеграли
виду
|

Перший з отриманих інтегралів береться занесенням під диференціал, а другий ‑ виділенням повного квадрату:

Відповідь
буде залежати від
![]() .
Розглянемо приклад.
.
Розглянемо приклад.
(№Д1852)
![]()
![]()

![]()
![]()
![]() .
.


