
- •В.В. Киричевський, н.М. Д’яченко інтегральне числення
- •6.050100 „Економічна кібернетика”
- •1. Неозначений інтеграл
- •1.1. Первісна і неозначений інтеграл
- •1.1.1. Основні властивості неозначеного інтегралу.
- •1.1.2. Таблиця основних інтегралів.
- •1.2. Основні методи інтегрування
- •1.2.1. Безпосереднє інтегрування.
- •1.2.2. Метод підстановки.
- •1.2.2.1. Частковий випадок: метод інтегрування внесення під диференціал.
- •1.2.2.2. Загальний випадок.
- •1.2.3. Інтегрування частинами.
- •1.3. Інтегрування раціональних функцій
- •1.4. Інтегрування тригонометричних функцій
- •1.5. Інтегрування ірраціональних функцій
- •2. Означений інтеграл
- •Поняття означеного інтегралу Римана та його властивості. Геометричний зміст означеного інтегралу
- •2.2. Економічний зміст означеного інтегралу
- •2.3. Обчислення означених інтегралів.
- •3. Застосування означеного інтегралу
- •3.1. Застосування означеного інтегралу в геометрії
- •3.1.1. Обчислення площ плоских фігур.
- •3.1.2. Обчислення довжин плоских дуг
- •3.1.3. Обчислення об’ємів тіл обертання
- •3.2. Застосування означеного інтегралу в економіці
- •4. Невласні інтеграли
- •5. Узагальнення поняття інтегралу
- •5.1. Визначення подвійного інтегралу та його властивості
- •5.2. Обчислення подвійних інтегралів
- •5.3. Геометричний зміст подвійного інтегралу
- •Типове індивідуальне завдання
- •Список літератури
- •Питання, що виносяться на самостійне вивчення
- •Питання, що виносяться на іспит і на колоквіум
- •Інтегральне числення
- •6.050100 „Економічна кібернетика”
5.3. Геометричний зміст подвійного інтегралу
Я
Рис. 5.4.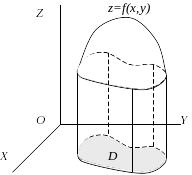
![]() (див. рис. 5.4). Якщо
=1
для усіх
(див. рис. 5.4). Якщо
=1
для усіх
![]() ,
то
,
то
![]() чисельно дорівнює площі області
,
тобто
чисельно дорівнює площі області
,
тобто
![]() .
.
1. Обчислити площі плоских фігур, що обмежені лініями
а)
![]() ,
,
б)
![]() .
.
а) Дані
дві параболи читачеві пропонується
зобразити самостійно. Координати точок
перетину цих парабол є розв’язками
системи рівнянь
![]() ,
тобто
,
тобто
![]() .
У даному випадку в якості зовнішньої
межі інтегрування простіше обрати
.
Області
відповідають такі зміни
і
:
.
У даному випадку в якості зовнішньої
межі інтегрування простіше обрати
.
Області
відповідають такі зміни
і
:
![]() ,
,
![]() ,
Вважаючи на геометричний зміст подвійного
інтегралу, отримаємо:
,
Вважаючи на геометричний зміст подвійного
інтегралу, отримаємо:
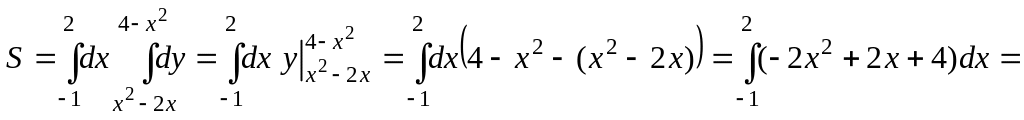
![]() .
.
б) Уведемо
полярні координати
,
тоді
,
а рівняння кривої, що обмежує область
придбає вигляд:
![]() ,
тобто
,
тобто
![]() .
Межі зміни полярного кута знайдемо із
нерівності
.
Межі зміни полярного кута знайдемо із
нерівності
![]() ,
тобто
,
тобто
![]() .
На відрізку
.
На відрізку
![]() ця нерівність має розв’язок
ця нерівність має розв’язок
![]() ,
тому
,
тому
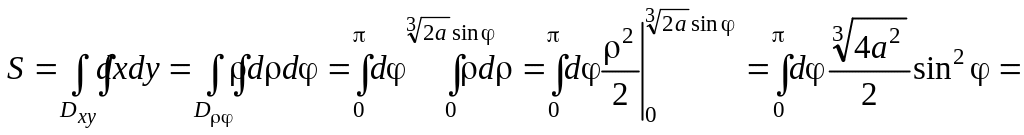
![]() .
.
2. Обчислити об’єм тіла, що обмежено поверхнями
а)
![]()
![]() ,
,
б)
![]() .
.
а
Рис. 5.5.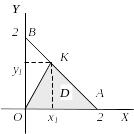
![]() відсікає піраміду, а на площині xOy
‑ трикутник ОАВ
прямою
відсікає піраміду, а на площині xOy
‑ трикутник ОАВ
прямою
![]() ,
тобто
,
тобто
![]() .
Площина
.
Площина
![]() ділить піраміду на дві піраміди, а
трикутник ОАВ
‑ на два
трикутники ОКВ
і ОКА, які
є проекціями створених пірамід. Оскільки
не зазначено, об’єм якої саме піраміди
потрібно знайти, знайдемо об’єми обох.
ділить піраміду на дві піраміди, а
трикутник ОАВ
‑ на два
трикутники ОКВ
і ОКА, які
є проекціями створених пірамід. Оскільки
не зазначено, об’єм якої саме піраміди
потрібно знайти, знайдемо об’єми обох.
Знайдемо
координати точки К,
що є точкою перетину прямих
і
.
Для цього розв’яжемо систему
![]() ,
звідки отримаємо
,
звідки отримаємо
![]() .
.
Виходячи
з геометричного змісту подвійного
інтегралу, знайдемо об’єм піраміди з
основою ОКА:
![]() .
Даний інтеграл простіше обчислити,
обравши зовнішньою межею інтегрування
y.
В рівняннях прямих х
виразимо через у,
одержимо:
.
Даний інтеграл простіше обчислити,
обравши зовнішньою межею інтегрування
y.
В рівняннях прямих х
виразимо через у,
одержимо:
![]() ,
а інтеграл придбає вигляд:
,
а інтеграл придбає вигляд:
![]()
EMBED Equation.3
![]()
![]()
Об’єм
піраміди з основою ОКВ
можна знайти за допомогою подвійного
інтегралу, а можна і з розумінь аналітичної
геометрії. Об’єм усієї піраміди, що
відсікається площиною
![]() дорівнює
дорівнює
![]() ,
тому шуканий об’єм дорівнює
,
тому шуканий об’єм дорівнює
![]() .
.
б
Рис. 5.6.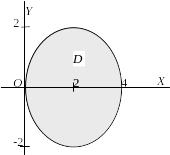
![]() є циліндричною з твірною, що паралельна
вісі Оу.
Вона відсікає на площині хОу
півплощину
є циліндричною з твірною, що паралельна
вісі Оу.
Вона відсікає на площині хОу
півплощину
![]() .
Рівняння поверхні
.
Рівняння поверхні
![]() можна переписати, виділивши повний
квадрат, у вигляді
можна переписати, виділивши повний
квадрат, у вигляді
![]() .
Звідси зрозуміло, що ця поверхня є
круговим циліндром. В проекції на хОу
цей циліндр утворює коло з центром в
точці (2; 0) радіусу 2, яке цілком міститься
в середині півплощини
.
Тому проекцією даного тіла на площину
хОу
є круг, який обмежує зазначене коло
(рис. 5.6).
.
Звідси зрозуміло, що ця поверхня є
круговим циліндром. В проекції на хОу
цей циліндр утворює коло з центром в
точці (2; 0) радіусу 2, яке цілком міститься
в середині півплощини
.
Тому проекцією даного тіла на площину
хОу
є круг, який обмежує зазначене коло
(рис. 5.6).
Об’єм
даного тіла обчислюється за формулою
![]() .
В рівнянні кола виражаємо
.
В рівнянні кола виражаємо
![]() через
:
через
:
![]() ,
де знак „+” відповідає верхній частині
кола, а „‑” – нижній. Область
характеризується такою зміною координат:
,
де знак „+” відповідає верхній частині
кола, а „‑” – нижній. Область
характеризується такою зміною координат:
![]() ,
тому одержуємо:
,
тому одержуємо:
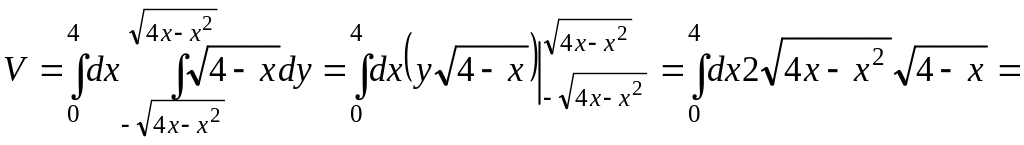
![]()
Типове індивідуальне завдання
Варіант 1. |
|
|||||
1.1. безпосереднім інтегруванням або внесенням під диференціал |
|
|||||
a)
|
а) |
б) |
||||
б) |
в) |
в)
|
г) |
|||
г)
|
д) |
д)
|
||||
1.3. методом інтегруванням частинами |
1.4. від тригонометричних функцій |
|||||
а)
|
б)
|
а) |
|
|||
в)
|
г)
|
б) |
в)
|
|||
д)
|
г) |
д)
|
||||
1.5. від дробово-раціональних функцій |
|
|||||
а) |
б) |
а)
|
||||
в)
|
б)
|
|||||
1.7. від ірраціональних функцій |
1.8. за допомогою тригонометричної підстановки |
|||||
а)
|
б) |
а)
|
||||
|
|
|||||
a)
|
б) |
а)
|
б) |
|||
в) |
в)
|
|
||||
|
а) |
|||||
а)
|
б)
|
|||||
в)
|
б)
|
|||||
6.
Обчислити наступний невласний інтеграл
(або встановити його розбіжність)
|
7.
Представити подвійний інтеграл
|
|||||
8. Обчислити подвійний інтеграл
|
||||||
9. Обчислити подвійний інтеграл, використавши полярні координати |
10. Обчислити об’єм тіла, що обмежено поверхнями |
|||||
|
|
|||||
Варіант 2. |
|
|||||
1.1. безпосереднім інтегруванням або внесенням під диференціал |
|
|||||
a)
;
|
а)
|
б) |
||||
б) |
в) |
в)
|
г) |
|||
г)
|
д) |
д)
|
||||
1.3. методом інтегруванням частинами |
1.4. від тригонометричних функцій |
|||||
а)
|
б)
|
а) |
|
|||
в) |
г) |
б) |
в)
|
|||
д)
|
г) |
д)
|
||||
1.5. від дробово-раціональних функцій |
|
|||||
а) |
б) |
а)
|
||||
в)
|
б)
|
|||||
1.7. від ірраціональних функцій |
1.8. за допомогою тригонометричної підстановки |
|||||
а)
|
б) |
а) |
||||
|
|
|||||
a)
|
б) |
а) |
б) |
|||
в) |
в)
|
|
||||
|
а) |
|||||
а)
|
б)
|
|||||
в)
|
б)
|
|||||
6.
Обчислити наступний невласний інтеграл
(або встановити його розбіжність)
|
7.
Представити подвійний інтеграл
у вигляді повторного інтеграла з
зовнішнім інтегруванням за
та зовнішнім інтегруванням за
,
якщо область
задана указаними лініями
|
|||||
8. Обчислити подвійний інтеграл
|
||||||
9. Обчислити подвійний інтеграл, використавши полярні координати |
10. Обчислити об’єм тіла, що обмежено поверхнями |
|||||
|
|
|||||
Варіант 3. |
|
|||
1.1. безпосереднім інтегруванням або внесенням під диференціал |
|
|||
a)
;
|
а)
|
б) |
||
б) |
в) |
в)
|
г) |
|
г)
|
д) |
д)
|
||
1.3. методом інтегруванням частинами |
1.4. від тригонометричних функцій |
|||
а)
|
б)
|
а) |
|
|
в) |
г) |
б) |
в)
|
|
д)
|
г) |
д)
|
||
1.5. від дробово-раціональних функцій |
|
|||
а) |
б) |
а)
|
||
в) |
б)
|
|||
1.7. від ірраціональних функцій |
1.8. за допомогою тригонометричної підстановки |
|||
а)
|
б) |
а) |
||
|
|
|||
a)
|
б) |
а)
|
б) |
|
в) |
в)
|
|||
|
а) |
|||
а)
|
б)
|
|||
в)
|
б)
|
|||
6.
Обчислити наступний невласний інтеграл
(або встановити його розбіжність)
|
7.
Представити подвійний інтеграл
у вигляді повторного інтеграла з
зовнішнім інтегруванням за
та зовнішнім інтегруванням за
,
якщо область
задана указаними лініями
|
|||
8. Обчислити подвійний інтеграл
|
||||
9. Обчислити подвійний інтеграл, використавши полярні координати |
10. Обчислити об’єм тіла, що обмежено поверхнями |
|||
|
|
|||
Варіант 4. |
|
|||||
1.1. безпосереднім інтегруванням або внесенням під диференціал |
|
|||||
a) |
б) |
а)
|
б) |
|||
в) |
д) |
в)
|
г) |
|||
г)
|
д)
|
|||||
1.3. методом інтегруванням частинами |
1.4. від тригонометричних функцій |
|||||
а)
|
б)
|
а) |
|
|||
в) |
г) |
б) |
в)
|
|||
д)
|
г) |
д)
|
||||
1.5. від дробово-раціональних функцій |
|
|||||
а) |
б) |
а)
|
||||
в) |
б)
|
|||||
1.7. від ірраціональних функцій |
1.8. за допомогою тригонометричної підстановки |
|||||
а)
|
б) |
а) |
||||
|
|
|||||
a)
|
б) |
а) |
б) |
|||
в) |
в)
|
|||||
|
а) |
|||||
а)
|
б)
|
|||||
в)
|
б)
|
|||||
6.
Обчислити наступний невласний інтеграл
(або встановити його розбіжність)
|
7.
Представити подвійний інтеграл
у вигляді повторного інтеграла з
зовнішнім інтегруванням за
та зовнішнім інтегруванням за
,
якщо область
задана указаними лініями
|
|||||
8. Обчислити подвійний інтеграл
|
||||||
9. Обчислити подвійний інтеграл, використавши полярні координати |
10. Обчислити об’єм тіла, що обмежено поверхнями |
|||||
|
|
|||||
Варіант 5. |
|
|||||
1.1. безпосереднім інтегруванням або внесенням під диференціал |
|
|||||
a)
|
б) |
а) |
б) |
|||
в) |
г)
|
в)
|
г) |
|||
д) |
|
д) |
||||
1.3. методом інтегруванням частинами |
1.4. від тригонометричних функцій |
|||||
а)
|
б) ; |
а) |
||||
в)
|
г)
|
б) |
в)
|
|||
д)
|
г) |
д)
|
||||
1.5. від дробово-раціональних функцій |
|
|||||
а) |
б) |
а)
|
||||
в)
|
б)
|
|||||
1.7. від ірраціональних функцій |
1.8. за допомогою тригонометричної підстановки |
|||||
а)
|
б) |
а)
|
||||
|
|
|||||
a)
|
б) |
а)
|
б) |
|||
в) |
в)
|
|||||
|
а) |
|||||
а)
|
б)
|
|||||
в)
|
б)
|
|||||
6.
Обчислити наступний невласний інтеграл
(або встановити його розбіжність)
|
7.
Представити подвійний інтеграл
у вигляді повторного інтеграла з
зовнішнім інтегруванням за
та зовнішнім інтегруванням за
,
якщо область
задана указаними лініями
|
|||||
8. Обчислити подвійний інтеграл
|
||||||
9. Обчислити подвійний інтеграл, використавши полярні координати |
10. Обчислити об’єм тіла, що обмежено поверхнями |
|||||
|
|
|||||
Варіант 6. |
|
|||||||
1.1. безпосереднім інтегруванням або внесенням під диференціал |
|
|||||||
a)
;
|
б) |
а)
|
б) |
|||||
в) |
г)
|
в)
|
г) |
|||||
д) |
|
д)
|
||||||
1.3. методом інтегруванням частинами |
1.4. від тригонометричних функцій |
|||||||
а)
|
б)
|
а) |
|
|||||
в) |
г) |
б) |
в)
|
|||||
д)
|
г) |
д)
|
||||||
1.5. від дробово-раціональних функцій |
|
|||||||
а) |
б) |
а)
|
||||||
в) ; |
б)
|
|||||||
1.7. від ірраціональних функцій |
1.8. за допомогою тригонометричної підстановки |
|||||||
а) |
б); |
а) |
||||||
|
|
|||||||
a) |
б); |
а) |
|
|||||
в) |
в)
|
|
||||||
|
а) |
|||||||
а)
|
б)
|
|||||||
в)
|
б)
|
|||||||
6.
Обчислити наступний невласний інтеграл
(або встановити його розбіжність)
|
7.
Представити подвійний інтеграл
у вигляді повторного інтеграла з
зовнішнім інтегруванням за
та зовнішнім інтегруванням за
,
якщо область
задана указаними лініями
|
|||||||
8. Обчислити подвійний інтеграл
|
||||||||
9. Обчислити подвійний інтеграл, використавши полярні координати |
10. Обчислити об’єм тіла, що обмежено поверхнями |
|||||||
|
|
|||||||
Варіант 7. |
|
||||||||
1.1. безпосереднім інтегруванням або внесенням під диференціал |
|
||||||||
a)
;
|
б) |
а)
|
б) |
||||||
в) |
д) |
в)
|
г) |
||||||
г)
|
д)
|
||||||||
1.3. методом інтегруванням частинами |
1.4. від тригонометричних функцій |
||||||||
а)
|
б)
|
а) |
|
||||||
в) |
г) |
б) |
в)
|
||||||
д)
|
г) |
д)
|
|||||||
1.5. від дробово-раціональних функцій |
|
||||||||
а) |
б) |
а)
|
|||||||
в)
|
б)
|
||||||||
1.7. від ірраціональних функцій |
1.8. за допомогою тригонометричної підстановки |
||||||||
а) |
б); |
а) |
|||||||
|
|
||||||||
a) |
б); |
а) |
б) |
||||||
в) |
в)
|
|
|||||||
|
а) |
||||||||
а)
|
б)
|
||||||||
в)
|
б)
|
||||||||
6.
Обчислити наступний невласний інтеграл
(або встановити його розбіжність)
|
7.
Представити подвійний інтеграл
у вигляді повторного інтеграла з
зовнішнім інтегруванням за
та зовнішнім інтегруванням за
,
якщо область
задана указаними лініями
|
||||||||
8. Обчислити подвійний інтеграл
|
|||||||||
9. Обчислити подвійний інтеграл, використавши полярні координати |
10. Обчислити об’єм тіла, що обмежено поверхнями |
||||||||
|
|
||||||||
|
|
||||||||
Варіант 8. |
|
||||||||
1.1. безпосереднім інтегруванням або внесенням під диференціал |
|
||||||||
a)
|
а) |
б) |
|||||||
б) |
в) |
в)
|
г) |
||||||
г)
|
д) |
д)
|
|||||||
1.3. методом інтегруванням частинами |
1.4. від тригонометричних функцій |
||||||||
а)
|
б)
|
а) |
|
||||||
в)
|
г)
|
б) |
в)
|
||||||
д)
|
г) |
д)
|
|||||||
1.5. від дробово-раціональних функцій |
|
||||||||
а) |
б) |
а)
|
|||||||
в)
|
б)
|
||||||||
1.7. від ірраціональних функцій |
1.8. за допомогою тригонометричної підстановки |
||||||||
а)
|
б) |
а)
|
|||||||
|
|
||||||||
a)
|
б) |
а)
|
б) |
||||||
в) |
в)
|
|
|||||||
|
а) |
||||||||
а)
|
б) |
||||||||
в)
|
б) |
||||||||
6.
Обчислити наступний невласний інтеграл
(або встановити його розбіжність)
|
7.
Представити подвійний інтеграл
у вигляді повторного інтеграла з
зовнішнім інтегруванням за
та зовнішнім інтегруванням за
,
якщо область
задана указаними лініями
|
||||||||
8. Обчислити подвійний інтеграл
|
|||||||||
9. Обчислити подвійний інтеграл, використавши полярні координати |
10. Обчислити об’єм тіла, що обмежено поверхнями |
||||||||
|
|
||||||||
Варіант 9. |
|
|||||
1.1. безпосереднім інтегруванням або внесенням під диференціал |
|
|||||
a)
;
|
а)
|
б) |
||||
б) |
в) |
в)
|
г) |
|||
г)
|
д) |
д)
|
||||
1.3. методом інтегруванням частинами |
1.4. від тригонометричних функцій |
|||||
а)
|
б)
|
а) |
|
|||
в) |
г) |
б) |
в)
|
|||
д)
|
г) |
д) ; |
||||
1.5. від дробово-раціональних функцій |
|
|||||
а) |
б) |
а)
|
||||
в)
|
б)
|
|||||
1.7. від ірраціональних функцій |
1.8. за допомогою тригонометричної підстановки |
|||||
а)
|
б) |
а) |
||||
|
|
|||||
a)
|
б) |
а) |
б) |
|||
в) |
в)
|
|
||||
|
а) |
|||||
а)
|
б)
|
|||||
в)
|
б)
|
|||||
6.
Обчислити наступний невласний інтеграл
(або встановити його розбіжність)
|
7.
Представити подвійний інтеграл
у вигляді повторного інтеграла з
зовнішнім інтегруванням за
та зовнішнім інтегруванням за
,
якщо область
задана указаними лініями
|
|||||
8. Обчислити подвійний інтеграл
|
||||||
9. Обчислити подвійний інтеграл, використавши полярні координати |
10. Обчислити об’єм тіла, що обмежено поверхнями |
|||||
|
|
|||||
Варіант 10. |
|
||||
1.1. безпосереднім інтегруванням або внесенням під диференціал |
|
||||
a)
;
|
а) ; |
б) |
|||
б) |
в) |
в)
|
г) |
||
г)
|
д) |
д)
|
|||
1.3. методом інтегруванням частинами |
1.4. від тригонометричних функцій |
||||
а)
|
б)
|
а) |
|
||
в) |
г) |
б) |
в)
|
||
д)
|
г) |
д)
|
|||
1.5. від дробово-раціональних функцій |
|
||||
а) |
б) |
а)
|
|||
в) |
б)
|
||||
1.7. від ірраціональних функцій |
1.8. за допомогою тригонометричної підстановки |
||||
а)
|
б) |
а) |
|||
|
|
||||
a)
|
б) |
а)
|
б) |
||
в) |
в)
|
||||
|
а) ; |
||||
а) від до ; |
б) ; |
||||
в) . |
б) .
|
||||
6.
Обчислити наступний невласний інтеграл
(або встановити його розбіжність)
|
7.
Представити подвійний інтеграл
у вигляді повторного інтеграла з
зовнішнім інтегруванням за
та зовнішнім інтегруванням за
,
якщо область
задана указаними лініями
|
||||
8. Обчислити подвійний інтеграл
|
|||||
9. Обчислити подвійний інтеграл, використавши полярні координати |
10. Обчислити об’єм тіла, що обмежено поверхнями |
||||
|
|
||||
Варіант 11. |
|
||||||
1.1. безпосереднім інтегруванням або внесенням під диференціал |
|
||||||
a) |
б) |
а)
|
б) |
||||
в) |
д) |
в)
|
г) |
||||
г)
|
д)
|
||||||
1.3. методом інтегруванням частинами |
1.4. від тригонометричних функцій |
||||||
а)
|
б)
|
а) |
|
||||
в) |
г) |
б) |
в)
|
||||
д)
|
г) |
д)
|
|||||
1.5. від дробово-раціональних функцій |
|
||||||
а) |
б) |
а)
|
|||||
в) |
б)
|
||||||
1.7. від ірраціональних функцій |
1.8. за допомогою тригонометричної підстановки |
||||||
а)
|
б) |
а) |
|||||
|
|
||||||
a)
|
б) |
а) |
б) |
||||
в) |
в)
|
||||||
|
а) |
||||||
а)
|
б)
|
||||||
в) . |
б)
|
||||||
6.
Обчислити наступний невласний інтеграл
(або встановити його розбіжність)
|
7.
Представити подвійний інтеграл
у вигляді повторного інтеграла з
зовнішнім інтегруванням за
та зовнішнім інтегруванням за
,
якщо область
задана указаними лініями
|
||||||
8. Обчислити подвійний інтеграл
|
|||||||
9. Обчислити подвійний інтеграл, використавши полярні координати |
10. Обчислити об’єм тіла, що обмежено поверхнями |
||||||
|
|
||||||
Варіант 12. |
|
|||||
1.1. безпосереднім інтегруванням або внесенням під диференціал |
|
|||||
a)
|
б) |
а) |
б) |
|||
в) |
г)
|
в)
|
г) |
|||
д) |
|
д) |
||||
1.3. методом інтегруванням частинами |
1.4. від тригонометричних функцій |
|||||
а)
|
б) ; |
а) |
||||
в)
|
г)
|
б) |
в)
|
|||
д)
|
г) |
д) ; |
||||
1.5. від дробово-раціональних функцій |
|
|||||
а) |
б) |
а)
|
||||
в)
|
б)
|
|||||
1.7. від ірраціональних функцій |
1.8. за допомогою тригонометричної підстановки |
|||||
а)
|
б) |
а)
|
||||
|
|
|||||
a)
|
б) |
а)
|
б) |
|||
в) |
в)
|
|||||
|
а) |
|||||
а)
|
б)
|
|||||
в)
|
б)
|
|||||
6.
Обчислити наступний невласний інтеграл
(або встановити його розбіжність)
|
7.
Представити подвійний інтеграл
у вигляді повторного інтеграла з
зовнішнім інтегруванням за
та зовнішнім інтегруванням за
,
якщо область
задана указаними лініями
|
|||||
8. Обчислити подвійний інтеграл
|
||||||
9. Обчислити подвійний інтеграл, використавши полярні координати |
10. Обчислити об’єм тіла, що обмежено поверхнями |
|||||
|
|
|||||
Останні два
завдання (тут
![]() - номер групи,
- номер групи,
![]() - номер варіанта студента)
- номер варіанта студента)
11. За
функцією продуктивності праці
|
12. Чисті
інвестиції задані функцією
|

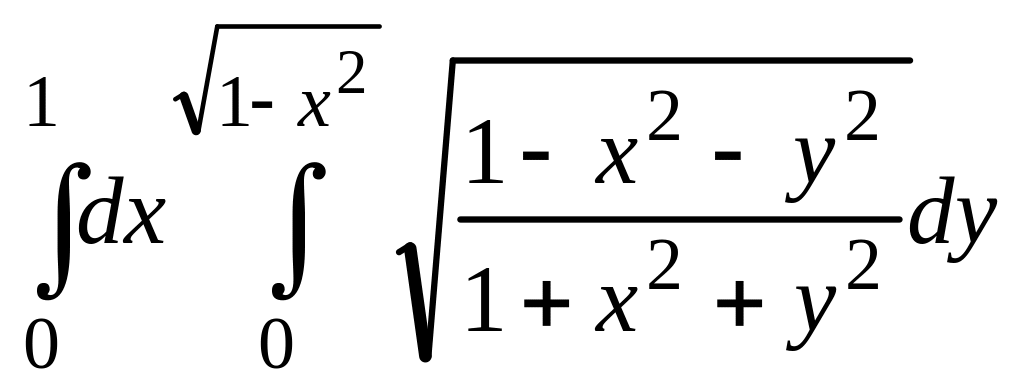


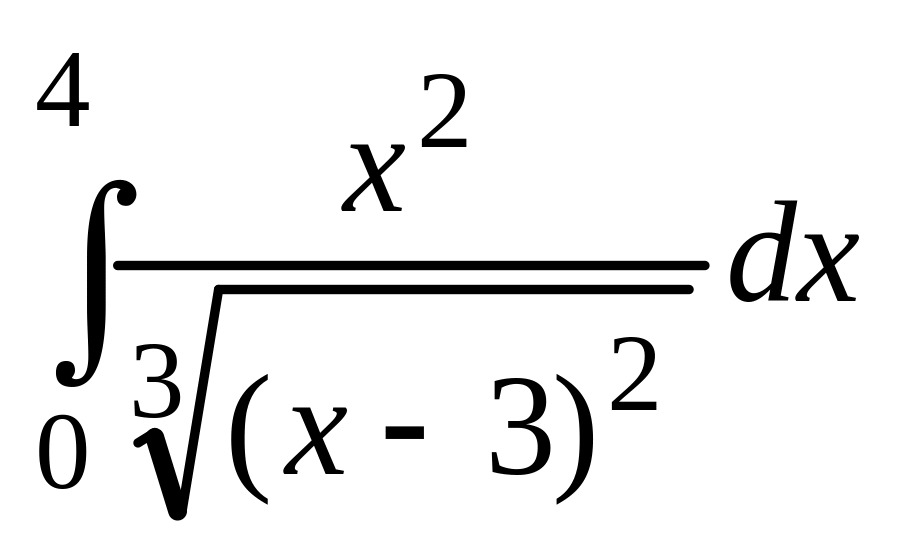


 ;
;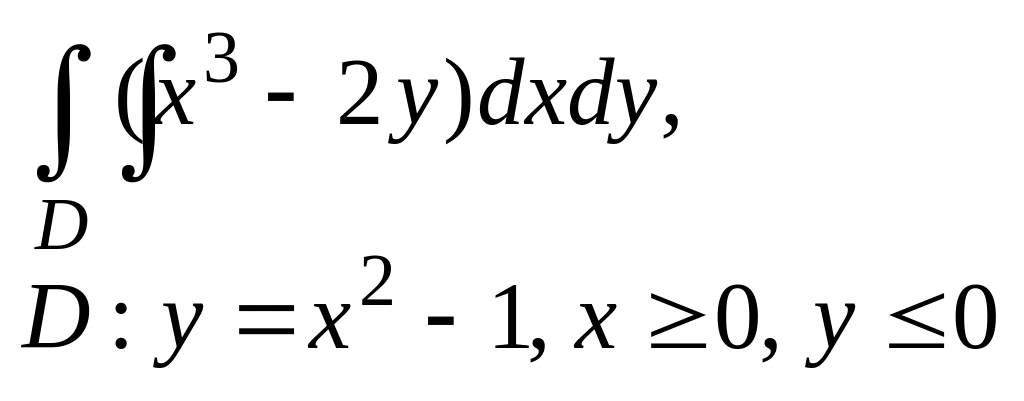
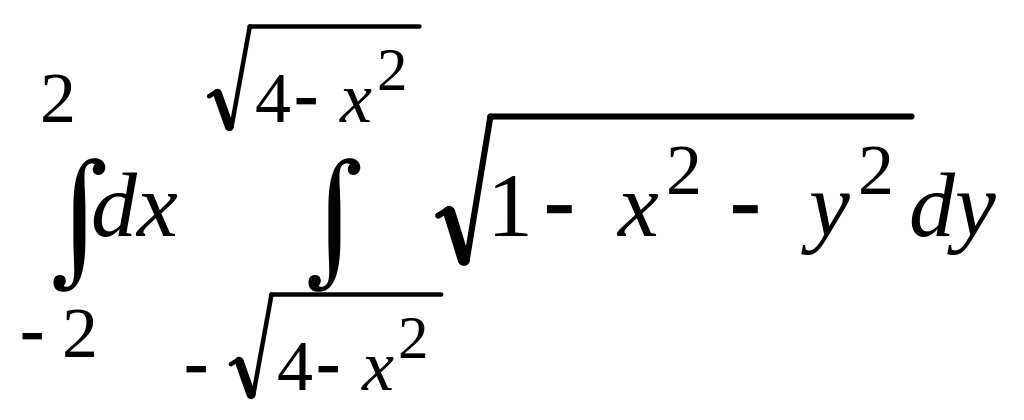 .
.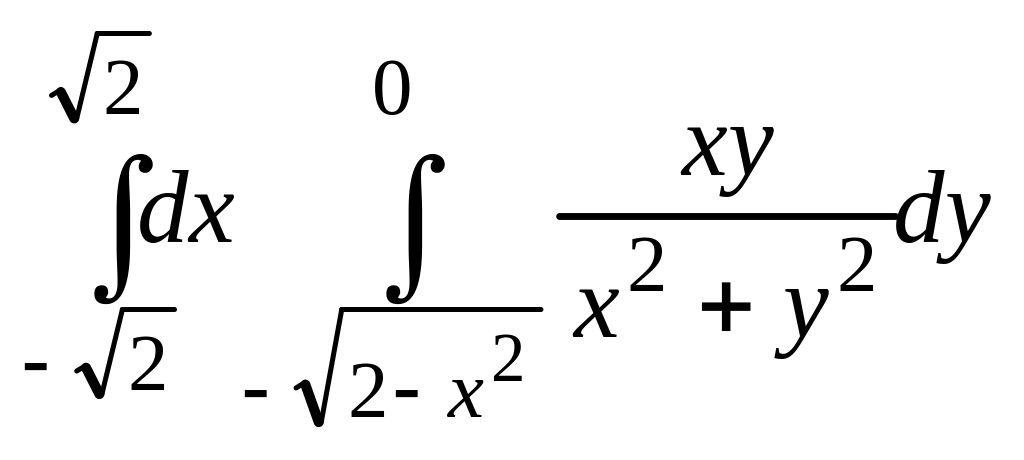
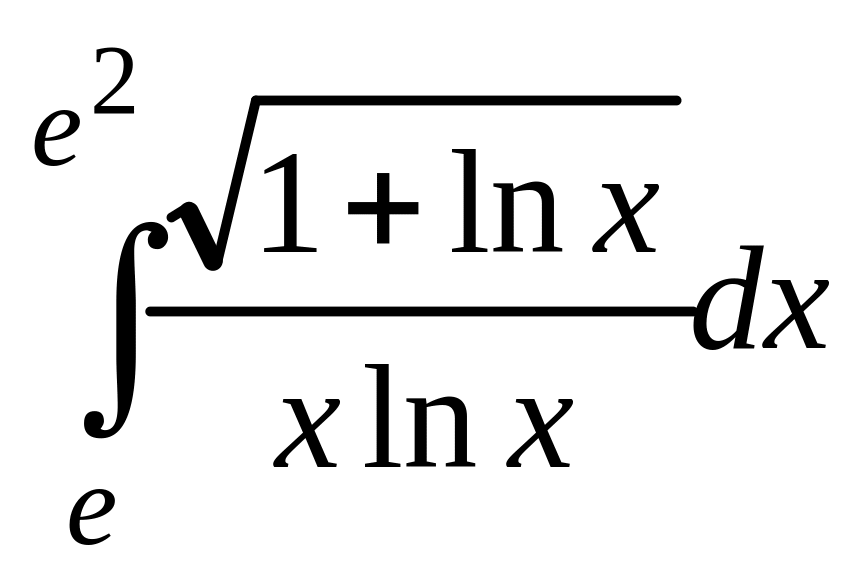 ;
;
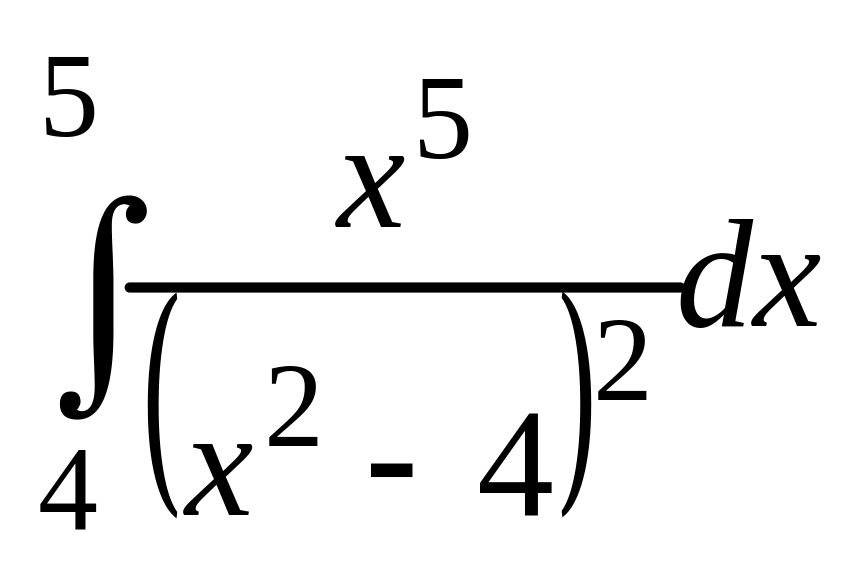 ;
;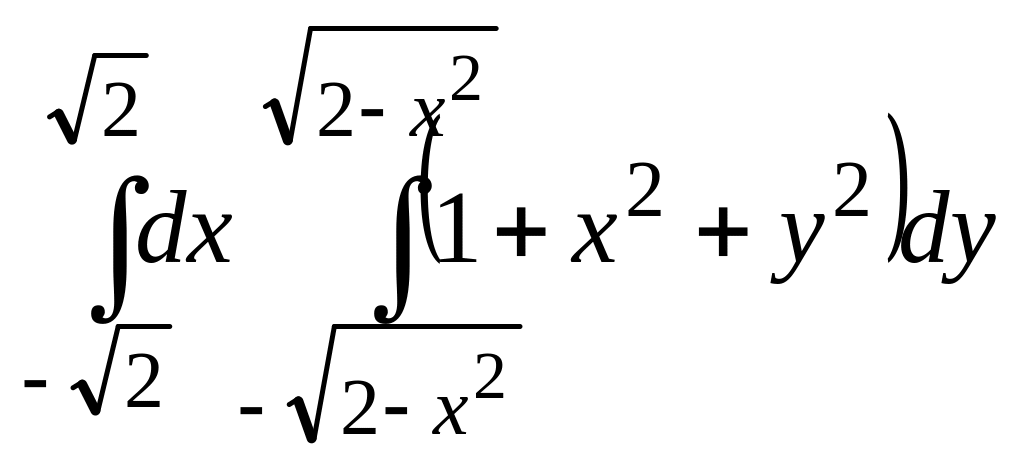
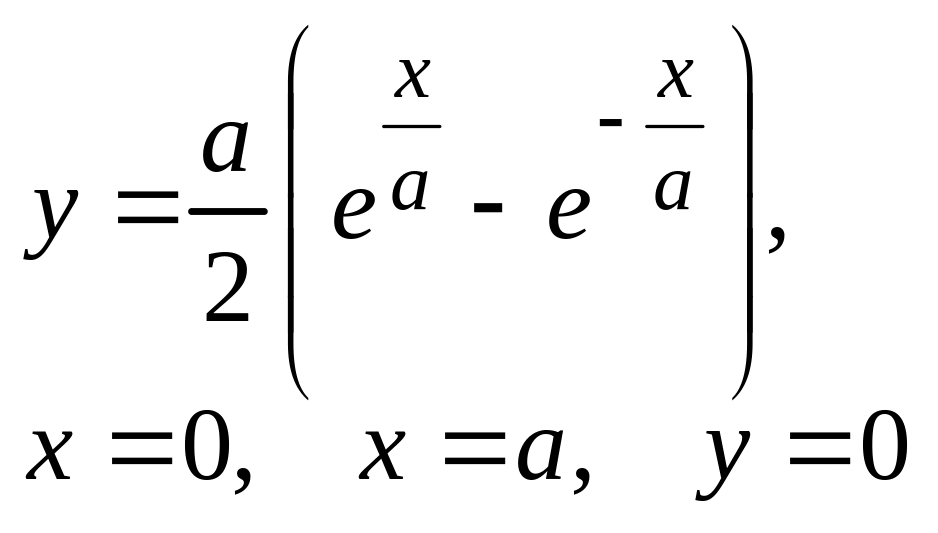
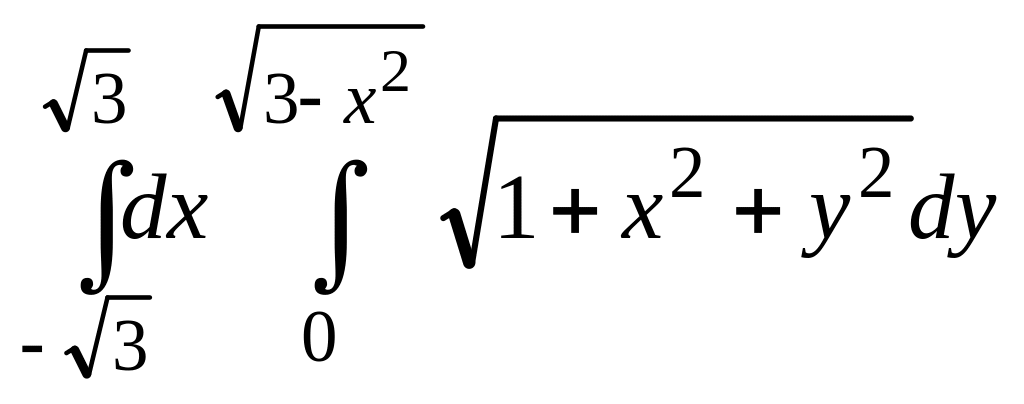

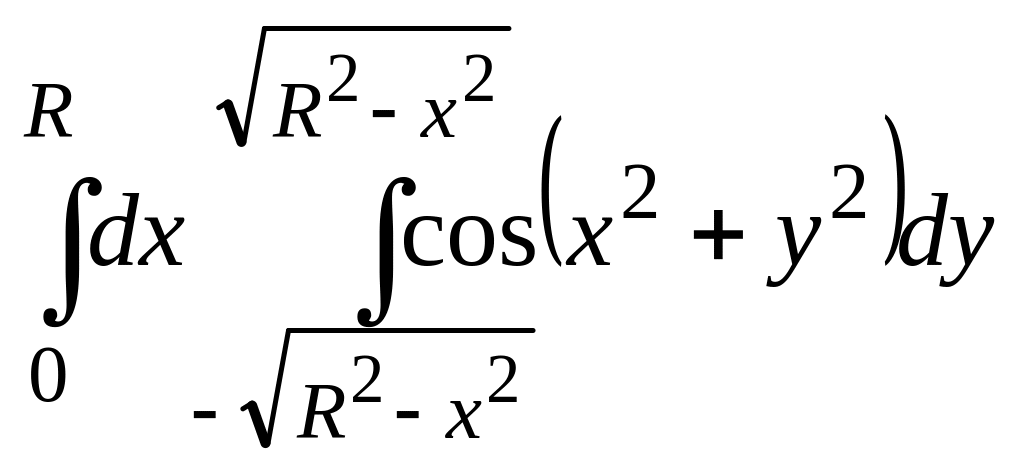
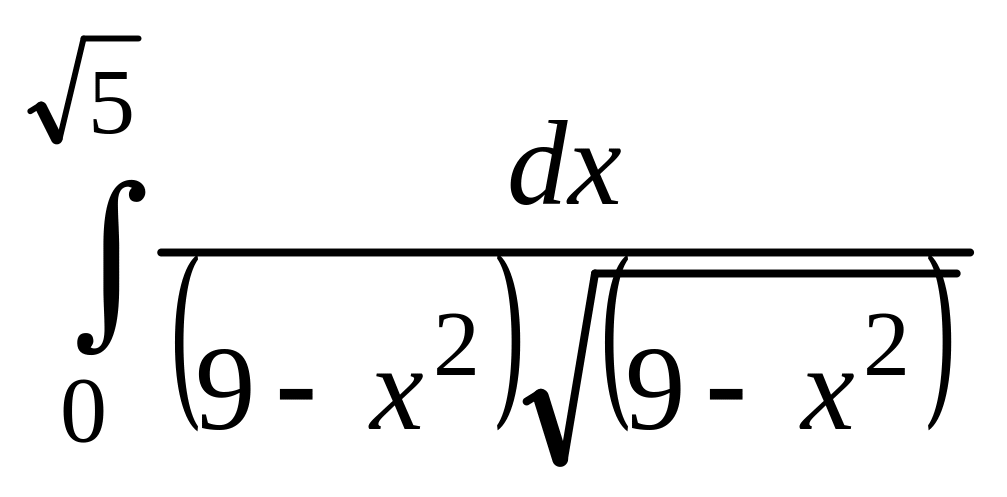 ;
;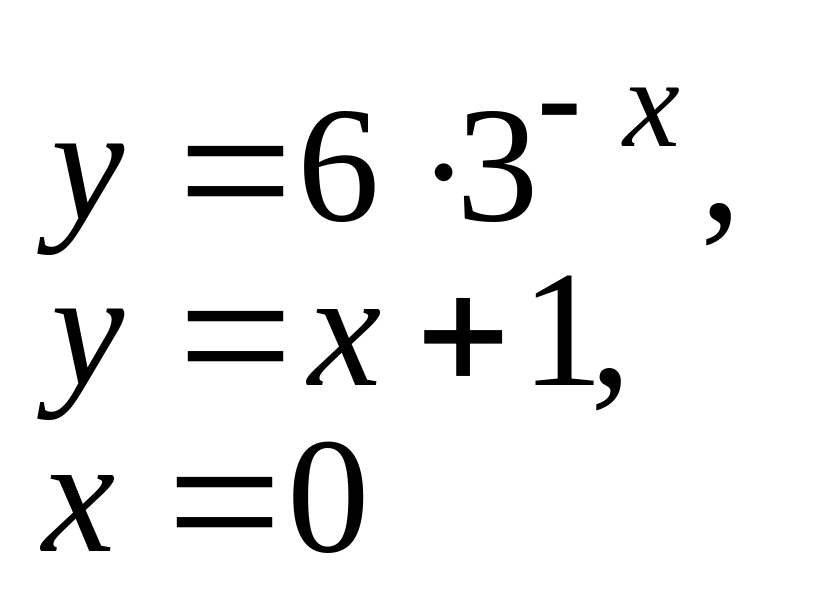
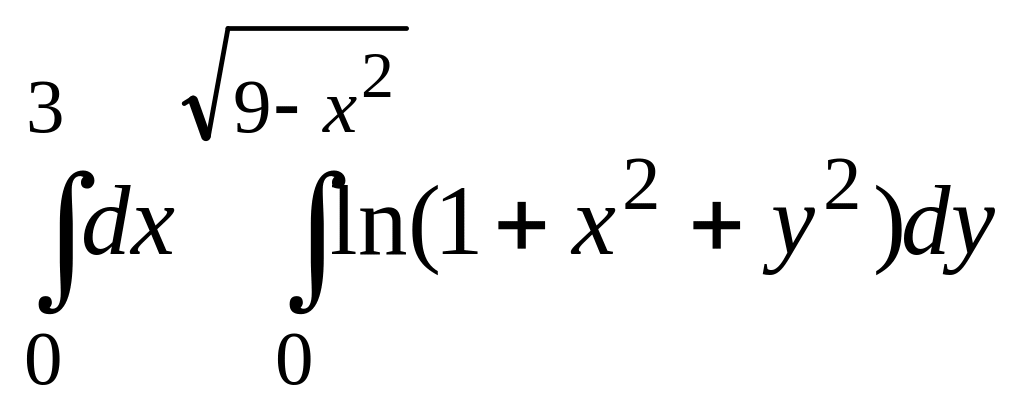 .
.