
- •В.В. Киричевський, н.М. Д’яченко інтегральне числення
- •6.050100 „Економічна кібернетика”
- •1. Неозначений інтеграл
- •1.1. Первісна і неозначений інтеграл
- •1.1.1. Основні властивості неозначеного інтегралу.
- •1.1.2. Таблиця основних інтегралів.
- •1.2. Основні методи інтегрування
- •1.2.1. Безпосереднє інтегрування.
- •1.2.2. Метод підстановки.
- •1.2.2.1. Частковий випадок: метод інтегрування внесення під диференціал.
- •1.2.2.2. Загальний випадок.
- •1.2.3. Інтегрування частинами.
- •1.3. Інтегрування раціональних функцій
- •1.4. Інтегрування тригонометричних функцій
- •1.5. Інтегрування ірраціональних функцій
- •2. Означений інтеграл
- •Поняття означеного інтегралу Римана та його властивості. Геометричний зміст означеного інтегралу
- •2.2. Економічний зміст означеного інтегралу
- •2.3. Обчислення означених інтегралів.
- •3. Застосування означеного інтегралу
- •3.1. Застосування означеного інтегралу в геометрії
- •3.1.1. Обчислення площ плоских фігур.
- •3.1.2. Обчислення довжин плоских дуг
- •3.1.3. Обчислення об’ємів тіл обертання
- •3.2. Застосування означеного інтегралу в економіці
- •4. Невласні інтеграли
- •5. Узагальнення поняття інтегралу
- •5.1. Визначення подвійного інтегралу та його властивості
- •5.2. Обчислення подвійних інтегралів
- •5.3. Геометричний зміст подвійного інтегралу
- •Типове індивідуальне завдання
- •Список літератури
- •Питання, що виносяться на самостійне вивчення
- •Питання, що виносяться на іспит і на колоквіум
- •Інтегральне числення
- •6.050100 „Економічна кібернетика”
5. Узагальнення поняття інтегралу
5.1. Визначення подвійного інтегралу та його властивості
Подвійний
інтеграл на прямокутнику.
Прямокутник
![]() розбивається прямими, паралельними
осям координат
розбивається прямими, паралельними
осям координат
![]() ,
,
![]() на
на
![]() часткових прямокутника
часткових прямокутника
![]()
![]() ,
,
![]()
![]() .
Вказане розбиття прямокутника позначимо
через
.
На кожному з часткових
прямокутників оберемо довільну точку
.
Вказане розбиття прямокутника позначимо
через
.
На кожному з часткових
прямокутників оберемо довільну точку
![]() .
Покладемо
.
Покладемо
![]() .
Довжину діагоналі прямокутника
,
що дорівнює
.
Довжину діагоналі прямокутника
,
що дорівнює
![]() назвемо діаметром прямокутника, а
найбільший із діаметрів усіх часткових
прямокутників
називається діаметром розбиття
прямокутника
і позначається
назвемо діаметром прямокутника, а
найбільший із діаметрів усіх часткових
прямокутників
називається діаметром розбиття
прямокутника
і позначається
![]() ,
тобто
,
тобто
![]() .
.
Число
![]() називається інтегральною
сумою
функції
називається інтегральною
сумою
функції
![]() ,
що відповідає даному розбиттю
прямокутника
і даному вибору проміжних точок
на частинних прямокутниках розбиття
.
,
що відповідає даному розбиттю
прямокутника
і даному вибору проміжних точок
на частинних прямокутниках розбиття
.
Якщо
існує скінченна границя
![]() ,
що не залежить ні від вибору розбиття
прямокутника
,
ні від виботу проміжних точок
на частинних прямокутниках розбиття
,
то функція
називається інтегрованою
на прямокутнику
,
а ця границя називається подвійним
інтегралом
і позначається
,
що не залежить ні від вибору розбиття
прямокутника
,
ні від виботу проміжних точок
на частинних прямокутниках розбиття
,
то функція
називається інтегрованою
на прямокутнику
,
а ця границя називається подвійним
інтегралом
і позначається
![]()
Подвійний
інтеграл по довільній області.
Нехай
- обмежена замкнена множина, що утворює
квадровану фігуру. Позначимо через
будь-який прямокутник, що містить в собі
область
.
Визначимо на цьому прямокутнику функцію
![]() .
Функцію
називають інтегрованою в області
,
якщо функція
.
Функцію
називають інтегрованою в області
,
якщо функція
![]() інтегрована в прямокутнику
.
Число
інтегрована в прямокутнику
.
Число
![]() назвемо подвійним інтегралом від функції
по області
і позначимо символом
назвемо подвійним інтегралом від функції
по області
і позначимо символом
![]() .
.
Мають місце багато спільних властивостей подвійного інтегралу функції двох змінних і означеного інтегралу функції однієї змінної:
необхідна умова інтегрованості функції: будь-яка інтегрована функція є обмеженою;
властивість лінійності інтегралу;
властивість адитивності, яка дещо відрізняється від такої властивості одновимірного інтегралу, а саме: інтеграл по області
 дорівнює сумі інтегралів по квадровним
областям, на які розбито область
;
дорівнює сумі інтегралів по квадровним
областям, на які розбито область
;добуток і частка інтегрованих на функцій є інтегрованою на функцією (для частки в припущенні про те, що для функції знаменника виконано:
 );
);якщо дана функція
 інтегрована на
,
то функція
інтегрована на
,
то функція
 інтегрована
і має місце нерівність
інтегрована
і має місце нерівність
 ;
;якщо
 і
і
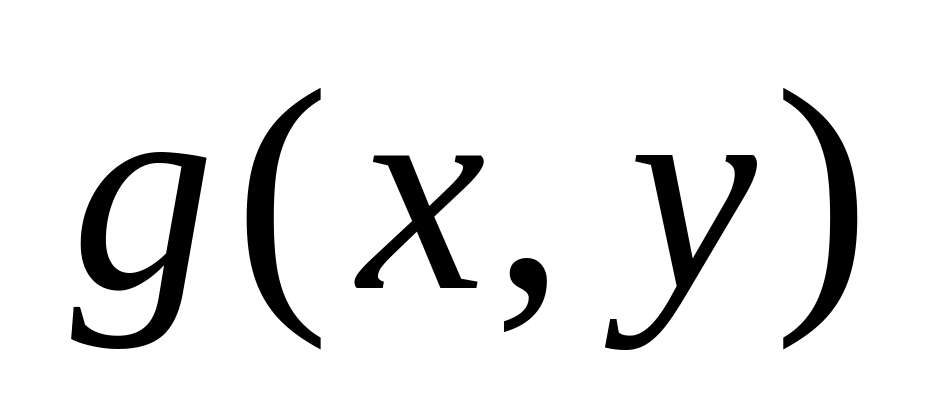 інтегровані на
і
інтегровані на
і
 на
,
то
на
,
то
![]() ;
;
зокрема,
якщо
![]() на
,
то
на
,
то
![]() ;
;
м
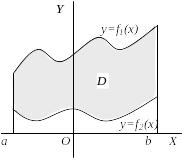
Рис. 5.1.
ає місце теорема про середнє: якщо неперервна на , то існує така точка ,
що
,
що
![]() .
.
5.2. Обчислення подвійних інтегралів
Якщо
![]() (рис. 5.1), де
(рис. 5.1), де
![]() неперервні на
функції, а
- інтегрована на
,
тоді подвійний
інтеграл виражається через повторний
співвідношенням:
неперервні на
функції, а
- інтегрована на
,
тоді подвійний
інтеграл виражається через повторний
співвідношенням:
|
|
(5.1) |
П
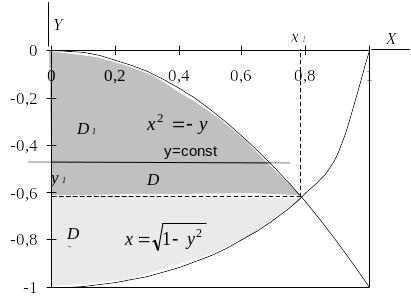
Рис. 5.2.
редставити подвійний інтеграл у вигляді повторного інтеграла з
зовнішнім інтегруванням за
у вигляді повторного інтеграла з
зовнішнім інтегруванням за
 та зовнішнім інтегруванням за
та зовнішнім інтегруванням за
 ,
якщо область
задана указаними лініями
,
якщо область
задана указаними лініями
![]() .
.
Рисунок області зображено на рис. 5.2. Спочатку знайдемо точку перетину даних кривих:
![]()
![]()
![]()
![]()
![]() .
.
Представимо подвійний інтеграл у вигляді повторного інтеграла з зовнішнім інтегруванням за . В цьому випадку треба вказати незмінні межі інтегрування за , а межі інтегрування за будуть функціями, що залежать від . Для цього потрібно
в рівняннях границі виразити через :
 ,
при цьому необхідно
врахувати, що в рівнянні першої кривої
перед коренем стоїть знак „+”, тому що
у даному випадку область обмежена
правою
гілкою параболи;
,
при цьому необхідно
врахувати, що в рівнянні першої кривої
перед коренем стоїть знак „+”, тому що
у даному випадку область обмежена
правою
гілкою параболи;провести прямі, паралельні вісі абсцис (тобто прямі
 )
з метою виявлення необхідності розбиття
області на частини, а саме:
)
з метою виявлення необхідності розбиття
області на частини, а саме:
якщо така пряма проходить вище прямої
 ,
то вона спочатку перетинає вісь ординат,
а потім криву
,
то вона спочатку перетинає вісь ординат,
а потім криву
 ,
,
якщо така пряма проходить нижче прямої , то вона спочатку перетинає вісь ординат, а потім криву
 ;
;
отримане означає, що дану область потрібно розбити на дві частини прямою ;
першій з отриманих областей
 відповідають такі зміни
і
:
відповідають такі зміни
і
:
![]() ,
,
![]() ,
,
другій з отриманих областей
 відповідають такі зміни
відповідають такі зміни
 і
:
і
:
![]() ,
,
![]() .
.
Розставляємо межі інтегрування з зовнішнім інтегруванням за :
 .
.
Представимо подвійний інтеграл у вигляді повторного інтеграла з зовнішнім інтегруванням за . В цьому випадку треба вказати незмінні межі інтегрування за , а межі інтегрування за будуть функціями, що залежать від . Для цього потрібно
в рівняннях границі виразити через :
 ,
при цьому необхідно врахувати, що в
рівнянні другої кривої перед коренем
стоїть знак „‑”, тому що у даному
випадку область обмежена нижньою
частиною кола
,
при цьому необхідно врахувати, що в
рівнянні другої кривої перед коренем
стоїть знак „‑”, тому що у даному
випадку область обмежена нижньою
частиною кола
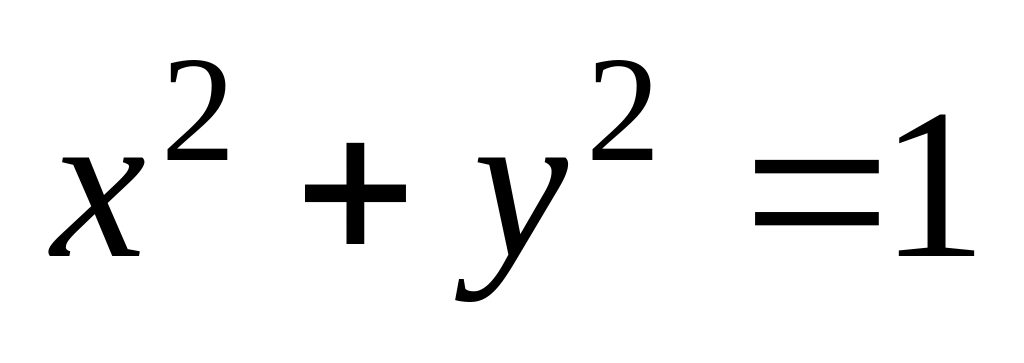 ,
,провести прямі, паралельні вісі ординат (тобто прямі
 )
з метою виявлення необхідності розбиття
області на частини, а саме: незалежно
від розташування такої прямої вона
спочатку перетинає криву
)
з метою виявлення необхідності розбиття
області на частини, а саме: незалежно
від розташування такої прямої вона
спочатку перетинає криву
 ,
а потім криву
,
а потім криву
 ,
тому у даному випадку розбивати область
на частини не потрібно,
,
тому у даному випадку розбивати область
на частини не потрібно,області відповідають такі зміни і :
![]() ,
,
![]() .
.
Розставляємо межі інтегрування з зовнішнім інтегруванням за :
 .
.
2. Обчислити подвійний інтеграл
![]()
Рисунок області інтегрування зображено на рис. 3.5. У даному випадку зручніше ставити зовнішню межу інтегрування – , щоб не розбивати область інтегрування на частини.
Виражаємо
через
в рівняннях кривих, отримаємо:
![]() .
Області
відповідають такі зміни
і
:
.
Області
відповідають такі зміни
і
:
![]() ,
,
![]() ,
тому
,
тому
![]()
![]()
![]()
![]()

Рис. 5.3.![]()
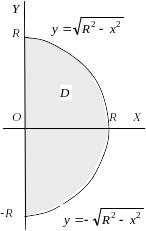
3. Обчислити подвійний інтеграл, використавши полярні координати
 .
.
Рисунок
області інтегрування зображено на рис.
5.3. Уведемо полярні координати
,
тоді
![]() ,
а рівняння кола
,
а рівняння кола
![]() ,
тобто
,
тобто
![]() в полярних координатах перепишеться,
як
в полярних координатах перепишеться,
як
![]() .
Тому область
.
Тому область
![]() перейде в область
,
якій відповідають зміни полярних
координат:
перейде в область
,
якій відповідають зміни полярних
координат:
![]() ,
,
![]() .
Тоді згідно до формули (5.1) отримаємо
.
Тоді згідно до формули (5.1) отримаємо



![]() .
.

 .
.