5.Поняття функції. Способи завдання функції та їх класифікація. Границя функції в точці за Гейне і за Коші та їх еквівалентність. Істотні границі

Поняття функції.

Означення. Нехай дана числова множина X a R, та кожному х є X поставлено у відповідь число у є R, тоді кажуть, що на множині X задана числова функція, и пишуть y = f(x), хєХ.

В цьому записі х називають аргументом або незалежною змінною, множину X називають областю визначення функції, її позначають також D( f ). Число у_{), що відповідає значенню аргументу х₍₎, називають значенням функції в точці х₀ і позначають f(x₀). Множину значень функції позначають інколи E( f).

Функції

називаються основними елементарними функціями.

Означення. Елементарною функцією називають функцію, яка може бути задана за допомогою скінченого числа арифметичних операцій і композицій з основних елементарних функцій.

Означений. Графіком функції у = fix) , х є D{ f), в прямокутній системі координат Ох у називають множину усіх точок площини с координатами (x;f(x)), х є D( f).

Означення . Функцію у = fix), задану на симетричній відносно нуля множині X, називають парною (непарною), якщо для кожного хєХ виконується рівність f(-x)=f(x), (f(-x)=-f(x)).

Графік парної функції симетричний відносно осі ординат, ірафік непарної функції симетричний відносно начала координат.

Означення. Число Т = 0 називають періодом функції y = f(x), якщо для будь-якого х € D(f) виконується:

х + Т є D(f), х - Т є D(f) , f(x + Т)= f(x).

Функцію, що має період називають періодичною. Графік періодичної функції при зсуву вздовж осі Ох на період переходить у себе.

Означення. Функцію у = f(x) називають обмеженою зверху(знизу) на множині

X D{ f), якщо існує С є R для будь якого Y є X виконується Означення. Функцію обмежену зверху і знизу на множині X називають обмеженою на множині X . Це еквівалентно такому: існує С > 0 для будь якого х є X =>│ f(x)│ С.

Означення. Функцію у = f(x) називають не зростаючою (не спадною) на множині X D( f), якщо . Якщо нерівності , строгі то функцію називають строго спадною та зростаючою відповідно.

Границя функції

Означении 1. (по Коші). Число b називається границею функції в точці а, якщо таке,що

Означення 2.(по Гейне). Число b називається границею функції в точці а, якщо для будь-якої збіжної до а послідовності такої, що , відповідно послідовність значень функції збігається до b.

Пишуть:

Теорема 1 . Означення 1 і 2 еквівалентні.

Теорема 2. Нехай функції задані в деякому околі точки а, окрім, можливо, самої точки а, і . Тоді:

Теорема 3. Нехай функції задані в деякому околі точки а, окрім,можливо,самої точки а, і задовольняють нерівностям . Нехай . Тоді .

Способы задания функции

Функцией называется закон, по которому числу х из заданного множества X, поставлено в соответствие только одно число у, пишут , при этом x называют аргументом функции, y называют значением функции. Существуют разные способы задания функций. 1. Аналитический способ. Аналитический способ - это наиболее часто встречающийся способ задания функции. Заключается он в том, что функция задается формулой, устанавливающей, какие операции нужно произвести над x, чтобы найти у.

Например: . Рассмотрим первый пример - . Здесь значению x = 1 соответствует , значению x = 3 соответствует и т. д. Функция может быть задана на разных частях множества X разными функциями. Например:

Во всех ранее приведенных примерах аналитического способа задания, функция была задана явно. То есть, справа стояла переменная y, а справа формула от переменной х. Однако, при аналитическом способе задания, функция может быть задана и неявно. Например: . Здесь, если мы задаем переменной x значение, то, чтобы найти значение переменной у (значение функции), мы должны решить уравнение. Например, для первой заданной функции при х = 3, будем решать уравнение:

. То есть, значение функции при х = 3 равно -4/3. При аналитическом способе задания, функция может быть задана параметрически - это, когда х и у выражены через некоторый параметр t. Например,

Здесь при t = 2, x = 2, y = 4. То есть, значение функции при х = 2 равно 4. 2. Графический способ. При графическом способе вводится прямоугольная система координат и в этой системе координат изображается множество точек с координатами (x,y). При этом . Пример: 3. Словесный способ. Функция задается с помощью словесной формулировки. Классический пример – функция Дирихле. «Функция равна 1, если х – рациональное число; функция равна 0, если х – иррациональное число». 4. Табличный способ. Табличный способ наиболее удобен, когда множество Х конечно. При этом способе составляется таблица, в которой каждому элементу из множества Х, ставится в соответствие число Y. Пример: Табличный способ задания функции очень удобен при обработке результатов исследований. Например, при выявлении зависимости между уровнем загрязнения окружающей среды и количеству людей, заболевших раком.

Істотні границі

Замеча́тельные преде́лы — термин, использующийся в советских и российских учебниках по математическому анализу для обозначения некоторых широко известных математических тождеств со взятием предела. Особенно известны:

• Первый замечательный предел:

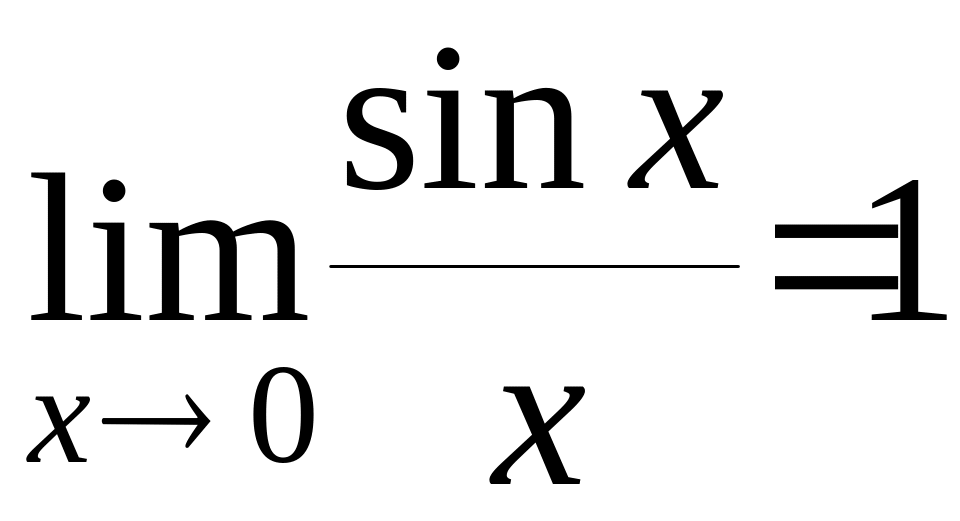
• Второй замечательный предел:

Следствия