39. Элипс, парабола, гипербола и их свойства.

Парабола- наз. такое мн-во точек в пл-ти для каждой из которых расстояние до заданной точки пл-ти М фокуса = расстоянию от этой точки до заданной прямой (директриса). Расстояние р от фокуса до директрисы наз. фокальным параметром параболы. Прямая директрисе и проходящая через фокус наз. осью параболы. Расстояние r от точки М до фокуса наз.фокальным радиусом этой точки. Точка пресечения параболы с ее осью наз. вершиной параболы. Каноническое ур-е пар.: . Свойства параболы: 1) ось параболы явл. осью симметрии; 2) Вершина параболы имеет корд. (0,0); 3) парабола явл. неограниченной кривой; 4) Ур-е дисектрисы параб. таково: .

Эллипсом – наз. такое мн-во точек пл-ти рнастояние от каждой точки которого до 2-х заданных точек пл-ти (фокуса) есть величина постоянная равная заданному числу 2a. Расстояние между фокусами наз. фокусным расстоянием эллипса, обозначают через 2с. Середина отрезка наз. центром эллипса. Длины отрезков наз. фокальными радиусами т. М. Прямая кот. проходит через точки наз. осью эллипса. Прямая, кот. проходит через центр эллипса наз. нефокальной осью эллипса. Рисунок 1.

Вывод канонического ур-я эллипса. Сначала декарт. сис-му координат выберем в центре эллипса, ось х направим вдоль оси эл. В направлении вектора . Ось y направим вдоль нефокальной оси эллипса, так чтобы система коорд. была правой. Пусть - произвольная точка эллипса. Согласно опред. эллипса . Упростим это уравнение: .

.

Поскольку a >c, то это дает право обозначить . Мы получим . Разделим обе части на прийдем к каноническому ур-ю эллипса: , здесь . Рисунок 2.

Св-ва эллипса: 1) Эллипс – ограниченная кривая расположенная в прямоугольнике со сторонами ; 2) Точка О(0,0) явл. центром симметрии эллипса (центр эллипса). 3) Ось эллипса и нефокальная ось явл. осями симметрии эллипса. Отношение наз. эксцентриситет эллипса. Директрисами эллипса наз. 2-е прямые || малой оси и стоящие от нее на расстоянии , ур-е дисектрисы имеет вид .

Гиперболой наз. мн-во точек пл-ти для каждой из кот. модуль разности расстояния до 2-х зад. точек пл-ти есть величина постоянная =2а. Каноническое ур-е гиперболы: . Св-ва гиперболы: 1) гипербола не ограниченная кривая; 2) Точка (0,0) явл. центром симметрии гиперболы ; 3) фокальные и нефокальные оси гиперболы явл. осями симметрии. Прямые наз. асимптотами гпп. -эксцинтриситет. - директриса гиперболы.

40. Приведение линии 2-го порядка к каноническому виду

Линии второго порядка, плоские линии, декартовы прямоугольные координаты которых удовлетворяют алгебраическому уравнению 2-й степени .(*)

Уравнение (*) может и не определять действительного геометрического образа, но для сохранения общности в таких случаях говорят, что оно определяет мнимую Л. в. п. В зависимости от значений коэффициентов общего уравнения (*) оно может быть преобразовано с помощью параллельного переноса начала и поворота системы координат на некоторый угол к одному из 9 приведённых ниже канонических видов, каждому из которых соответствует определённый класс линий.

Кривая 2–го порядка, определяемая уравнением (*), принадлежит к одному из следующих типов: эллипс; гипербола; парабола; пара прямых (пересекающихся, параллельных или совпадающих); точка; пустое множество.

Приведение уравнения второго порядка к каноническому виду.

Определение 11.9. Линия, определяемая общим уравнением второго порядка

, (11.5)

называется алгебраической линией второго порядка.

Для квадратичной формы можно задать матрицу

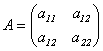. (11.6)

Для того, чтобы перейти к новой системе координат, в которой уравнение линии будет иметь канонический вид, необходимо провести два преобразования:

1) поворот координатных осей на такой угол, чтобы их направление совпало с направлением осей симметрии кривой (если она имеет две оси);

2) параллельный перенос, при котором начало координат совмещается с центром симметрии кривой (если он существует).

Замечание. Для параболы новые оси координат должны располагаться параллельно и перпендикулярно директрисе, а начало координат – совпасть с вершиной параболы.

Поскольку в канонических уравнениях кривых второго порядка отсутствуют произведения переменных, необходимо перейти к координатной системе, определяемой базисом из ортонормированных собственных векторов матрицы А. В этом базисе уравнение (11.5) примет вид:

(в предположении, что λ_1,2 не равны 0).

Зададим последующий параллельный перенос формулами:

. Получим в новой координатной системе уравнение

. (11.7)

Рассмотрим возможные геометрические образы, определяемые этим уравнением в зависимости от знаков λ₁, λ₂ и :

1)       если собственные числа матрицы А λ₁ и λ₂ и одного знака, уравнение (11.7) представляет собой каноническое уравнение эллипса:

, где

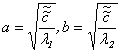
(случаи и , имеющего знак, противоположный знаку λ₁, λ₂, будут рассмотрены в следующей лекции).

2)если λ₁ и λ₂ имеют разные знаки, уравнение (11.7) является каноническим уравнением гиперболы:

или , в зависимости от знака .

В случае, когда одно из собственных чисел матрицы А равно 0, уравнение (11.5) в результате двух преобразований координат можно привести к виду:

, (11.8)являющимся каноническим уравнением параболы.