26. Скалярне та векторне поле та їх характеристики (градієнт скалярного поля, дивергенція і ротор векторного поля та ін.). Формули Грина, Остроградського-Гауса та Стокса.
def: Будемо
казати, що в області
є
заданим скалярним
(векторним) полем, якщо кожній точці
співставляє за деяким законом єдине
число (вектор). Іншими словами скалярне
(векторне) поле, це скалярна (векторна)
ф-ція задана в обл-ті D.
def: Скалярне поле U(M) називається диференційованим в точці , якщо його повний приріст можна представити у вигляді
,
де
,
,
- числа, що не залежать від
,
Еквівалентними є представлення повного приросту у вигляді:
,
.
Нехай
Тоді повний приріст матиме вигляд:
.
Знаючи
.
Означення градієнта
не залежить від вибору системи координат,
тому градієнт – це інваріант. Якщо
- одиничний вектор, що задає напрям, то
похідна скалярної функції за напрямом
обчислюється за формулою:
.
def:
Векторне поле
наз-ся
диференційованим в точі
існує
лінійний оператор А:
,
такий що
,
де
,
– вектор:
.
def: Векторне поле називається диференційованим в області D , якщо воно диференційовне в усіх точках області D.
def:
Похідна векторного поля
за напрямком
наз-ся
.
def:
Дивергенцією векторного поля, що є
диференційовним в точці М
наз-ся дивергенція оператора А,
що визначається умовою диференційовності
цього векторного поля в точці М.
Тобто, якщо
,
то
.
def: Ротор
визначається аналогічно, як
.
;
Формули обчислення похідної за напрямом:
,
де
- направляючі косинуси.
Формула Гріна.
Нехай
-
це площина в
,
-
одиничний
вектор нормалі до
,
D –
область на площині
.
D – однозв’язна плоска область, тобто будь-яка кусково-гладка зімкнена крива, що лежить в D обмежує область, яка також цілком лежить в D .
Умови на D:
1)
-
зімкнена, кусково гладка, без особливих
точок,
тут
-
межа області D,
тобто множина межових точок D
;
2) на площині π можна обрати таку декартову прямокутну систему координат, що усі прямі, які паралельні осям координат перетинають С не більш, ніж у двох точках.
Th
(формула
Гріна):
Нехай
-
векторне поле, диференційовне в області
D,
що задовольняє умовам 1) і 2);
-
має неперервні похідні за будь-яким
напрямком в точках об’єднання
.
Тоді виконується формула:
.
Формула
Остроградського-Гаусса.
-
однозв’язна
тривимірна область
- кусково-гладкої, зімкненої поверхні
такої, що
,
область D,
яку вона обмежує лежить всередині D,
тобто
.
-
множина межових точок області D.
Поверхня S в задовольняє умовам:
1) S – кусково-гладка, без особливих точок, двозв’язна, повна, обмежена, зімкнена;
2) Oxyz (можна обрати прямокутну систему координат), таку, що будь-яка пряма, паралельна координатній осі, перетинає S не більше, як двох точках.
-
одиничний вектор зовнішньої до поверхні
S
нормалі.
Th
(формула
Остроградського-Гаусса).
Нехай
- векторне поле, диференційовне в D,
яке задовольняє умовам 1) і 2) і, крім
того, похідна за будь-яким напрямом
неперервна в
.
Тоді здійснюється формула
Формула Стокса.
d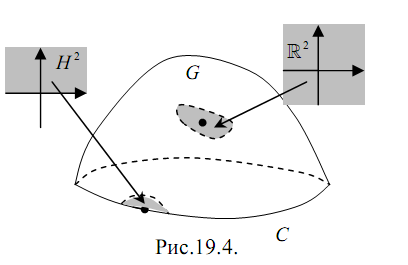
ef:
Поверхнею
з краєм
називається така множина G,
деякий окіл кожної з точок якої є
гомеоморфним образом або множини
або
.
Множина С
тих точок, околи яких є гомеоморфними
образами множини
,
називається краєм
поверхні
G
(див.рис.19.4).
Умови на поверхню S:
1) S – кусково-гладка, без особливих точок, двостороння, повна, обмежена,
2)∃ С - край поверхні S, який є кусково-гладкою, без особливих точок просторовою кривою;
3)∃ система координат Oxyz така, що поверхня S однозначно проектуємо на кожну з трьох координатних площин.
- одиничні вектори нормалі
до S.
-
одиничний вектор дотичної в точці
контура С
з напрямом, що узгоджено з
(правило «штопора»).
З цих вимог виконується Th(ма).
Th (формула Стокса): Якщо - векторне поле, неперервно диференційовне в околі поверхні S (у відкритій множині, що містить у собі S), поверхня S задовольняє зазначеним умовам, тоді здійснюється формула
.